AHP层次分析法python实现

问题背景描述
某高校正在进行教师的评优工作，现应用层次分析法对待评教师的综合素质进行评价。整个层次结构分为三层，最高层即问题分析的总目标，要评选出优秀教师A；第二层是准则层，包括三种指标学识水平C1、科研能力C2、教学工作C3；第三层是方案层，即参加评优的教师，假设对五位候选教师P1、P2、P3、P4、P5进行评优，其中P2、P3、P4为任课教师，需要从学识水平、科研能力、教学工作三方面评估其综合素质，教师P5是科研人员，只需从学识水平、科研能力两方面衡量其综合素质，教师P1是行政人员，只需从学识水平和教学工作两方面衡量。
三个评价指标的相对重要程度不同，并且各位教师在三个指标上表现不同，具体如下：科研能力指标比学识水平指标明显重要，教学工作指标比学识水平指标稍微重要，科研能力指标比教学工作指标稍微重要。在学识水平上，P1稍微高于P2，P1明显高于P3，P1比P4处于稍微高与明显高之间，P1强烈高于P5，P2稍微高于P3，P2比P4处于同样高与稍微高之间，P2明显高于P5，P3比P5处于同样高与稍微高之间，P4比P3处于同样高与稍微高之间，P4稍微高于P5；在科研能力上，P3强烈高于P2，P4稍微高于P2，P5明显高于P2，P3明显高于P4，P3比P5处于同样高与稍微高之间，P5稍微高于P4；在教学工作上，P1稍微高于P3，P1稍微高于P4，P2稍微高于P3，P2稍微高于P4，P1与P2水平相当，P3与P4水平相当。

import numpy as np  # Python本身没有处理矩阵的数据类型，因此需要使用附加的函数库。

"""
1. 读取csv文件
"""


def prin(path):
    tmp = np.loadtxt(path, dtype=np.str, delimiter=",")
    tmp = tmp.astype(float)  # 类型转换
    return tmp


"""
2. 方根法求单层元素相对重要性
"""


def ReImpo(F):
    n = np.shape(F)[0]  # F矩阵的行数，np.shape(F)[1]为列数
    W = np.zeros([1, n])  # 生成1行n列的0矩阵
    for i in range(n):
        t = 1
        for j in range(n):
            t = F[i, j] * t  # 累乘
        W[0, i] = t ** (1 / n)  # 开n次方根求Wi
    W = W / sum(W[0, :])  # 归一化
    return W.T


"""
3. 一致性检验
"""


def isConsist(F, RI):
    n = np.shape(F)[0]  # F矩阵的行数，np.shape(F)[1]为列数
    W = np.zeros([1, n])
    λmi = np.zeros([1, n])
    λmax = 0
    for i in range(n):
        t = 1
        for j in range(n):
            t = F[i, j] * t  # 累乘
        W[0, i] = t ** (1 / n)  # 开n次方根求Wi
    for i in range(n):
        temp = 0
        for j in range(n):
            temp = F[i, j] * W[0, j] + temp
        λmi[0, i] = temp / W[0, i]
        λmax = λmax + λmi[0, i] / n
    CI = (λmax - n) / (n - 1)
    CR = CI / RI
    if CR <= 0.1:
        return bool(1)
    else:
        return bool(0)


"""
4. 计算综合重要性
"""


def ComImpo(F12, F231, F232, F233):  # 综合重要性
    if isConsist(F12, 0.58) and isConsist(F231, 1.12) and isConsist(F232, 0.90) and isConsist(F233, 0.90):
        W12 = ReImpo(F12)
        W231 = ReImpo(F231)
        b = np.array([[0]])
        W232 = np.r_[b, ReImpo(F232)]  # np.r_是按列连接两个矩阵
        W233 = np.r_[ReImpo(F233), b]
        W23 = np.hstack([W231, W232, W233])  # np.hstack将参数元组的元素数组按水平方向进行叠加
    else:
        print("判断矩阵不通过一致性检验！")
        return 0
    n = len(W23)
    C = np.zeros([1, n])
    for i in range(n):
        t = W23[i, :]
        C[0, i] = sum((W12.T * t)[0])
    return C


def main():
    F1 = prin("F1.csv")
    F2 = prin("F2.csv")
    F3 = prin("F3.csv")
    F4 = prin("F4.csv")
    C = ComImpo(F1, F2, F3, F4)
    print("P1-P5五位教师综合推荐指数分别为：")
    for i in range(5):
        print(C[0, i])
    print("因此评价排序为：")
    print(np.argsort(-C) + 1)  # 将C中的元素从大到小排列，提取其对应的index(索引)


if __name__ == '__main__':
    main()

相对于总目标各指标间的相对重要性（三阶判断矩阵）

各教师的学识水平比较（五阶判断矩阵）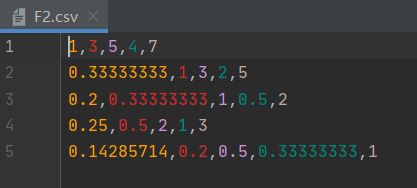
各教师的科研能力比较（四阶判断矩阵）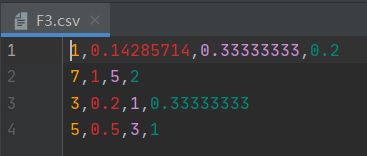
各教师的教学工作比较（四阶判断矩阵）
运行结果

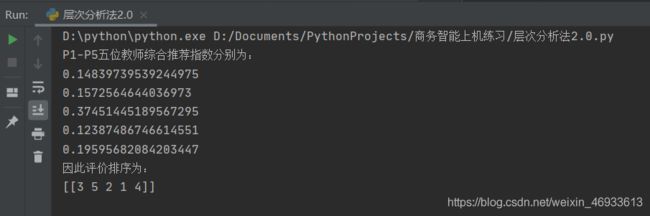
实验结果表明，对P1-P5五位教师综合素质进行评价排序由高到低为：P3,P5,P2,P1,P4。