python插值与拟合
由这张图我们粗略的了解插值和拟合:下面正式介绍。
一维插值
一维插值就是在已知互不相同的观测点![]() 除的函数值:寻找一个近似函数
除的函数值:寻找一个近似函数![]() 使得
使得![]() ,也就是这个函数的曲线要通过所有观测点。这样我们就能观测
,也就是这个函数的曲线要通过所有观测点。这样我们就能观测![]() 在非观测点
在非观测点![]() 之外的点的函数值。
之外的点的函数值。
![]() 称为插值函数,含
称为插值函数,含![]() (i=0,1,,,n)的最小区间[a,b]称作插值区间,
(i=0,1,,,n)的最小区间[a,b]称作插值区间,![]() 称作插值点。
称作插值点。
注意:插值方法一般用于插值区间内部点的函数值估计或者预测,当大于预测区间时,通常我们也可以进行短期的预测,对于中长区是不可取的。这也就告诉我们插值方法可以对数据中缺失的数据进行填补。
多项式插值
![]() (i=0,1,2,,n),这个插值条件式子共有
(i=0,1,2,,n),这个插值条件式子共有![]() 个约束方程,而n次多项式也恰好有n+1个待定系数法。如果已知这些函数点以及函数值,我们可以确定一个次数不超过n的多项式。
个约束方程,而n次多项式也恰好有n+1个待定系数法。如果已知这些函数点以及函数值,我们可以确定一个次数不超过n的多项式。
![]() ,这个多项式满足
,这个多项式满足![]() 。
。
对于上面多项式系数通常可以用三种方法;待定系数法,拉格朗日插值,牛顿插值。
这里我们介绍前两种方法,因为根据克莱姆法则方程的解唯一,所以三种插值方法的计算结果相同,掌握一种即可。
待定系数法
将已知的函数点和函数值代入多项式中:得到
我们将其写成矩阵的形式:
于是我们根据举证乘法可以得到这个系数的解:记系数矩阵为A,所以有![]()
引入几个例题;
已知函数的6个观测点,求插值函数![]() ,并求x=1.5,2.6的观测值。
,并求x=1.5,2.6的观测值。
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 16 | 18 | 21 | 17 | 15 | 12 |
import numpy as np
x0=np.arange(1,7)
y=np.array([16,18,21,17,15,12])
X=np.vander(x0)
a=np.linalg.inv(X)@y
print(a)
yh=np.polyval(a,[1.5,2.6])
print(yh)(1) 我们可以看出多项式中的X矩阵是一个标椎的范德蒙矩阵,所以我们使用numpy库里的内置函数构造一个范德蒙矩阵——vander
(2)我们在numpy中求逆函数的标准函数是np.linalg.inv()
(3)函数polyval(A,[m,n...]),A输入多项式系数值,列表中包含需要预测的函数点。
拉格朗日插值
原理不具体介绍,这里直接介绍在python的方法。还是以上面的例子为例。
import numpy as np
from scipy.interpolate import lagrange
x0=np.arange(1,7)
y=np.array([16,18,21,17,15,12])
a=lagrange(x0,y)
print(a)
yh=np.polyval(a,[1.5,2.6])
print(yh)输出以后的系数和用待定系数法求得的结果是一样的,预测方法也相同的。
但是我们在实际问题中很少使用多项式插值,因为多项式插值随着次数的增高,会产生龙格现象。(龙格现象指的是随着插值的次数增加,也就是插值点的增加,插值结果越偏离原函数。),所以我们通常使用分段线性插值和三次样条插值。
分段线性插值和三次样条插值
分段线性插值:简单来说就是每两个相邻的节点用直线相连,如此形成的一条直线就是分段线性插值函数,记作![]() ,并且同样满足
,并且同样满足![]() ,在每个小区间内是线性函数。这里简单介绍一下原理。
,在每个小区间内是线性函数。这里简单介绍一下原理。
三次样条插值:分段线性插值在连接点处的光滑程度不高,于是我们重新定义一个函数![]() ,这个函数满足(1)在每个小区间[x,x+1]上
,这个函数满足(1)在每个小区间[x,x+1]上![]() 是K次多项式。
是K次多项式。![]()
(2)![]() 在[a,b]上具有k-1阶连续导数
在[a,b]上具有k-1阶连续导数
具备这两个条件就称![]() 为关于划分
为关于划分![]() 的k次样条函数。而三次样条函数就是其中之一, 在每个小区间[x,x+1]上
的k次样条函数。而三次样条函数就是其中之一, 在每个小区间[x,x+1]上![]() 是三次多项式,
是三次多项式, ![]() 在[a,b]上具有2阶连续导数,并且在节点处有
在[a,b]上具有2阶连续导数,并且在节点处有![]() 。
。
话不多说直接上例题,原理我们稍作了解具体还是了解代码运作
先介绍我们使用的函数,scipy.interpolate模块有一维插值函数interp1d,二维插值函数interp2d.
interp1d基本的调用格式为interp1d(x,y,kind='linear'),kind取值是方法为字符串,指明了插值方法,默认为分段线性插值,'zero','slinear','quadratic','cubic'分别指的是0阶,一阶,二阶,三阶样条插值。
在区间[0,10]上取等间距1000个点![]() ,并计算这些点
,并计算这些点![]() 处函数
处函数![]() 的函数值
的函数值![]() 利用观测点,求三次样条插值函数。并且积分
利用观测点,求三次样条插值函数。并且积分![]() 和
和![]() 。
。
from scipy.interpolate import interp1d
from scipy.integrate import quad
import scipy as sp
import numpy as np
y=lambda x: (3*x**2+x*4+6)*np.sin(x)/(x**2+8*x+6)
x=np.linspace(0,10,1000)
y1=y(x)
y2=interp1d(x,y1,'cubic')
y3=y2(x)
I=quad(y,0,10)
print(I)
I2=np.trapz(y3,x)
print(I2)(1)对于进行插值的interp1d函数,我们已经介绍过,学会使用即可。
(2)对于有具体函数形式的方程,我们使用从 scipy.integrate导入的函数quad进行定积分处理,使用形式如下 quad(fun,n,m),fun中是具体的函数,剩余两个参数指的是从n到m的积分区域。对于使用插值预测的函数,我们通常使用numpy给出的函数trapz函数,trapz(y,x)函数中y指的是使用积分区域预测出的插值,x指的是积分区域。(通常x需要有多个插值点)
例题2
已知温度为T,T=[700,720,740,760,780] ,过热蒸汽体积的变化V=[0.0977,0.1218,0.1406,0.1551,0.1664],分别采用分段线性插值和三次样条插值求解T=[750,770]的体积变化,并在一个图形中画出这两个函数。
from scipy.interpolate import interp1d
import pylab as plt
import numpy as np
T=np.array([700,720,740,760,780])
V=np.array([0.0977,0.1218,0.1406,0.1551,0.1664])
s3=interp1d(T,V,'cubic')
s=interp1d(T,V)
x=[750,770]
y1=s3(x);print('三次样条预测=',y1)
y2=s(x);print('分段线性插值=',y2)
x=np.linspace(700,780,81)
y3=s3(x);y4=s(x)
plt.rc('font',family='SimHei')
plt.plot(x,y3,'*-',label='三次样条插值')
plt.plot(x,y4,'-',label='分段线性插值')
plt.legend()
plt.show()plt.rc('font',family='SimHei')这个语句做用是使中文能够正常显示,而plt.legend()是为了让标签显示,如果不明白可以去掉这个语句在查看图形。
二维插值
二维插值问题描述如下:给定的![]() 平面上有
平面上有![]() 个互不相同的插值节点,同时也已知这些插值节点处的观测值。求一个近似的二元插值曲面函数
个互不相同的插值节点,同时也已知这些插值节点处的观测值。求一个近似的二元插值曲面函数![]() ,使其通过全部已知节点即要求任一插值点
,使其通过全部已知节点即要求任一插值点![]() 处的函数值,可以利用插值函数进行预测。
处的函数值,可以利用插值函数进行预测。
二维插值常见的分为两种:网格节点插值和散乱数据插值
网格节点插值:用于规则矩形网格点插值情形。散乱数据插值:用于一般数据点,尤其是数据点杂乱无章的情况。
在python中对于网格节点插值我们使用interp2d函数,而对于散乱数据插值我们使用griddata函数,这两个函数均来自scipy.interpolate中,由于通常我们使用二维插值较少,所以再此不过多介绍。
拟合
已知一组二维数据,即平面上的n个点![]() ,要寻求一个函数(曲线)
,要寻求一个函数(曲线)![]() ,使
,使![]() 在某种准则下与所有数据点最为接近,也就是曲线拟合的最好,同时记
在某种准则下与所有数据点最为接近,也就是曲线拟合的最好,同时记![]() ,称
,称![]() 为拟合函数
为拟合函数![]() 在
在![]() 点出的残差。
点出的残差。
最小二乘拟合
前面介绍了残差的概念,为了使![]() 与其给定数据最接近,可以采用‘残差的平方和最小’作为评判标准,使得残差平方和最小。这一原则被称为最小二乘原则,根据最小二乘原则确定拟合函数
与其给定数据最接近,可以采用‘残差的平方和最小’作为评判标准,使得残差平方和最小。这一原则被称为最小二乘原则,根据最小二乘原则确定拟合函数![]() 的方法被称为最小二乘法。
的方法被称为最小二乘法。
通常,拟合函数是自变量![]() 和待定参数
和待定参数![]() 的函数,也就是
的函数,也就是![]() ,所以按照参数
,所以按照参数![]() 的线性与否,最小二乘法也分为线性最小二乘和非线性最小二乘。
的线性与否,最小二乘法也分为线性最小二乘和非线性最小二乘。
线性最小二乘
给定一个线性无关的函数系![]() ,如果拟合函数以其线性组合的形式
,如果拟合函数以其线性组合的形式
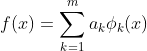 ,例如
,例如![]() ,则
,则![]() 就是关于参数
就是关于参数![]() 的线性函数,然后将式子
的线性函数,然后将式子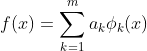 代入残差公式
代入残差公式 ,然后我们对系数求偏导,最终形成一个关于
,然后我们对系数求偏导,最终形成一个关于![]() 的线性方程组,称为正规方程组。记
的线性方程组,称为正规方程组。记
,
 ,
,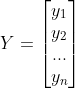 ,则正矩方程组可以表示为
,则正矩方程组可以表示为![]() ,那么我们可以算出
,那么我们可以算出![]() ,未所求拟合函数的系数。
,未所求拟合函数的系数。
非线性最小二乘法
对于给定的线性无关函数系![]() ,如果拟合函数不能以线性组合的形式出现例如:
,如果拟合函数不能以线性组合的形式出现例如:![]() ,
,![]() ,将表达式代入残差平方和中,形成了一个非线性函数极小化问题,可以使用非线性优化问题解出参数值。
,将表达式代入残差平方和中,形成了一个非线性函数极小化问题,可以使用非线性优化问题解出参数值。
值得注意的是拟合函数的选择非常重要,如果能根据问题的机理分析出变量之间的函数关系,那么只需要估计出相应参数即可,但是大多我们无法分析出问题的函数关系,所以最好先做出数据的散点图然后选择使用什么样的拟合函数。
一般来说数据分布接近曲线,适宜选用线性函数![]()
例题1:
利用下面的数据,根据最小二乘法建立p和q的之间的检验![]()
| p | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| q | 27.0 | 26.8 | 26.5 | 26.3 | 26.1 | 25.7 | 25.3 | 24.8 |
import numpy as np
T=np.arange(8)
y=np.array([27.0,26.8,26.5,26.3,26.1,25.7,25.3,24.8])
p=np.vstack([T,np.ones(8)]).T
a=np.linalg.pinv(p)@y
print(a)这里是将数据条件写成矩阵进行求解的,![]() 所以有
所以有![]() ,这里的函数np.linalg.pinv()是将非方阵矩阵求伪逆。np.vstack([T,np.ones(8)]).T指的是将函数垂直组合,.T的意义是将函数转置。
,这里的函数np.linalg.pinv()是将非方阵矩阵求伪逆。np.vstack([T,np.ones(8)]).T指的是将函数垂直组合,.T的意义是将函数转置。
当我们拟合的函数形式为多项式时,我们可以使用polyfit函数进行拟合,调用格式为polyfit(x,y,n),拟合n次多项式,返回的系数从高次到低次幂。
以刚才的例题为例
import numpy as np
T=np.arange(8)
y=np.array([27.0,26.8,26.5,26.3,26.1,25.7,25.3,24.8])
a=np.polyfit(T,y,1)
print(a)得到的结果和上面代码的结果几乎相同。
非线性拟合在python中一般我们使用scipy.optimize模块中的函数curve_fit,leastsq,least_squares等函数。这里我们介绍curve_fit()函数的用法。
调用格式为curve_fit(func,xdata,ydata),func为拟合的函数,xdata是自变量观测值,ydata是函数的观测值。会返回两个参数,第一个参数是拟合参数,第二个参数是数据的协方差矩阵。
例题,使用下面的数据拟合函数![]() ,x=[6,2,6,7,4,2,5,9],y=[4,9,5,3,8,5,8,2],z=[5,2,1,9,7,4,3,3]
,x=[6,2,6,7,4,2,5,9],y=[4,9,5,3,8,5,8,2],z=[5,2,1,9,7,4,3,3]
import numpy as np
from scipy.optimize import curve_fit
xy=np.array([[6,2,6,7,4,2,5,9],[4,9,5,3,8,5,8,2]])
z0=np.array([5,2,1,9,7,4,3,3])
z=lambda t,a,b,c: a*np.exp(b*t[0]) +c*t[1]**2
p,xov = curve_fit(z,xy,z0)
print(p)