《机器学习实战》9.3树回归之模型树和项目案例
《机器学习实战》9.3树回归之模型树和项目案例
搜索微信公众号:‘AI-ming3526’或者’计算机视觉这件小事’ 获取更多人工智能、机器学习干货
csdn:https://blog.csdn.net/baidu_31657889/
github:https://github.com/aimi-cn/AILearners
本文出现的所有代码,均可在github上下载,不妨来个Star把谢谢~:Github代码地址
一、引言
这一节我们来介绍模型树以及进行一个简单的树回归的项目实战
二、模型树
2.1 模型树简介
回归树的叶节点是常数值,而模型树的叶节点是一个回归方程。
用树来对数据建模,除了把叶节点简单地设定为常数值之外,还有一种方法是把叶节点设定为分段线性函数,这里所谓的 分段线性(piecewise linear) 是指模型由多个线性片段组成。
我们看一下图中的数据,如果使用两条直线拟合是否比使用一组常数来建模好呢?答案显而易见。可以设计两条分别从 0.0-0.3、从 0.3-1.0 的直线,于是就可以得到两个线性模型。因为数据集里的一部分数据(0.0-0.3)以某个线性模型建模,而另一部分数据(0.3-1.0)则以另一个线性模型建模,因此我们说采用了所谓的分段线性模型。
决策树相比于其他机器学习算法的优势之一在于结果更易理解。很显然,两条直线比很多节点组成一棵大树更容易解释。模型树的可解释性是它优于回归树的特点之一。另外,模型树也具有更高的预测准确度。
将之前的回归树的代码稍作修改,就可以在叶节点生成线性模型而不是常数值。下面将利用树生成算法对数据进行划分,且每份切分数据都能很容易被线性模型所表示。这个算法的关键在于误差的计算。
那么为了找到最佳切分,应该怎样计算误差呢?前面用于回归树的误差计算方法这里不能再用。稍加变化,对于给定的数据集,应该先用模型来对它进行拟合,然后计算真实的目标值与模型预测值间的差值。最后将这些差值的平方求和就得到了所需的误差。
2.2、模型树 代码
我们创建modelTree.py文件 编写代码如下
#!/usr/bin/env python
# -*- encoding: utf-8 -*-
'''
@File : modelTree.py
@Time : 2019/08/12 14:47:06
@Author : xiao ming
@Version : 1.0
@Contact : [email protected]
@Desc : None
@github : https://github.com/aimi-cn/AILearners
'''
# here put the import lib
from numpy import *
import numpy as np
import matplotlib.pyplot as plt
'''
@description: 根据特征切分数据集合
@param: dataSet - 数据集合
feature - 带切分的特征
value - 该特征的值
@return: mat0 - 切分的数据集合0
mat1 - 切分的数据集合1
'''
def binSplitDataSet(dataSet, feature, value):
mat0 = dataSet[np.nonzero(dataSet[:,feature] > value)[0],:]
mat1 = dataSet[np.nonzero(dataSet[:,feature] <= value)[0],:]
return mat0, mat1
'''
@description: 加载数据
@param: fileName - 文件名
@return: dataMat - 数据矩阵
'''
def loadDataSet(fileName):
dataMat = []
fr = open(fileName)
for line in fr.readlines():
curLine = line.strip().split('\t')
fltLine = list(map(float, curLine)) #转化为float类型
dataMat.append(fltLine)
return dataMat
'''
@description: 绘制ex00.txt数据集
@paramL filename - 文件名
@return: None
'''
def plotDataSet(filename):
dataMat = loadDataSet(filename) #加载数据集
n = len(dataMat) #数据个数
xcord = []; ycord = [] #样本点
for i in range(n):
xcord.append(dataMat[i][0]); ycord.append(dataMat[i][1]) #样本点
fig = plt.figure()
ax = fig.add_subplot(111) #添加subplot
ax.scatter(xcord, ycord, s = 20, c = 'blue',alpha = .5) #绘制样本点
plt.title('DataSet') #绘制title
plt.xlabel('X')
plt.show()
'''
@description: 生成叶结点
@param: dataSet - 数据集合
@return: 目标变量的均值
'''
def regLeaf(dataSet):
return np.mean(dataSet[:,-1])
'''
@description: 误差估计函数
@param: dataSet - 数据集合
@return: 目标变量的总方差
'''
def regErr(dataSet):
return np.var(dataSet[:,-1]) * np.shape(dataSet)[0]
'''
@description: 找到数据的最佳二元切分方式函数
@param: dataSet - 数据集合
leafType - 生成叶结点
regErr - 误差估计函数
ops - 用户定义的参数构成的元组
@return: bestIndex - 最佳切分特征
bestValue - 最佳特征值
'''
def chooseBestSplit(dataSet, leafType = regLeaf, errType = regErr, ops = (1,4)):
import types
#tolS允许的误差下降值,tolN切分的最少样本数
tolS = ops[0]; tolN = ops[1]
#如果当前所有值相等,则退出。(根据set的特性)
if len(set(dataSet[:,-1].T.tolist()[0])) == 1:
return None, leafType(dataSet)
#统计数据集合的行m和列n
m, n = shape(dataSet)
#默认最后一个特征为最佳切分特征,计算其误差估计
S = errType(dataSet)
#分别为最佳误差,最佳特征切分的索引值,最佳特征值
bestS = float('inf'); bestIndex = 0; bestValue = 0
#遍历所有特征列
for featIndex in range(n - 1):
#遍历所有特征值
for splitVal in set(dataSet[:,featIndex].T.A.tolist()[0]):
#根据特征和特征值切分数据集
mat0, mat1 = binSplitDataSet(dataSet, featIndex, splitVal)
#如果数据少于tolN,则退出
if (np.shape(mat0)[0] < tolN) or (np.shape(mat1)[0] < tolN): continue
#计算误差估计
newS = errType(mat0) + errType(mat1)
#如果误差估计更小,则更新特征索引值和特征值
if newS < bestS:
bestIndex = featIndex
bestValue = splitVal
bestS = newS
#如果误差减少不大则退出
if (S - bestS) < tolS:
return None, leafType(dataSet)
#根据最佳的切分特征和特征值切分数据集合
mat0, mat1 = binSplitDataSet(dataSet, bestIndex, bestValue)
#如果切分出的数据集很小则退出
if (np.shape(mat0)[0] < tolN) or (np.shape(mat1)[0] < tolN):
return None, leafType(dataSet)
#返回最佳切分特征和特征值
return bestIndex, bestValue
'''
@description: 树构建函数
@param: dataSet - 数据集合
leafType - 建立叶结点的函数
errType - 误差计算函数
ops - 包含树构建所有其他参数的元组
@return: retTree - 构建的回归树
'''
def createTree(dataSet, leafType = regLeaf, errType = regErr, ops = (1, 4)):
#选择最佳切分特征和特征值
feat, val = chooseBestSplit(dataSet, leafType, errType, ops)
#r如果没有特征,则返回特征值
if feat == None: return val
#回归树
retTree = {}
retTree['spInd'] = feat
retTree['spVal'] = val
#分成左数据集和右数据集
lSet, rSet = binSplitDataSet(dataSet, feat, val)
#创建左子树和右子树
retTree['left'] = createTree(lSet, leafType, errType, ops)
retTree['right'] = createTree(rSet, leafType, errType, ops)
return retTree
'''
@description: 绘制ex0.txt数据集
@paramL filename - 文件名
@return: None
'''
def plotDataSet1(filename):
dataMat = loadDataSet(filename) #加载数据集
n = len(dataMat) #数据个数
xcord = []; ycord = [] #样本点
for i in range(n):
xcord.append(dataMat[i][1]); ycord.append(dataMat[i][2]) #样本点
fig = plt.figure()
ax = fig.add_subplot(111) #添加subplot
ax.scatter(xcord, ycord, s = 20, c = 'blue',alpha = .5) #绘制样本点
plt.title('DataSet') #绘制title
plt.xlabel('X')
plt.show()
# 回归树测试案例
# 为了和 modelTreeEval() 保持一致,保留两个输入参数
def regTreeEval(model, inDat):
"""
Desc:
对 回归树 进行预测
Args:
model -- 指定模型,可选值为 回归树模型 或者 模型树模型,这里为回归树
inDat -- 输入的测试数据
Returns:
float(model) -- 将输入的模型数据转换为 浮点数 返回
"""
return float(model)
def modelLeaf(dataSet):
"""
Desc:
当数据不再需要切分的时候,生成叶节点的模型。
Args:
dataSet -- 输入数据集
Returns:
调用 linearSolve 函数,返回得到的 回归系数ws
"""
ws, X, Y = linearSolve(dataSet)
return ws
# 计算线性模型的误差值
def modelErr(dataSet):
"""
Desc:
在给定数据集上计算误差。
Args:
dataSet -- 输入数据集
Returns:
调用 linearSolve 函数,返回 yHat 和 Y 之间的平方误差。
"""
ws, X, Y = linearSolve(dataSet)
yHat = X * ws
# print corrcoef(yHat, Y, rowvar=0)
return sum(power(Y - yHat, 2))
# helper function used in two places
def linearSolve(dataSet):
"""
Desc:
将数据集格式化成目标变量Y和自变量X,执行简单的线性回归,得到ws
Args:
dataSet -- 输入数据
Returns:
ws -- 执行线性回归的回归系数
X -- 格式化自变量X
Y -- 格式化目标变量Y
"""
m, n = shape(dataSet)
# 产生一个关于1的矩阵
X = mat(ones((m, n)))
Y = mat(ones((m, 1)))
# X的0列为1,常数项,用于计算平衡误差
X[:, 1: n] = dataSet[:, 0: n-1]
Y = dataSet[:, -1]
# 转置矩阵*矩阵
xTx = X.T * X
# 如果矩阵的逆不存在,会造成程序异常
if linalg.det(xTx) == 0.0:
raise NameError('This matrix is singular, cannot do inverse,\ntry increasing the second value of ops')
# 最小二乘法求最优解: w0*1+w1*x1=y
ws = xTx.I * (X.T * Y)
return ws, X, Y
# 预测结果
def createForeCast(tree, testData, modelEval=regTreeEval):
"""
Desc:
调用 treeForeCast ,对特定模型的树进行预测,可以是 回归树 也可以是 模型树
Args:
tree -- 已经训练好的树的模型
testData -- 输入的测试数据
modelEval -- 预测的树的模型类型,可选值为 regTreeEval(回归树) 或 modelTreeEval(模型树),默认为回归树
Returns:
返回预测值矩阵
"""
m = len(testData)
yHat = mat(zeros((m, 1)))
# print yHat
for i in range(m):
yHat[i, 0] = treeForeCast(tree, mat(testData[i]), modelEval)
# print "yHat==>", yHat[i, 0]
return yHat
# 模型树测试案例
# 对输入数据进行格式化处理,在原数据矩阵上增加第0列,元素的值都是1,
# 也就是增加偏移值,和我们之前的简单线性回归是一个套路,增加一个偏移量
def modelTreeEval(model, inDat):
"""
Desc:
对 模型树 进行预测
Args:
model -- 输入模型,可选值为 回归树模型 或者 模型树模型,这里为模型树模型,实则为 回归系数
inDat -- 输入的测试数据
Returns:
float(X * model) -- 将测试数据乘以 回归系数 得到一个预测值 ,转化为 浮点数 返回
"""
n = shape(inDat)[1]
X = mat(ones((1, n+1)))
X[:, 1: n+1] = inDat
# print X, model
return float(X * model)
if __name__ == "__main__":
filename = 'C:\\Users\\Administrator\\Desktop\\blog\\github\\AILearners\\data\\ml\\jqxxsz\\9.RegTrees\\exp2.txt'
plotDataSet(filename)
对我们要进行处理的数据集进行查看~
数据集下载地址:数据集下载
用代码绘制数据集看一下:
我们可以看到和上面我们介绍的图像是一致的 我们就用代码使用模型树对其进行处理生成回归直线
生成模型树:
if __name__ == "__main__":
# 模型树
myDat = loadDataSet('C:\\Users\\Administrator\\Desktop\\blog\\github\\AILearners\\data\\ml\\jqxxsz\\9.RegTrees\\exp2.txt')
myMat = mat(myDat)
myTree2 = createTree(myMat, modelLeaf, modelErr, ops=(1, 20))
print(myTree2)
处理结果如下:
可以看到,该代码以0.285477为界创建了两个模板,原始图中实际是在0.3处分段,误差不大,createTree()生成的这个线性模型分别是y=3.468+1.1852x 和 y= 0.0016985+11.96477x,与用于生成该数据的真实模型非常接近。该数据实际是由模型y=3.5+1.0x 和 y=0+12x 在加上高斯噪声生成的。
我们可以看下拟合情况如下图:
可以看出来使用模型树来做出来的回归是不错的。
三、树回归项目案例
项目案例1: 树回归与标准回归的比较
3.1、项目概述
前面介绍了模型树、回归树和一般的回归方法,下面测试一下哪个模型最好。
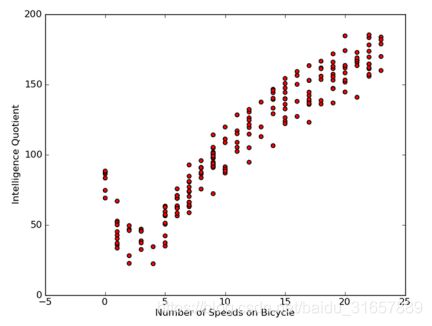
这些模型将在某个数据上进行测试,该数据涉及人的智力水平和自行车的速度的关系。当然,数据是假的。
3.2、开发流程
收集数据:采用任意方法收集数据
准备数据:需要数值型数据,标称型数据应该映射成二值型数据
分析数据:绘出数据的二维可视化显示结果,以字典方式生成树
训练算法:模型树的构建
测试算法:使用测试数据上的R^2值来分析模型的效果
使用算法:使用训练出的树做预测,预测结果还可以用来做很多事情
收集数据: 采用任意方法收集数据
准备数据:需要数值型数据,标称型数据应该映射成二值型数据
数据存储格式:
数据集为bikeSpeedVsIq_test.txt和bikeSpeedVsIq_train.txt
数据集下载地址:数据集下载
3.000000 46.852122
23.000000 178.676107
0.000000 86.154024
6.000000 68.707614
15.000000 139.737693
分析数据:绘出数据的二维可视化显示结果,以字典方式生成树
训练算法:模型树的构建
用树回归进行预测的代码
# 回归树测试案例
# 为了和 modelTreeEval() 保持一致,保留两个输入参数
def regTreeEval(model, inDat):
"""
Desc:
对 回归树 进行预测
Args:
model -- 指定模型,可选值为 回归树模型 或者 模型树模型,这里为回归树
inDat -- 输入的测试数据
Returns:
float(model) -- 将输入的模型数据转换为 浮点数 返回
"""
return float(model)
# 模型树测试案例
# 对输入数据进行格式化处理,在原数据矩阵上增加第0列,元素的值都是1,
# 也就是增加偏移值,和我们之前的简单线性回归是一个套路,增加一个偏移量
def modelTreeEval(model, inDat):
"""
Desc:
对 模型树 进行预测
Args:
model -- 输入模型,可选值为 回归树模型 或者 模型树模型,这里为模型树模型
inDat -- 输入的测试数据
Returns:
float(X * model) -- 将测试数据乘以 回归系数 得到一个预测值 ,转化为 浮点数 返回
"""
n = shape(inDat)[1]
X = mat(ones((1, n+1)))
X[:, 1: n+1] = inDat
# print X, model
return float(X * model)
# 计算预测的结果
# 在给定树结构的情况下,对于单个数据点,该函数会给出一个预测值。
# modelEval是对叶节点进行预测的函数引用,指定树的类型,以便在叶节点上调用合适的模型。
# 此函数自顶向下遍历整棵树,直到命中叶节点为止,一旦到达叶节点,它就会在输入数据上
# 调用modelEval()函数,该函数的默认值为regTreeEval()
def treeForeCast(tree, inData, modelEval=regTreeEval):
"""
Desc:
对特定模型的树进行预测,可以是 回归树 也可以是 模型树
Args:
tree -- 已经训练好的树的模型
inData -- 输入的测试数据
modelEval -- 预测的树的模型类型,可选值为 regTreeEval(回归树) 或 modelTreeEval(模型树),默认为回归树
Returns:
返回预测值
"""
if not isTree(tree):
return modelEval(tree, inData)
if inData[tree['spInd']] <= tree['spVal']:
if isTree(tree['left']):
return treeForeCast(tree['left'], inData, modelEval)
else:
return modelEval(tree['left'], inData)
else:
if isTree(tree['right']):
return treeForeCast(tree['right'], inData, modelEval)
else:
return modelEval(tree['right'], inData)
# 预测结果
def createForeCast(tree, testData, modelEval=regTreeEval):
"""
Desc:
调用 treeForeCast ,对特定模型的树进行预测,可以是 回归树 也可以是 模型树
Args:
tree -- 已经训练好的树的模型
inData -- 输入的测试数据
modelEval -- 预测的树的模型类型,可选值为 regTreeEval(回归树) 或 modelTreeEval(模型树),默认为回归树
Returns:
返回预测值矩阵
"""
m = len(testData)
yHat = mat(zeros((m, 1)))
# print yHat
for i in range(m):
yHat[i, 0] = treeForeCast(tree, mat(testData[i]), modelEval)
# print "yHat==>", yHat[i, 0]
return yHat
测试算法:使用测试数据上的R^2值来分析模型的效果
R^2 判定系数就是拟合优度判定系数,它体现了回归模型中自变量的变异在因变量的变异中所占的比例。如 R^2=0.99999 表示在因变量 y 的变异中有 99.999% 是由于变量 x 引起。当 R^2=1 时表示,所有观测点都落在拟合的直线或曲线上;当 R^2=0 时,表示自变量与因变量不存在直线或曲线关系。
所以我们看出, R^2 的值越接近 1.0 越好。
使用算法:使用训练出的树做预测,预测结果还可以用来做很多事情
具体我们可以参照这个完整代码进行编写查看:https://github.com/aimi-cn/AILearners/tree/master/src/py2.x/ml/jqxxsz/9.RegTrees/demo.py
AIMI-CN AI学习交流群【1015286623】 获取更多AI资料
扫码加群:
分享技术,乐享生活:我们的公众号计算机视觉这件小事每周推送“AI”系列资讯类文章,欢迎您的关注!