贪心算法求单源最短路径（迪杰斯特拉算法）

目录

1.单源最短路径问题描述

2.Dijkstra算法思想

3.具体案例分析

4.具体代码实现

---

1.单源最短路径问题描述

①给定带权有向图G =(V,E)。其中V是图中所有顶点的集合。E是图中所有边的集合，每条边的权是非负实数。

②给定V中的一个顶点，称为源。

③计算从源到所有其它各顶点的最短路长度。

而Dijkstra算法正是最具代表性的解单源最短路径问题的贪心算法。

2.Dijkstra算法思想

①设置顶点集合U，U表示已选择的节点，所以初始化的U中仅包含源结点。

②设置一张表，表中记录的是U外V内（V含义参见上面）的结点到U中任意结点的距离的最小值。

③不断地作贪心选择，选择不在U集合中的结点来加入这个集合。

④每当一个结点加入这个集合后，更新其他未加入的结点到U中任意一点的距离的最小值。

⑤当所有结点都加入到U中后即算法完成。

Question：加入集合=确定路径?能确保是最短路径吗？

Answer：

初始化时集合内只有源节点。

考虑加入集合的第一个节点：

当要选择第一个加入集合的结点时，我们选择与源节点有边且边权值最小的节点。

为什么呢？因为此节点到源节点的距离走这条边肯定是最短的。

举个例子：

假设源结点v，与它与边关系的只有结点a、b。且v→a=10，v→b=20。

如果v→a这条边被你放弃的话，再想要从v走到a就必须经过v→b→其他节点→a。代价至少是20+，必大于10。

所以此时将a加入U是最好的，源节点到a的距离肯定是最短的。

考虑后来的其他节点：

从第一个节点的加入，说明了集合内的点都是已经确定由源节点走到它的最短距离了。

所以可以放心地把集合内的点看成一个整体。

那么计算集合外的节点到集合的最近距离，选择最小的加入到集合中，直到所有结点都加入到集合中。

3.具体案例分析

4.具体代码实现

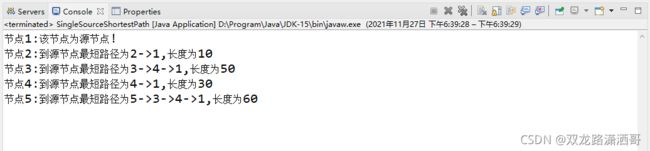
public class SingleSourceShortestPath {

	public static void main(String[] args) {

		//节点数量
		int num = 5;
		//源节点
		int sourcev = 1;
		
		/*
		 * 5个节点，但设邻接矩阵为c[6][6]
		 * 这样c[1][2]就表示第一个节点到第二个节点的距离，较好理解
		 * 故：
		 * 因没有第0个节点，邻接矩阵第一行、第一列作废，设为-1
		 * 因节点自身到自身无意义，邻接矩阵左至右对角线作废，设为-1
		 */
		int[][] c = {{-1,-1,-1,-1,-1,-1},
					 {-1,-1,10,-1,30,100},
					 {-1,10,-1,50,-1,-1},
					 {-1,-1,50,-1,20,10},
					 {-1,30,-1,20,-1,60},
					 {-1,100,-1,10,60,-1}};
		
		//结果
		int[][] result = dijkstra(num,c,sourcev);
		for (int i = 1; i <= num; i++) {
			System.out.print("节点" + i + ":");
			if(i == sourcev) {
				System.out.println("该节点为源节点!");
			}else {
				System.out.print("到源节点最短路径为" + i + "->");
				int index = result[0][i];
				while(index != sourcev) {
					System.out.print(index + "->");
					index = result[0][index];
				}
				System.out.println(sourcev + ",长度为" + result[1][i]);
			}
		}
	}

	/**
	 * 
	 * @param num 节点的数量
	 * @param c 邻接矩阵
	 * @param sourcev 源节点
	 * @return 一个数组，数组的第0行表示节点的前驱节点，数组的第1行表示源到节点的距离。
	 */
	private static int[][] dijkstra(int num, int[][] c, int sourcev) {
		
		int[][] prevANDdist = new int[2][num+1];
		boolean[] isChosen = new boolean[num+1];
		
		//初始化
		for (int i = 1; i < prevANDdist[0].length; i++) {
			if(i == sourcev) {
				prevANDdist[0][i] = -1;
				prevANDdist[1][i] = Integer.MAX_VALUE;
				isChosen[sourcev] = true;
			}else {
				if(c[i][sourcev] != -1) {
					prevANDdist[0][i] = sourcev;
					prevANDdist[1][i] = c[i][sourcev];
					isChosen[i] = false;
				}else {
					prevANDdist[0][i] = -1;
					prevANDdist[1][i] = Integer.MAX_VALUE;
					isChosen[i] = false;
				}
			}
		}
		
		//因为要依次加入除去源节点外的num-1个节点，所以要循环num-1次。
		for (int i = 1; i <= num-1; i++) {
			int tempv = 0;
			int tempdist = Integer.MAX_VALUE;
			//选取下一个节点
			for (int j = 1; j <= num; j++) {
				if(isChosen[j]==false && prevANDdist[1][j]

---

2021/11/27

2022/05/28修改部分表达。