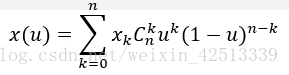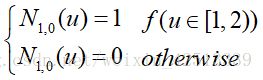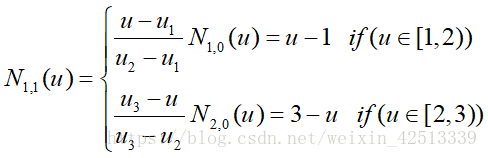B样条曲线

学习B样条曲线需要先学习贝塞尔曲线，若未了解，看我一篇上博客https://blog.csdn.net/weixin_42513339/article/details/83019610

贝塞尔函数不足

由于贝塞尔曲线存在以下不足：

        1 ）缺乏局部修改性，即改变某一控制点对整个曲线都有影响。

        2 ）n 较大时，特征多边形的边数较多，对曲线的控制减弱。

        3 ）幂次过高难于修改。（而在外形设计中，局部修改是随时要进行的）。

所以提出了B样条曲线，B样条曲线有以下优点：

  1 ）逼近特征多边形的精度更高。

  2 ）多边形的边数与基函数的次数无关。

  3 ）具有局部修改性。

首先，贝塞尔公式为：

其中，  为伯恩斯坦基函数（BEZ）

 

所以公式可以写成

 

B样条曲线

B样条曲线，用B样条基函数代替伯恩斯坦基函数如下所示：

这里的你只是一个比例系数，但是这里把你从0到1分成很多段。如果节点等间距（即  ui +1 -  ui  是一个常数，对0 <=  i  <=  m  - 1），节点向量或节点序列称为均匀的;否则它是非均匀的。

节点可认为是分隔点，将区间[ u0，um]细分为节点区间。所有B样条基函数被假设定义域在[ u0，um ]上。uo  = 0和um  = 1，所以定义域是闭区间[0,1]。

相关定义

在图形学书里，也写明了若此时线段的顶点个数为m + n + 1（m为最大段号，n为阶次）

B样条曲线主要也是为了平滑曲线，而且这里的阶次，换个说法就是目前这个点能够影响它附近多少个点。

 

多重节点与简单节点

如果一个节点ui出现k次（即，ui = ui + 1 = ... = ui + k-1），其中k> 1，ui是一个重复度（multiplicity）为k 的多重节点，写ui（k否则），如果用户界面只出现一次，它是一个简单节点。

 

B样条基函数

区间我的ķ次B样条基函数，写为镍，K（U），递归定义如下：

K = 0时的Ni，k（u）
    如果次数为零（即k = 0），这时基函数都是阶梯函数，如果你是在第i个节点区间[ui，ui + 1）上，那么基函数的Ni，0（U）= 1。
 

例：
    有四个节点U = {0,1,2,3}，节点区间0,1,2分别对应[0,1），[1,2），[2,3]。（这里你的范围也只是一个比例关系）

  

画出图如下所示：

 

若K = 1时的的Ni，K（U）

下图中，黑色和红色线分别是N0,1（u）和N1,1（u）。

 

PS：

 为了理解 阶数k 大于0时，计算Ni，k（u）的方法，我们使用三角计算格式。所有节点区间列在左边（第一）列，所有零次基函数在第二列。见下图。

从这一张图里，我们可以很清楚的看到，如果想计算某个基函数，那么就必须要知道哪些零次基函数，然后需要哪两个计算，都可以从图里看出来。

比如：

我们继续计算K = 2时的镍，K（U），如下：

其中，当你在[0,1）上时，这种情况，只有N0,1（u）对N0,2（u）的值有贡献。因此，N0,1（u）是你，得到

你在[1,2]上： 

这种情况，N0,1（u）和N1,1（u）都对N0,2（u）有贡献。在[1,2]上N0,1（u）= 2 - u和N1,1（ u）= u - 1，得到： 

你在[2,3]上： 

这种情况，只有N1,1（u）对N0,2（u）有贡献。在[2,3]上N1,1（u）= 3 - u，得到：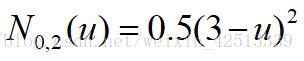

可以最后得到N0,2（u）函数图形 

 

基函数的非零定义域的确定

实际上也是主要通过图来看如下图，我们可以得知：如果我们要计算N1,3（U），那么它的有效定义域是u1到u5通过下图可以直接看出。

说的更加理论一点就是：

基函数Ni，p（u）在[ui，ui + k + 1）上非零。或，相等地，Ni，k（u）在k + 1个节点区间[ui，ui + 1]，[ui + 1，ui + 2），...，[ui + k，ui + k + 1）上非零。

在这里，我们可以观察出重要的一点，为什么B样条曲线的顶点数是m + n + 1，因为跟它的定义域是有关的。

 

非零定义域对应的基函数

与上面正好相反，我们可以通过基函数的阶数，来确定他的定义域。

同样，一个定义域，我们也可以看出（如下图）：

任何一个节点区间[ui，ui + 1]，最多有k + 1个k次基函数非零，即：Ni-k，k（u），Ni-k + 1，k（u），Ni-k + 2，k（u），...，Ni-1，k（u）和Ni，k（u）。

 

系数的意义

第一项，Ni，k-1（u），在[ui，ui + k）上非零。如果u是在该区间，那么你 - ui是u到该区间左端的距离，区间长度为ui + k - ui，（u - ui）/（ui + k - ui）是你在上述区间的归一化位置。

第二项，Ni + 1，k-1（u），在[ui + 1，ui + k + 1）上非零。如果u在该区间，那么ui + k + 1 - u是u到该区间右端的距离，ui + k + 1 - ui + 1是区间长度，（ui + k + 1 - u）/（ui + k + 1 - ui + 1）是u在上述区间的归一化位置。