数学建模学习(1)———— 逻辑回归的使用和案例(2022.7.18)
许多数学建模的使用基本都是一元线性回归,和多元线性回归开始,但由于经常看关于这两个东西,实在不想从这开始整理笔记,等后面印象不深后在整理过。
文章目录
目录
文章目录
一、逻辑回归介绍
二、逻辑回归代码实现
2.1 构造数据
2.2 导入库拟合数据,打印预测。
2.3 打印概率
2.4 计算系数和截距
三、逻辑回归案例 ——股票客户流失案例
3.1 数据预处理
3.2. 模型的搭建与使用
一、逻辑回归介绍
逻辑回归是一种分类模型,但为什么会含有回归二字了,是因为算法原理同样涉及到回归方程,方程如下:
![]()
上面个方程是用来预测连续变量的,取值范围为R
逻辑回归,是用来预测物体是a类还是b类,但本质其实是预测该物体属于a或b的概率,而概率的取值范围为(0,1),所以不能直接用线性回归方程来预测概率,那么如何把一个取值范围是R的回归方程变为取值范围为(0,1)的内容了?
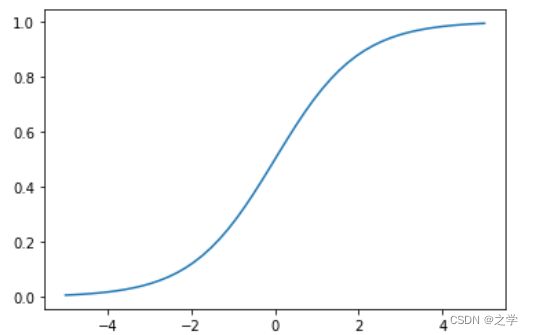
我们就需要,使用Sigmoid函数![]() ,python画出函数图像实例如下:
,python画出函数图像实例如下:
# sigmoid
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-5,5)
y = 1/(1+np.exp(-x))
plt.plot(x,y)
plt.show()out:
逻辑回归模型的本质就是预测各个分类的概率,有了概率时候就可以进行分类,列如在预测顾客是否会违约的模型中,如果预测违约的概率P为70%则不违约的概率为30%,就会认为,顾客属于违约这一类。在实际模型的搭建中使用极大似然估计法,找到合适的系数k,可截距k0,使预测结果较为准确。
二、逻辑回归代码实现
2.1 构造数据
| |
||
|---|---|---|
| 1 | 5 | 0 |
| 3 | 2 | 1 |
| 8 | 5 | 0 |
| 4 | 6 | 1 |
| 4 | 1 | 0 |
2.2 导入库拟合数据,打印预测。
x = [[1,5],[3,2],[8,5],[4,6],[4,1]]
Y = [0,1,0,1,0]
from sklearn.linear_model import LogisticRegression
model = LogisticRegression()
model.fit(x,Y)
print(model.predict([[1,9]]))out:
[1]
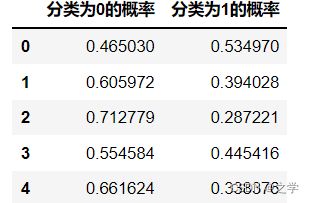
2.3 打印概率
import pandas as pd
y_ks = model.predict_proba(x)
a = pd.DataFrame(y_ks,columns = ['分类为0的概率','分类为1的概率'])
print(a)out:
2.4 计算系数和截距
print(model.coef_)#计算系数k1,k2
print(model.intercept_)#计算截距k0out:
[[-0.14986103 0.09026635]] [-0.16136302]
三、逻辑回归案例 ——股票客户流失案例
3.1 数据预处理
这个数据是已经处理好了的,但在建模过程中,一般都要自己处理数据。这里直接导入数据。分离x和y。
import pandas as pd
df = pd.read_excel('股票客户流失.xlsx')
print(df.head())这里先打印前5行看一看
划分特征量,和目标变量:
X = df.drop(columns = '是否流失')
y = df['是否流失']3.2. 模型的搭建与使用
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
# 划分测试集和训练集
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2)
# 模型搭建
model = LogisticRegression()
model.fit(X_train,y_train)
# 预测数据结果,这里打印100行看看
y_pred = model.predict(X_test)[0:100]
print(y_pred)#0表示流失,1表示不流失
print(model.score(X_test,y_test))#打印准确度out:
[0 0 0 0 1 1 0 0 0 0 1 0 0 0 1 0 0 1 0 0 0 0 0 1 0 0 1 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 1 0 0 0 0] 0.7709377236936292
可以看到,模型最后的准确度是很高的,证明模型可以用。
需要数据的小伙伴,关注即可私聊拿数据。