(这道题我完全是看这别人的博客打出来的orz...)
下面就说说我对这道题的感悟。。。
add操作
splay的规则使得平衡树在旋转过程中可以保证其正确性(节点左儿子小于节点,节点右儿子大于节点),因为splay也是二叉树,我们也可以在上面同时用线段树的做法。
但是有一点不同的是splay其实是在不断旋转的,同时符合平衡树性质也有很多不同的节点组合方法,在旋转过程中一个节点的左右子节点会发生变化
比如:
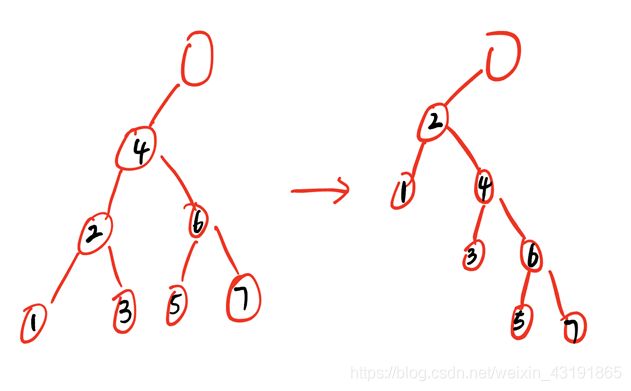
(2号节点的左右儿子在不断发生变化,但是之前我们使用线段树的时候是静态地维护树上的信息)
在线段树区间更新的时候,我们需要使用延迟标记,而对于不断变化的平衡树,则需要:
1.在旋转的时候需要及时的将需要旋转的节点的延迟标记更新给其子节点
2.需要将节点旋转到合适的地方使得我们能正确的使用延迟标记标记一段区间
因此假如要为l~r区间内所有项都加上一个数的话,首先我们需要将l~r区间放到一起,因此将l-1旋转到根,r+1旋转到根的右儿子,此时l~r就是根的右儿子的左儿子了。
然后打上lazy标记即可
翻转操作
假如要将[l,r]区间翻转的话,和add一样首先要找到l,r区间,因此将l-1区间splay到根节点,r+1区间splay到根节点的右儿子,此时l,r区间就得到了
那么翻转操作实际上如何在平衡树中体现呢,事实上平衡树的中序遍历的结果得到的就是原区间。
因此问题可以转化为对一棵二叉树我需要中序遍历得到其序列的翻转,那么二叉树要怎么调整呢?
看看中序遍历的代码
二叉树的中序遍历(递归)
void output(int x){
output(左儿子)
输出x
output(右儿子)
}
假如需要逆序得到二叉树,那么可以这么改
二叉树的中序遍历(递归)
得到逆序
void output(int x){
output(右儿子)
输出x
output(左儿子)
}
对比上面两个代码得知,我只需要将区间中每一个节点的左右儿子互换,那么我就可以将一个区间翻转了
所以对于上面得到的代表l~r区间的子树,将这棵子树里面每一个节点的左右儿子都互换即可得到逆序区间
同时,对于一个区间假如连续翻转两次的话,相当于没有翻转,这点暗示我们翻转也可以采用延迟标记的方法。
轮换操作:
比如说要轮换k次,那么只是将区间最右边k个数剪切到区间最左边即可
因此首先找到需要剪切的区间(通过splay将区间找到),然后剪下来(区间的父节点和区间之间的连线断开,然后保存剪下来的区间的根节点序号)
接着拼接到区间最左边,比如区间最左边的编号是l,那么我们需要找到 l-1 和 l的编号,然后分别splay(l-1,0) , splay(l,l-1),此时
因为l和l-1是相连的,因此ch[l][0] = 0 ,将剪下来的区间粘贴到 ch[l][0] 处即可(建立双方连线)
(这个具体可以看一下代码)
插入操作 :
同样和上面轮换操作的拼接类似,要插入一个点首先要找到那个点前后的两个节点,比如要在 x和y 之间插入一个点,那么就将x节点旋转到根,将y节点旋转到其父节点为x节点,即splay(x,0) , splay(y,x) , 此时因为本来x,y是相连的,因此ch[y][0] = 0 ,而我们只需要在ch[y][0]这个地方插入一个点即可(建立双方连线)
删除操作:
比如需要删除x节点,那么则需要将x-1旋转到根,将x+1旋转到其父亲节点为x-1即可,然后将ch[x+1][0]就是x节点,此时断开连接即可。
MIN操作;
同理,要查看[l,r]区间的min操作,首先要找到l,r区间,做法就是splay(l-1,0) , splay(r+1,l-1) ,然后因为对于节点我们有维护节点及其子节点的min值,此时直接输出ch[r+1][0]的min属性即可
最后一点感悟:
使用splay的时候为其初始化两个节点往往是非常好用的。
比如插入操作,需要在x后面插入一个值为val的点的时候,正常来说应该先检查一下x后面是否还有点,然后再决定是否splay,但是假如开始的时候就为序列两端初始化上-INF和INF,这个时候就不需要检查x后面是否还有点了,因为这是必然的。
#include
#include
#include
#include
#include
#include
#include
#include

