Attention及其pytorch代码实现

基于RNN的Seq2Seq的基本假设：原始序列的最后一个隐含状态（一个向量）包含了该序列的全部信息。（这显然是不合理的）

Seg2Seg问题：记忆长序列能力不足

解决：当要生成一个目标语言单词的时候，不光考虑前一个时刻的状态和已经生成的单词，还要考虑当前要生成的单词和源句子中的哪些单词更加相关，即更关注源句子中的哪些词，这种做法就叫做注意力机制（Attention）

Attention

Luong等人在2015年发布的Effective Approaches to Attention-based Neural Machine Translation论文中，提出了attention技术，通过attention技术，seg2seg模型极大地提高了机器翻译的质量。

归其原因是：attention机制使得seg2seg模型可以有区分度、有重点地关注输入序列。

实例：

1. 假设模型已经生成单词“我”之后，要生成下一个单词；
2. 显然和源语言中“love”关系最大，因此将源语言句子中的“love”对应的状态乘以一个比较大的权重，如0.6，而其余词的权重则较小；
3. 最终将源语言句子中每个单词对应的状态加权求和，并用作新状态更新一个额外输出。

结合Attention机制的Seg2Seg模型

• 结合attention， seg2seg模型decoder每次更新状态的时候都会再看一遍encoder的所有状态（decoder会知道去关注哪里）

• 在Encoder结束工作之后，Attention和Decoder同时开始工作

• attention可以简单的理解为：一种有效的加权求和技术，关键点在于如何获得权重。

• 计算权重：${\alpha }_i=aligh(h_i,s_0)$
  （相当于计算$h_i$和$s_0的相关性$）
  （$h_i为Encoder的隐藏层状态，s_0为Encoder的最后一个隐藏层状态$）
  （权重为0-1之间的数，加起来等于1）
• 计算方法：

1. Linear maps(线性变换)：
   $$k_i=W_K\cdot h_i，fori=1tom$$$$q_0=W_Q\cdot s_0$$
2. Inner product（计算内积）：
   $$\widetilde{{\alpha }_i}={\mathbf{k}}_i^{\mathrm{T}}{q}_0$$
3. Normalization:
   $$[{\alpha }_1,\cdot \cdot \cdot ，{\alpha }_m]=softmax([\widetilde{{\alpha }_1},\cdot \cdot \cdot ,\widetilde{{\alpha }_m}])$$

计算权重还有另一种方法，本文的代码中用到了，但现在更为主流的是第一种方法

• 获得权重之后就是求取Context Vector:

$$c_0={\alpha }_1{h}_1+\cdot \cdot \cdot +{\alpha }_m{h}_m$$

• 更新Decoder状态向量($s_0=h_m$)

1. SimpleRNN
   $$s_1=tanh(A^{\prime }\cdot \left[\begin{array}{c}{X}_1^{\prime }\\ s_0\end{array}\right]+b)$$
2. SimpleRNN+Attention
   $$s_1=tanh(A^{\prime }\cdot \left[\begin{array}{c}{X}_1^{\prime }\\ s_0\\ c_0\end{array}\right]+b)$$

• 缺点：计算量非常大
• attention时间复杂度很高$mt$（encoder和decoder序列长度的乘积）

GRU

由于后面的代码用到了GRU，这里简单介绍一下。

GRU（Gate Recurrent Unit）是RNN的一种。和LSTM一样，也是为了解决长期记忆和反向传播中的梯度等问题而提出的。

GRU输入输出的结构和普通的RNN相似，其中内部思想与LSTM相似。

与LSTM相比，GRU内部少了一个Gate，参数相对更少，训练速度更快，但是也能达到和LSTM相当的功能。

GRU的输入输出

• 和RNN一样，没什么好说的

GRU的内部结构

1. 通过前一时刻状态$h_{t-1}$和当前输入$x_t$来获取两个门控状态
   $$重置门控：r=\sigma (W^r\cdot \left[\begin{array}{c}{x}_t\\ h_{t-1}\end{array}\right])$$$$更新门控：z=\sigma (W^z\cdot \left[\begin{array}{c}{x}_t\\ h_{t-1}\end{array}\right])$$

2. 得到门控信息后，首先使用重置门控来得到重置之后的数据$$h_{t-1}^{{}^{\prime }}=h_{t-1}\cdot r$$再将$h_{t-1}^{{}^{\prime }}$与输入$x_t$进行拼接，再通过一个tanh函数来将数据缩放到-1~1之间$$h^{\prime }=tanh(W\left[\begin{array}{c}{x}_t\\ h_{t-1}^{{}^{\prime }}\end{array}\right])$$这里的$h^{\prime }$主要是包含了当前输入$x_t$，有针对性的添加了上一时刻的隐藏层状态，类似与LSTM的forget gate。

3. 更新记忆阶段
   在这个阶段，我们同时进行了遗忘和记忆两个步骤。
   先使用了之前得到的更新门控$$h_t=(1-z)\cdot h_{t-1}+z\cdot h^{\prime }$$
   GRU的关键点就在于此：使用更新门控$z$就可以同时进行遗忘和选择记忆

代码实现

任务：机器翻译
源语言：德语
目标语言：英语

• 导入包

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F

from torchtext.legacy import data,datasets

import spacy
import numpy as np

import random
import math

import de_core_news_sm

数据预处理

• 设置种子

SEED = 1234

random.seed(SEED)
np.random.seed(SEED)
torch.manual_seed(SEED)
torch.cuda.manual_seed(SEED)
torch.backends.cudnn.deterministic = True

• 接下来，我们将加载spaCy模块，并为源语言和目标语言定义标记器。（这里比较麻烦，建议从spacy的github直接下载，然后安装）

spacy_de = spacy.load('de_core_news_sm')
spacy_en = spacy.load('en_core_web_sm')

• 构建分词器

def tokenize_de(text):
    # Tokenizes German text from a string into a list of strings
    return [tok.text for tok in spacy_de.tokenizer(text)]

def tokenize_en(text):
    # Tokenizes English text from a string into a list of strings
    return [tok.text for tok in spacy_en.tokenizer(text)]

• 接下来，我们将设置决定如何处理数据的字段。我们附加了序列标记的开始和结束，并对所有文本进行小写。

SRC = data.Field(tokenize = tokenize_de, 
            init_token = '', 
            eos_token = '', 
            lower = True)

TRG = data.Field(tokenize = tokenize_en, 
            init_token = '', 
            eos_token = '', 
            lower = True)

---

• 我们加载训练集、验证集和测试集，生成dataset类。使用torchtext自带的Multi30k数据集，这是一个包含约30000个平行的英语、德语和法语句子的数据集，每个句子包含约12个单词。

train_data, valid_data, test_data = datasets.Multi30k.splits(exts = ('.de', '.en'),
															fields = (SRC, TRG))

• 可以查看以下加载完的数据集

print(f"Number of training examples: {len(train_data.examples)}")
print(f"Number of validation examples: {len(valid_data.examples)}")
print(f"Number of testing examples: {len(test_data.examples)}")

Number of training examples: 29000
Number of validation examples: 1014
Number of testing examples: 1000

• 查看数据实例

vars(train_data.examples[0])

{'src': ['zwei',
  'junge',
  'weiße',
  'männer',
  'sind',
  'im',
  'freien',
  'in',
  'der',
  'nähe',
  'vieler',
  'büsche',
  '.'],
 'trg': ['two',
  'young',
  ',',
  'white',
  'males',
  'are',
  'outside',
  'near',
  'many',
  'bushes',
  '.']}

---

• 构建词汇表，将出现次数少于2次的任何标记转换为标记。

SRC.build_vocab(train_data, min_freq = 2)
TRG.build_vocab(train_data, min_freq = 2)

• 查看一下生成的词表大小

print(f"Unique tokens in source (de) vocabulary: {len(SRC.vocab)}")
print(f"Unique tokens in target (en) vocabulary: {len(TRG.vocab)}")

Unique tokens in source (de) vocabulary: 7855
Unique tokens in target (en) vocabulary: 5893

• 查看词汇表中最常见的单词及其他们在数据集中出现的次数。

SRC.vocab.freqs.most_common(20)

[('.', 28809),
 ('ein', 18851),
 ('einem', 13711),
 ('in', 11895),
 ('eine', 9909),
 (',', 8938),
 ('und', 8925),
 ('mit', 8843),
 ('auf', 8745),
 ('mann', 7805),
 ('einer', 6765),
 ('der', 4990),
 ('frau', 4186),
 ('die', 3949),
 ('zwei', 3873),
 ('einen', 3479),
 ('im', 3107),
 ('an', 3062),
 ('von', 2363),
 ('sich', 2273)]

• 也可以使用 stoi (string to int) or itos (int to string) 方法，以下输出TRG-vocab的前10个词汇。

print(TRG.vocab.itos[:10])

# ['', '', '', '', 'a', '.', 'in', 'the', 'on', 'man']

---

• 设置GPU，构建迭代器

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

BATCH_SIZE = 64

train_iterator, valid_iterator, test_iterator = data.BucketIterator.splits(
    (train_data, valid_data, test_data), 
    batch_size = BATCH_SIZE, 
    device = device)

• 查看一下生成的batch

batch = next(iter(train_iterator))
print(batch)

[torchtext.legacy.data.batch.Batch of size 64 from MULTI30K]
	[.src]:[torch.cuda.LongTensor of size 25x64 (GPU 0)]
	[.trg]:[torch.cuda.LongTensor of size 28x64 (GPU 0)]

搭建模型

Encoder

Encoder用的是单层双向GRU

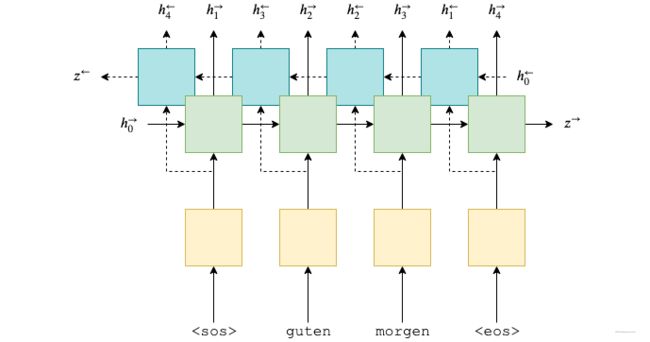
• 双向GRU的隐藏层状态输出由两个向量拼接而成

  例如：$$h_1=[h_1;h_T];h_2=[h_2;h_{T-1}];..........$$
  $$output=\{h_1,h_2,......h_T\}$$

• 假设这是个m层的GRU$$hidden=\{[h_T^1;h_1^1],[h_T^2;h_1^2],......,[h_T^m;h_1^m]\}$$

• 我们需要的是hidden的最后一层输出（包括正向和反向），因此我们可以通过hidden[-2,:,:]和hidden[-1,:,:]取出最后一层的hidden state，将他们拼接起来记作$s_0$。

• $s_0$的维度变换(我们需要将$s_0$维度变换到匹配decoder的初始隐藏状态)

  1. enc_hidden:[n_layersnum_directions, batch_size, hid_dim2]
  2. 由于是双向的，做concat：[batch_size, enc_hid_dim*x]
  3. 经过一个全连接层：[batch_size,dec_hid_dim]
  4. 剩下还需要进行unsqueeze 和 repeat，这将在下一步完成。

class Encoder(nn.Module):
    def __init__(self, input_dim, emb_dim, enc_hid_dim, dec_hid_dim, dropout):
        super().__init__()
        self.embedding = nn.Embedding(input_dim, emb_dim)
        self.rnn = nn.GRU(emb_dim, enc_hid_dim, bidirectional = True)
        self.fc = nn.Linear(enc_hid_dim * 2, dec_hid_dim)
        self.dropout = nn.Dropout(dropout)
        
    def forward(self, src): 
        '''
        src = [src_len, batch_size]
        '''
        src = src.transpose(0, 1) # src = [batch_size, src_len]
        embedded = self.dropout(self.embedding(src)).transpose(0, 1) # embedded = [src_len, batch_size, emb_dim]
        
        # enc_output = [src_len, batch_size, hid_dim * num_directions]
        # enc_hidden = [n_layers * num_directions, batch_size, hid_dim]
        enc_output, enc_hidden = self.rnn(embedded) # if h_0 is not give, it will be set 0 acquiescently

        # enc_hidden is stacked [forward_1, backward_1, forward_2, backward_2, ...]
        # enc_output are always from the last layer
        
        # enc_hidden [-2, :, : ] is the last of the forwards RNN 
        # enc_hidden [-1, :, : ] is the last of the backwards RNN
        
        # initial decoder hidden is final hidden state of the forwards and backwards 
        # encoder RNNs fed through a linear layer
        # s = [batch_size, dec_hid_dim]
        s = torch.tanh(self.fc(torch.cat((enc_hidden[-2,:,:], enc_hidden[-1,:,:]), dim = 1)))
        # s就是隐藏层输出，之后作为decoder的初始隐藏状态
        # 由于维度不匹配，经历了一个全连接网络改变维度，以适应decoder的初始隐藏层维度。
        # 之后还需要unsqueeze(0)
        
        return enc_output, s

Attention

$$E_t=tanh[attn(s_{t-1},H)]$$$${\tilde{\alpha }}_t=v\cdot E_t$$$${\alpha }_t=softmax({\tilde{\alpha }}_t)$$

1. $s_{t-1}是指encoder的隐藏层输出$
2. $H指的是Encoder中的变量enc\_ouput$
3. attn()其实就是一个简单的全连接神经网络。

维度变换：

1. 首先将encoder传过来的s变换成[batch_size, src_len, dec_hid_dim]
2. enc_output进行transpose–>[batch_sizr, src_len, enc_hid_dim*2]好让他们可以concat
3. 运算第一个公式得到energy [batch_size,src_len, dec_hid_dim]
4. 第二个公式，线性变换 [batch_size,src_len,1] 然后squeeze（2）去掉最后一个维度
5. 最后就是softmax，不改变维度。

返回的就是权重值

class Attention(nn.Module):
    def __init__(self, enc_hid_dim, dec_hid_dim):
        super().__init__()
        self.attn = nn.Linear((enc_hid_dim * 2) + dec_hid_dim, dec_hid_dim, bias=False)
        self.v = nn.Linear(dec_hid_dim, 1, bias = False)
        
    def forward(self, s, enc_output):
        
        # s = [batch_size, dec_hid_dim]
        # enc_output = [src_len, batch_size, enc_hid_dim * 2]
        
        batch_size = enc_output.shape[1]
        src_len = enc_output.shape[0]
        
        # repeat decoder hidden state src_len times
        # s = [batch_size, src_len, dec_hid_dim]
        # enc_output = [batch_size, src_len, enc_hid_dim * 2]
        s = s.unsqueeze(1).repeat(1, src_len, 1)
        enc_output = enc_output.transpose(0, 1)
        
        # energy = [batch_size, src_len, dec_hid_dim]
        energy = torch.tanh(self.attn(torch.cat((s, enc_output), dim = 2)))
        
        # attention = [batch_size, src_len]
        attention = self.v(energy).squeeze(2)
        
        return F.softmax(attention, dim=1)

Decoder

• Decoder用的是单向单层GRU
  

实际也就三个公式：

1. 利用attention部分求得的权重计算context vector$$c={\alpha }_{t}H$$
2. 更新decoder状态向量$$s_t=GRU(emb(y_t),c,s_{t-1})$$
3. $$\widehat{y_t}=f(emb(y_t),c,s_t)$$

• $H指的是Encoder中的变量enc\_ouput$
• $emb(y_t)指的是将dec\_input经过WordEmbedding之后得到的结果$
• $f()函数实际上就是为了转换维度$

• torch.bmm 维度为3的两个tensor矩阵相乘
  

维度变换

1. decoder中最开始先调用一次attention,得到权重${\alpha }_t$,它的维度是[batch_size, src_len]

class Decoder(nn.Module):
    def __init__(self, output_dim, emb_dim, enc_hid_dim, dec_hid_dim, dropout, attention):
        super().__init__()
        self.output_dim = output_dim
        self.attention = attention
        self.embedding = nn.Embedding(output_dim, emb_dim)
        self.rnn = nn.GRU((enc_hid_dim * 2) + emb_dim, dec_hid_dim)
        self.fc_out = nn.Linear((enc_hid_dim * 2) + dec_hid_dim + emb_dim, output_dim)
        self.dropout = nn.Dropout(dropout)
        
    def forward(self, dec_input, s, enc_output):
             
        # dec_input = [batch_size]
        # s = [batch_size, dec_hid_dim]
        # enc_output = [src_len, batch_size, enc_hid_dim * 2]
        
        dec_input = dec_input.unsqueeze(1) # dec_input = [batch_size, 1]
        
        embedded = self.dropout(self.embedding(dec_input)).transpose(0, 1) # embedded = [1, batch_size, emb_dim]
        
        # a = [batch_size, 1, src_len]  
        a = self.attention(s, enc_output).unsqueeze(1)
        
        # enc_output = [batch_size, src_len, enc_hid_dim * 2]
        enc_output = enc_output.transpose(0, 1)

        # c = [1, batch_size, enc_hid_dim * 2]
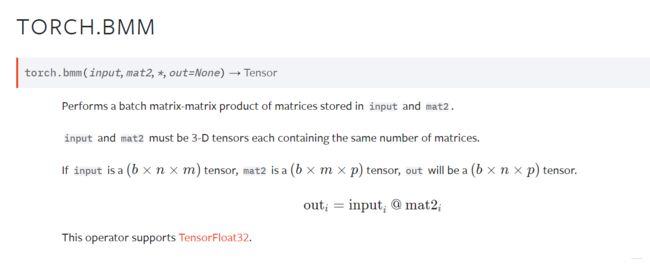
        c = torch.bmm(a, enc_output).transpose(0, 1)

        # rnn_input = [1, batch_size, (enc_hid_dim * 2) + emb_dim]
        rnn_input = torch.cat((embedded, c), dim = 2)
            
        # dec_output = [src_len(=1), batch_size, dec_hid_dim]
        # dec_hidden = [n_layers * num_directions, batch_size, dec_hid_dim]
        dec_output, dec_hidden = self.rnn(rnn_input, s.unsqueeze(0))
        
        # embedded = [batch_size, emb_dim]
        # dec_output = [batch_size, dec_hid_dim]
        # c = [batch_size, enc_hid_dim * 2]
        embedded = embedded.squeeze(0)
        dec_output = dec_output.squeeze(0)
        c = c.squeeze(0)
        
        # pred = [batch_size, output_dim]
        pred = self.fc_out(torch.cat((dec_output, c, embedded), dim = 1))
        
        return pred, dec_hidden.squeeze(0)

Seg2Seg（with attention）

class Seq2Seq(nn.Module):
    def __init__(self, encoder, decoder, device):
        super().__init__()
        self.encoder = encoder
        self.decoder = decoder
        self.device = device
        
    def forward(self, src, trg, teacher_forcing_ratio = 0.5):
        
        # src = [src_len, batch_size]
        # trg = [trg_len, batch_size]
        # teacher_forcing_ratio is probability to use teacher forcing
        
        batch_size = src.shape[1]
        trg_len = trg.shape[0]
        trg_vocab_size = self.decoder.output_dim
        
        # tensor to store decoder outputs
        outputs = torch.zeros(trg_len, batch_size, trg_vocab_size).to(self.device)
        
        # enc_output is all hidden states of the input sequence, back and forwards
        # s is the final forward and backward hidden states, passed through a linear layer
        enc_output, s = self.encoder(src)
                
        # first input to the decoder is the  tokens
        dec_input = trg[0,:]
        
        for t in range(1, trg_len):
            
            # insert dec_input token embedding, previous hidden state and all encoder hidden states
            # receive output tensor (predictions) and new hidden state
            dec_output, s = self.decoder(dec_input, s, enc_output)
            
            # place predictions in a tensor holding predictions for each token
            outputs[t] = dec_output
            
            # decide if we are going to use teacher forcing or not
            teacher_force = random.random() < teacher_forcing_ratio
            
            # get the highest predicted token from our predictions
            top1 = dec_output.argmax(1) 
            
            # if teacher forcing, use actual next token as next input
            # if not, use predicted token
            dec_input = trg[t] if teacher_force else top1

        return outputs

参考

• RNN模型与NLP应用(8/9)：Attention (注意力机制)
• Seq2Seq (Attention) 的 PyTorch 实现
• Datawhale（learning-nlp-with-transformers）
• 人人都能看懂的GRU
• Pytorch实现Seq2Seq模型：以机器翻译为例
• 卷积序列到序列模型的学习（Convolutional Sequence to Sequence Learning）