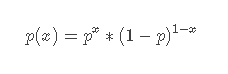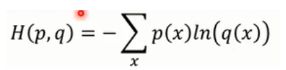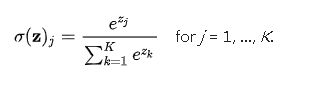逻辑回归模型(Logistic Regression)
逻辑回归符合伯努利分布。伯努利分布就是我们常见的0-1分布，即它的随机变量只取0或者1，各自的频率分别取1−p和p，当x=0或者x=1时，我们数学定义为：
所以在常规的逻辑回归模型中，只有两个类别，0或者1，适合二分类问题。
模型函数
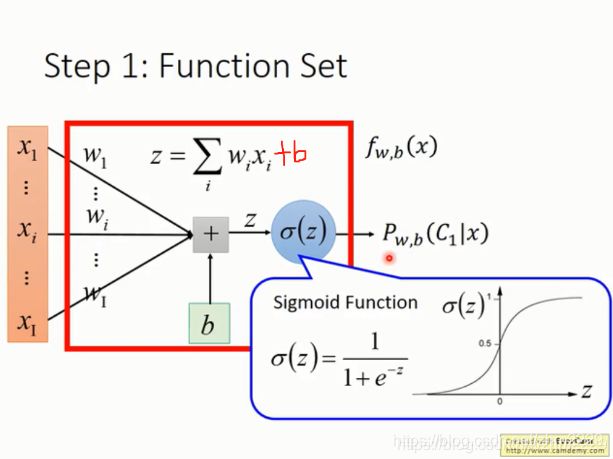
逻辑回归模型可以看成是将线性回归模型放入一个sigmoid函数中。
线性回归模型为
。
sigmoid函数是
。
所以逻辑回归模型函数是
。
sigmoid函数的范围为[0,1]，所以逻辑回归的输出范围也是[0,1]，它相当于是x属于某个类别的概率。
损失函数
假设有下面这些训练数据，他们属于两个类别c1和c2. 我们要用一个模型f(x) 去拟合这批数据，使每个数据属于它的类别的概率最大。由于函数f(x)是关于weights w和bias b 的函数，所以模型的训练过程就是找一个最合适的w和b能使总概率最大。
由于只有两个类别，为了方面计算，我们将c1和c2分别用1和0来表示。
另外，求总概率
的最大值相当于求
的最小值。当替换掉之后，可得到下图中的结果。
由于类别只有0和1，所以可以用
来替代原来式子。
这样就得到了逻辑回归模型的损失函数：
它相当于两个伯努利分布的交叉熵cross entropy。所以逻辑回归的损失函数叫cross entropy或者log loss function。
cross entropy的定义如下：
损失函数和错误函数的区别是：loss function是指一个数据上的错误。error function是一批数据上的平均错误
当真实类别y=1时，损失函数为-logf(x),它的图像如下。 可以看到预测值f(x)=0时，损失函数最大，当预测值f(x)=1时，损失函数最小。
当真实类别y=0时，损失函数为-log(1-f(x)), 它的损失函数在f(x)=1时最大，在f(x)=y=0时最小。
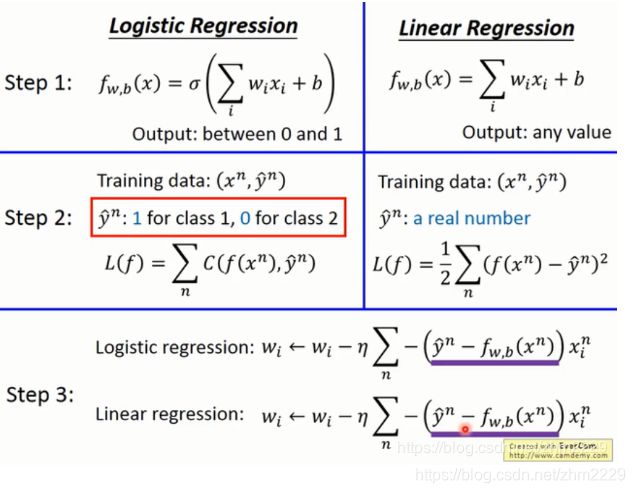
可以得到逻辑回归和线性回归的模型函数及损失函数的对比如下：
为什么线性函数可以用真实label和预测label之间差值的平方作为损失函数，而逻辑回归不用这个呢？这个后面再解释。
学习算法
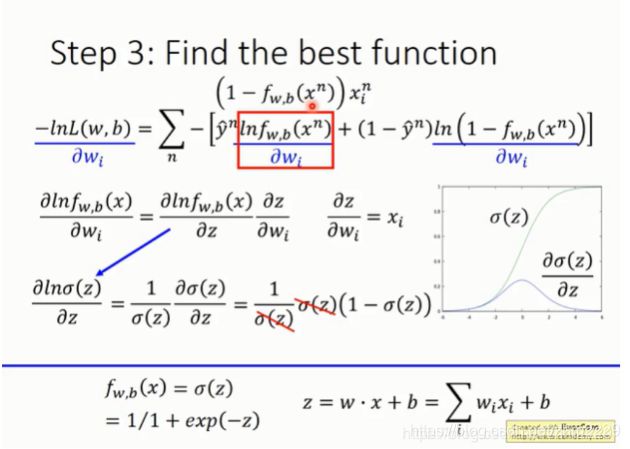
接下来，就是怎么求损失函数的最小值。由于我们最终要得到的是weight和bias的值，所以我们用损失函数对他们求偏导。
对于复合函数，用链式法则求导。
由于中间涉及到sigmoid函数的求导，所以先给出sigmoid函数的导数如下：
其他部分利用链式法则逐层求导。
最后得到
。
根据梯度下降对权重w进行更新，更新公式如上图。
它由3个因素决定：learning rate，数据xi，以及预测值和实际值的差值大小。
逻辑回归的模型函数，损失函数，学习算法以及它与线性回归模型的对比如下。
逻辑回归解决多分类问题
由上面可知，逻辑回归只适用于二分类问题，类别要么是0，要么是1.
当然，如果要用逻辑回归处理多分类问题也可以，一般可以用有三种方法：一种是将一个类别设为1，其他所有类别设为0，训练多个二分类分类器，然后选择概率最高的分类器，它的预测类别就是所要的类别。但是会造成数据集不平衡。第二种是每次只取两个类别的数据进行训练。训练多个分类器，最后通过多个分类器投票选择出最后的类别。但是当类别较多时需要的分类器数量较多
，影响运行速度。第三个是使用softmax函数。
下面介绍softmax方法。
softmax函数能将一个含任意实数的K维向量“压缩”到另一个K维实向量，使得每一个元素的范围都在(0,1)之间，并且所有元素的和为1。softmax函数定义如下
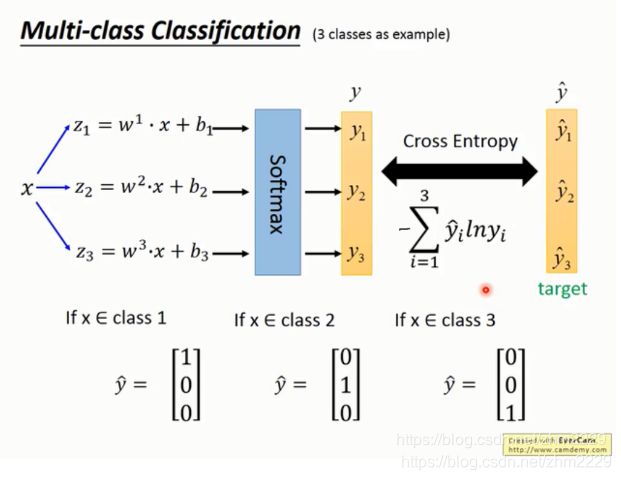
softmax 方法如下图所示。
假设有3个类别C1,C2,C3。 针对这3个类别分别训练3个线性模型z1,z2,z3。当有一个新的数据x过来时，z1,z2,z3都会产生一个输出。这3个输出被输入softmax函数，得到y1，y2,y3三个概率。表示x属于类别c1, c2, c3的概率分别是多少。
然后再将预测的y1，y2,y3和实际的类别标签
做cross entropy 运行，这是模型的损失函数。然后用相同的方法求损失函数的最小值，获得w和b的最优解。
逻辑回归为什么要用cross entropy 来计算loss，而不像linear regression一样用平方差来计算loss
当我们用差值的平方做损失函数求导时，如下图所示。假如真实类别为1，如果预测类别也为1，两者很相近，导数为0，符合预期。但是当预测类别为0时，它和真实类别相差很大，但是导数也为0，这显然是有问题的。同样在真实类别为0时也会发生这样的问题。所以不选用差值的平方作为损失函数。
cross entropy和square error 在逻辑回归上的loss和weights的图像如下。如果使用红色的平方差，loss是很平坦的，导数就很小，那么参数更新就很慢。这时我们也不能通过增大learning rate来加速参数更新，因为这时有可能就是预测值和目标值很接近的时候，如果learning rate过大，就跳过最优解了。
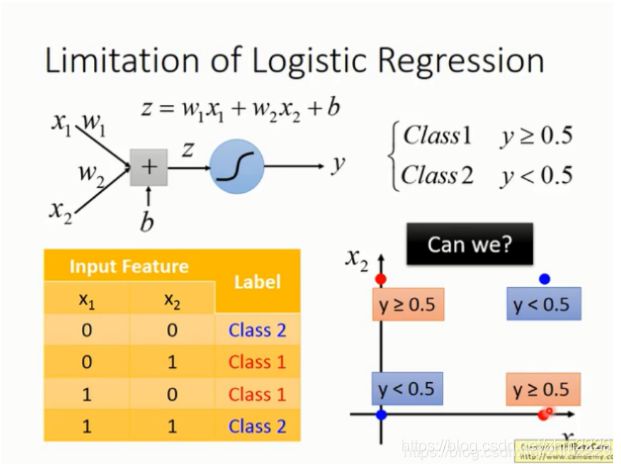
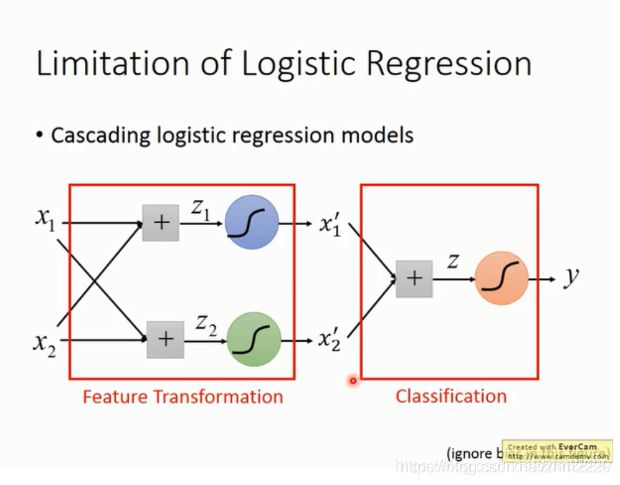
logistic regression的局限
由于逻辑回归是线性分类器，它是用一条直线对类别进行划分。但是在下面的图中，没有一条直线可以将红色的点和蓝色的点分开。
解决的方法是feature transfermation。
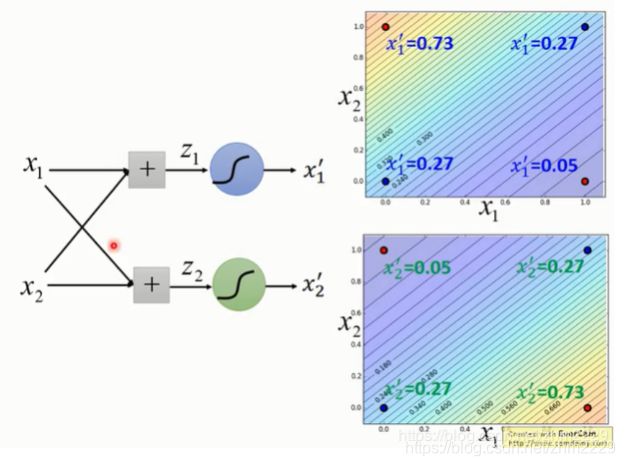
比如将特征x1，x2改为到点(0,0)和点(1,1)的距离，那么这些数据点就可以转换成了右边的图，则可以用直线进行线性划分了。
但是怎么制造特征转换比较麻烦，可以考虑让机器完成这个工作。我们可以将多个逻辑回归叠起来一起用。
这样就可以用逻辑回归将这样的数据进行划分了。
当把多个逻辑回归模型叠加起来，就成了神经网络，其中每一个逻辑回归模型就是一个神经元。
参考资料：
李宏毅机器学习视频：https://www.bilibili.com/video/av27639681/?p=10