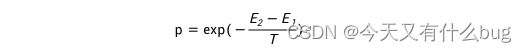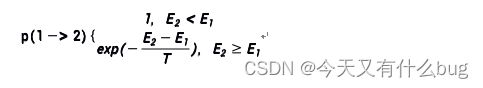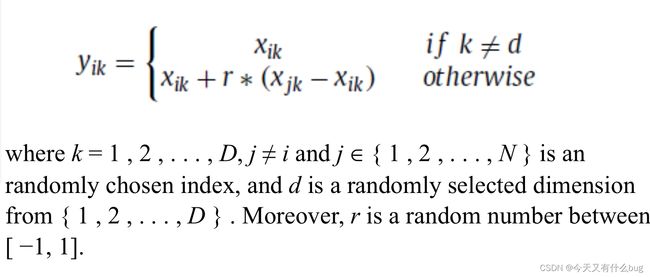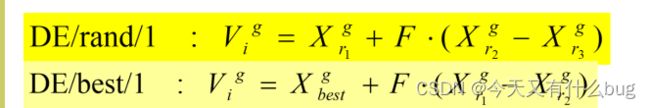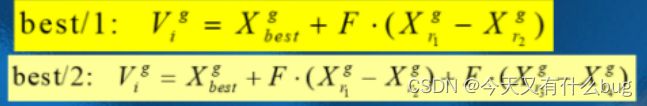智能优化算法期末复习

目录

一、GA遗传算法

二、ACO蚁群算法

三、PSO粒子群算法

 四、SA模拟退火算法

五、ABC人工蜂群算法

六、DE差分进化算法

七、TA阈值接收算法 

 八、综合

---

一、GA遗传算法

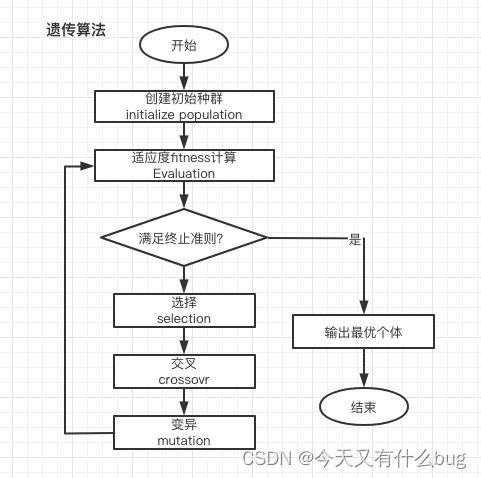
1.运算流程

2.遗传算法适应值分配策略（基于目标函数的直接分配、基于排名的分配）

3.遗传算法在二进制问题（如0-1背包）和顺序问题（如TSP问题）的交叉和变异算子的实现

（1）单点交叉

左边部分都不变。

（2）部分交叉

现将所交叉部分提取出来，交换。剩下的根据情况分析是否放原位。

（3）变异：

0-1背包问题：直接0—>1，1—>0

TSP问题：

swap： 断掉4条边，连上4条边。

insert： 断掉一部分，将该部分插入某处。

inverse：将某一部分进行翻转，还是放在原处。

4.遗传算法的交叉概率和变异概率对算法行为的影响

①交叉概率Pc：较大的交叉概率可以增强遗传算法开辟新的搜索区域的能力，但高性能的模式遭到破坏的可能性增大；若交叉概率太低，遗传算法搜索可能陷入迟钝状态。

②变异概率Pm：一般低频度的变异可防止群体中重要基因的可能丢失，高频度的变异将使遗传算法趋于纯粹的随机搜索。

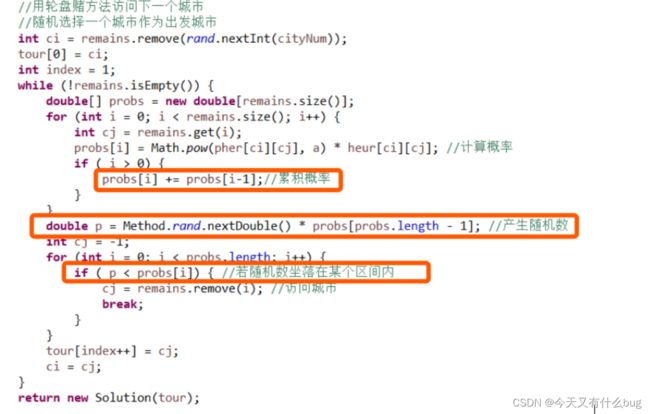
  5.轮盘赌思想算法实现（遗传算法）

二、ACO蚁群算法

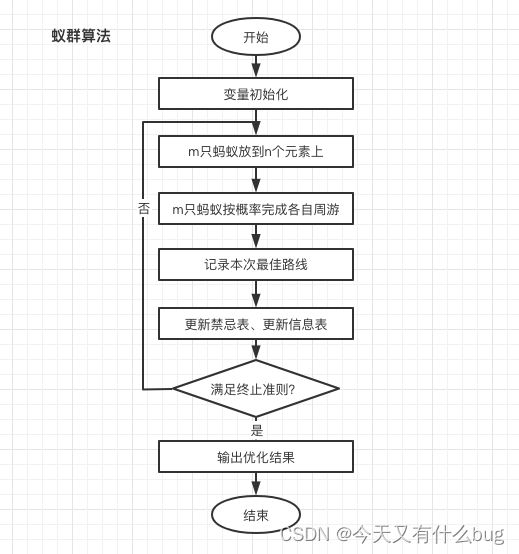
1.运算流程

2. 蚁群优化算法的信息素挥发系数对算法性能的影响

 ρ表示信息素挥发系数，它反映了蚂蚁群体中个体之间相互影响的强弱。

当ρ过小时，则表示以前搜索过的路径上被再次选择的可能性过大，算法的随机搜索性能和全局搜索能力会变弱。

当ρ过大，说明路径上的信息素挥发相对变多，算法的随机搜索性能和全局搜索能力得到提高，但会增加过多无用的搜索操作导致算法收敛速度降低。

3.从信息素挥发和沉积的角度分析蚁群优化算法的正反馈机制

某条路径上信息素挥发越多，剩余信息素越少，后续蚁群访问的概率就越小。从而该条路径上信息素也越少，后续蚁群访问的概率继续减小，形成正反馈机制。

相反，若路径上信息素挥发越少，剩余信息素越多，后续蚁群访问的概率就越大。从而该路径上信息素就越多，后续蚁群访问概率增大，形成正反馈机制。

3.蚂蚁算法的概率公式

三、PSO粒子群算法

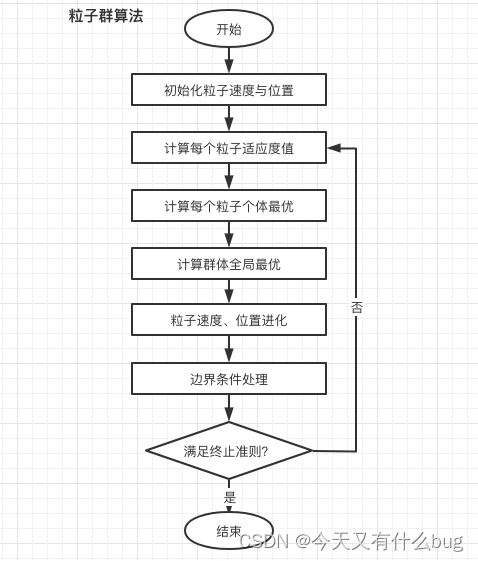
1.运算流程

2.粒子群优化算法的惯性权重w对算法的影响

可以同来控制算法的开发和探索能力。惯性权重的大小表示了对粒子当前速度继承的多少。当惯性权重较大时，全局寻优能力较强，局部寻优能力较弱。当惯性权重较小时，全局寻优能力较弱，局部局部寻优能力较强。

3.PSO算法的速度和位置修改公式

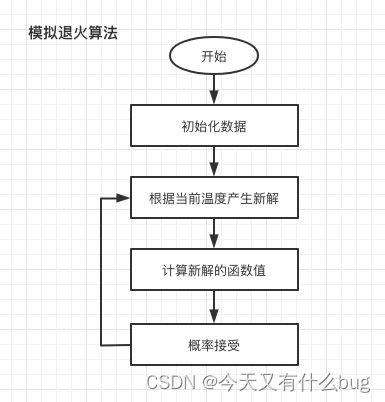
 四、SA模拟退火算法

1.运算流程

 2.模拟退火算法的的概率接收公式

系统从能量E1变化到E2，其对应的概率为：

 如果E2＜E1，系统接收此状态；否则，以一个随机的概率接收或丢弃此状态。状态2被接收的概率为：

注：公式

中的负号是求最小值的时候才有，若问题时求最大值，那么就没有负号，要懂得区别

3. 模拟退火算法的初始温度和降温系数（假设是几何降温）对算法行为的影响

（1）初始温度T0:T0越大，获得高质量解的概率越大。但是初温过高会导致计算时间增加，降低算法的收敛速度。

（2）降温速度α ：α是[0,1]且非常接近1的常数，降温系数越大，温度下降越慢，算法收敛速度越慢，接收劣质解的概率越高，获得高质量解的概率越高。

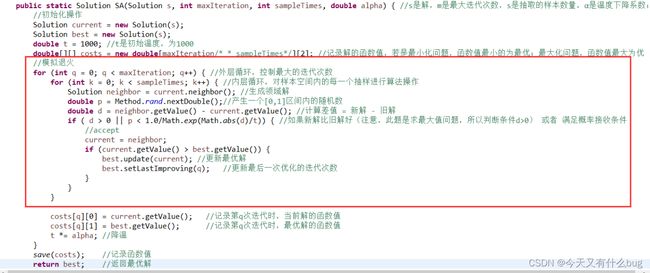
4.模拟退火算法解决0-1背包问题

 

五、ABC人工蜂群算法

1.侦察蜂scout和观察蜂onlooker的作用

（1）侦察蜂的作用：当雇佣蜂太久没有更新解时（即陷入了局部解），则启动侦察蜂重新进行全局搜索，从而避免算法陷入局部最优解。

（2）观察蜂（跟随蜂）的作用：对雇佣蜂找到的局部解周围进行探索，即对局部解进行优化，寻找更优的局部最优解。

2.ABC算法的雇佣蜂（Employed bee）和观察峰（Onlooker）的数量对算法性能的影响。

①雇佣蜂（采蜜蜂）的数量越多，算法全局搜索性能越强，算法收敛越慢，但搜索到全局最优解的可能越大；

②观察蜂（跟随蜂）的数量越多，算法局部搜索性能越强，算法收敛越快，但越容易陷入局部最优解。

3.ABC算法的位置修改公式

 4.从观察蜂的工作机制分析蜂群优化算法的正反馈机制。

观察蜂是跟随雇佣蜂，雇佣蜂找的蜜源越好，就会有越多的观察蜂跟随它，而观察蜂跟随的越多，那对雇佣蜂的函数值寻优次数（对蜜源的优化）就越多，那找到的解（蜜源）就会更优。从而形成了正反馈。

六、DE差分进化算法

1.算法流程

2.差分进化算法参数f对算法性能的影响

变异算子f∈[0,2]是一个实常数因数，它决定偏差向量的缩放比例。

变异算子f过小，则可能造成算法“早熟”。随着f值的增大，防止算法陷入局部最优的能力增强，但当f ＞ 1时，算法收敛到最优值的速度会变慢（这是因为当差分向量的扰动大于两个个体之间的距离时，种群的收敛性会变得很差）。通常f取0.5。

3.差分进化算法参数交叉概率cr对算法性能的影响

交叉算子cr是一个范围在[0,1]内的实数，它控制着一个试验向量参数来自随机选择的变异向量而不是原来向量的概率。交叉算子cr越大，发生交叉的可能性就越大。cr一个较好的取值是0.1，但较大的cr通常会减慢算法的收敛，为了看看是否可能获得一个快速解，可以先尝试cr=0.9或cr=1.0。

4.DE算法的base vector、difference vector、donor vector、trial vector和target vector

（1）base vector：基向量；

（2）difference vector：差向量（又叫偏差变量），两个不同基向量的差；

（3）donor vector：变异向量，产生变异的向量；

（4）trial vector：试验向量，引入交叉操作后的向量组，如果试验成功，则取代原有的目标向量；试验失败，则继承原有的目标向量；

（5）target vector：目标向量，实际所需的解。

5. DE算法的mutation公式DE/rand/1、DE/best/1

  

6. DE的两种交叉策略bin和exp

 bin是均匀交叉，exp是指数交叉。

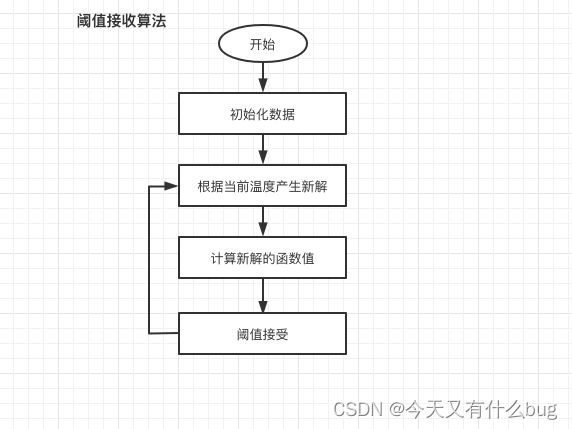
七、TA阈值接收算法 

1.算法流程

（类似于模拟退火算法，只是将概率接受改成了阈值接收）

2.阈值接收方法的初始阈值和阈值下降系数（假设是几何降温）对算法行为的影响

（与模拟退火的初始温度和降温系数类似）

初始阈值越大，接收劣质解的概率越高，获得高质量解的概率就越大，然而，初始阈值过高会使计算时间增加，降低算法的收敛速度。

阈值下降系数越大（即越接近1），阈值下降越慢，算法收敛速度越慢，接收劣质解的概率越高，获得高质量的解的概率就越高。

 八、综合

1.区分metaheuristic和heuristic

（1）metaheuristic：元启发式算法，是一个通用的启发式策略，不借助于某种问题的特有条件，从而可以广泛运用。如GA、SA、PSO、ACO、ABC、DE。

（2）heuristic：启发式算法，针对特定条件下求解某个具体的问题。如爬山算法。

2.区分single solution-based和population-based的智能优化算法

（1）single solution-based的智能优化算法（迭代过程只有一个解）：SA、TA

（2）population-based的智能优化算法：GA、ABC、PSO、ACO、DE

3.区分construction-based和iterative improvement-based的智能优化算法

（1）construction-based（每次都是从头开始构造新解）：ACO解是通过一步步选出来的

（2）iterative improvement-based（迭代产生新解）：GA、ABC、PSO、SA、DE、TA

4.区分组合优化问题、连续优化问题、约束优化问题等概念及我们使用的实例

（1）组合优化问题

①概念：具有离散变量的问题，我们称它为组合的。组合优化（Combinatorial Optimization）问题的目标是从组合问题的可行解集中求出最优解。

②实例：旅行商问题（Traveling Salesman Problem－TSP）、0-1背包问题（Knapsack Problem——KP）、度约束的最小生成树问题；

（2）连续优化问题

①概念：连续优化是求解连续变量的问题，其一般是求解一组实数，或者一个函数。

②实例：求解函数的最大值和最小值

（3）约束优化问题

①概念：约束优化问题是一类数学最优化问题，它由目标函数以及与目标函数中的变量相关的约束条件两部分组成，优化过程则为在约束条件下最优化（最大化或最小化）目标函数。

②实例：0-1KP、目标规划、度约束的问题

5.算法的简写

（1）模拟退火算法：Simulated Annealing，简称SA

（2）遗传算法：Genetic Algorithm，简称GA

（3）阈值接收算法：Threshold Algorithm，简称TA

（4）粒子群算法：Particle Swarm Optimization，简称PSO

（5）蚁群优化算法（简称蚁群算法）：Ant Colony Optimization，简称ACO

（6）人工蜂群算法（简称蜂群算法）：Artificial Bee Colony Algorithm, 简称ABC

（7）差分进化算法：Differential Evolution，简称DE

6.各种算法接收新解的方式（接收所有，只接收更好的，概率接收）

（1）概率接收劣质解：模拟退火算法（SA）、阈值接收算法（TA，确定性接收）

（2）只接收更好的：遗传算法（GA）、差分进化算法（DE）、人工蚁群优化算法（ACO）、蜂群优化算法（ABC）

（3）接收所有：粒子群优化算法（PSO）

7.根据产生新解时修改的维数和接受新解的策略比较粒子群优化算法、差分进化算法和蜂群优化算法

算法	产生新解时修改的维数	接受新解的策略
PCO	n维	接受所有的解，通过比较适应度值，迭代更新粒子的速度和位置，从而逐步收敛于全局最优解
DE	1～n维（由概率公式决定）	只接受更好的解
ABC	1维（修改方向）	只接受更好的解，通过雇佣蜂全局搜索、跟随蜂进行局部优化以及侦查蜂辅助全局搜索的机制，算法逐步收敛于全局最优解

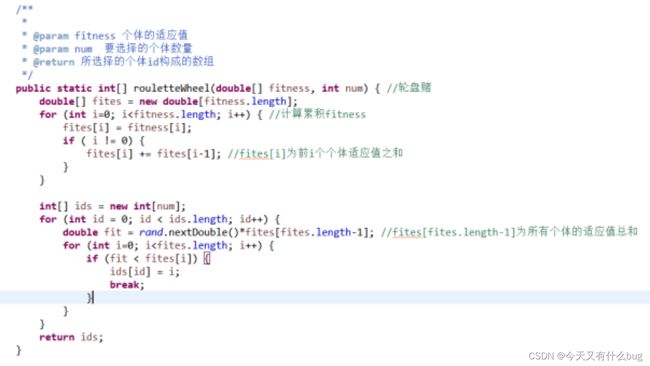
8.遗传算法中轮盘赌思想的具体实现

public static int[] rouletteWheel(double[] fitness, int num){
        double[] fites = new double[fitness.length];
        for(int i = 0;i < fites.length; i++){
            fites[i] = fitness[i];
            if( i != 0){
                fites[i] += fites[i-1];
            }
        }
        int[] ids = new int[num];
        for (int id = 0; id

9.随机键表示法将连续型数据转换为城市访问路径的方式 

10.将连续性数据转换为二进制数据、整型数据的方法

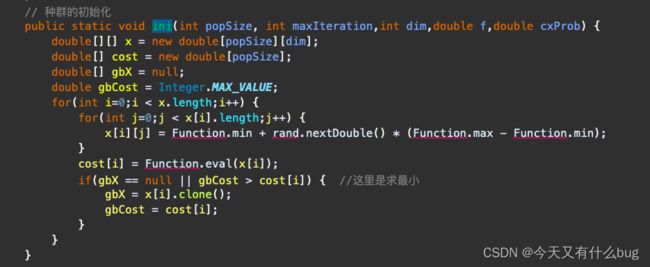
11.基于种群的元启发式的初始化过程 

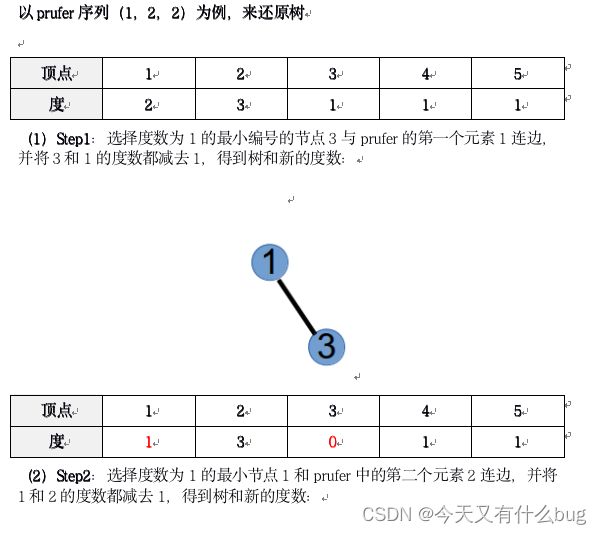
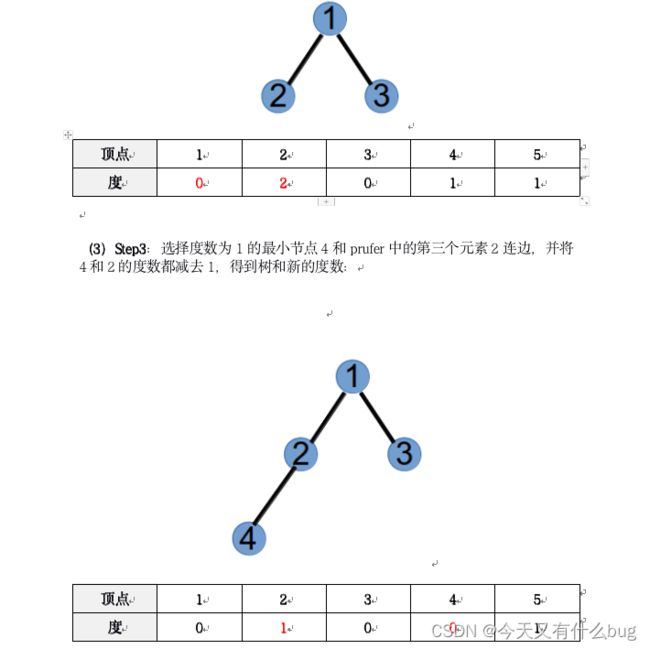
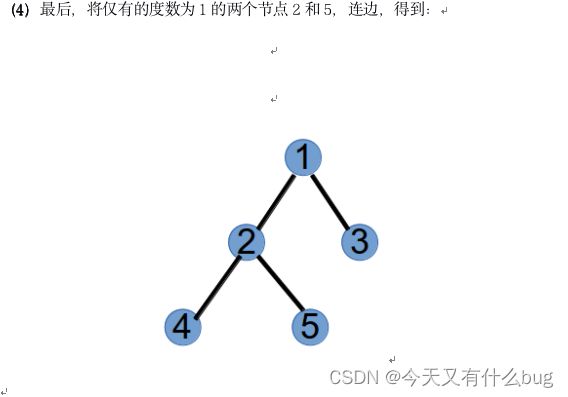
12.prufer序列转换为边集表示的树

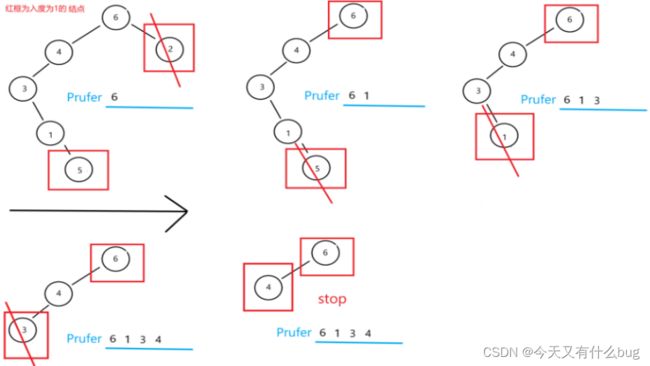
13.将树转化为prufer序列 

（1）概念：prufer序列是无根树转化而来的序列。对树的每个节点进行1到n的编号，则点数为n的树转化来的Prufer数列长度为n - 2。

（2）Prufer序列 -> Tree树

方法：

① 找到编号最小的叶子x

② 设与叶子x相连的点是y，则删掉x，并在prufer序列尾部加入一个数y

③ 重复1,2操作，直到整棵树只剩下两个节点，此时prufer序列长度为n - 2。

============================== 

到此为止，不会再更新了。

逢考必过～