使用PyTorch构建神经网络(详细步骤讲解+注释版) 03 模型评价与准确率提升
文章目录
- 1 使用模型预测数据
- 2 模型效果评价
- 3 模型效果提升
-
- 3.1 优化损失函数
- 3.2 激活函数
- 3.3 权重更新方法优化
上一节我们已经成功训练了一个神经网络模型
使用PyTorch构建神经网络(详细步骤讲解+注释版) 02-数据读取与训练
本文的使用的部分类方法为前述文章定义所得,如果希望运行完整代码建议同时查看上一篇文章或文末留言发你完整代码。
1 使用模型预测数据
这里我们使用mnist的训练集
mnist_test = MnistDataset('你的mnist_test.csv地址')
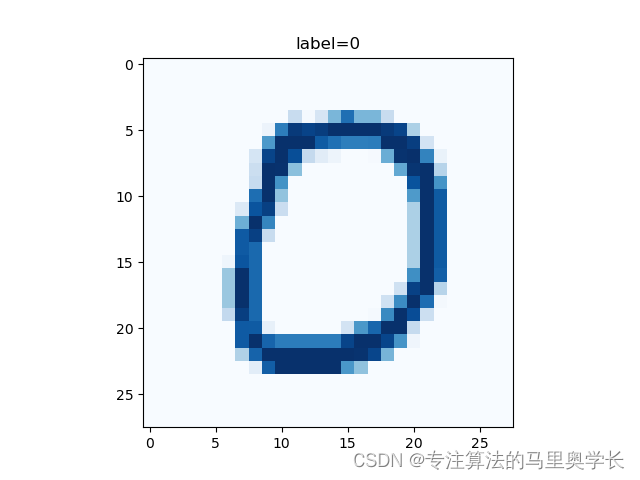
随便传入一行数据,这里我们使用第10行数据,使用前面定义的plot_image方法看一下数据有没有问题,可以看到这幅图是一个手写的0。
index = 9 # 用第10幅图像试一下
mnist_test.plot_image(index)
output_10 = C.forward(mnist_test[index][1])
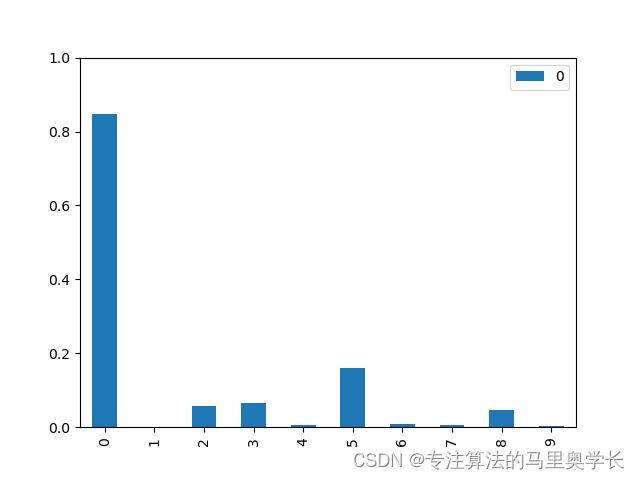
此时我们就获得了一个张量形式的输出,为了将这个输出可视化出来,我们可以先将其解析成一个numpy数组,再转换成我们熟悉的dateframe格式,这时这组数据就可以被可视化了。
output_10_pd = pandas.DataFrame(output_10.detach().numpy())
output_10_pd.plot(kind='bar', ylim=(0,1))
plt.show()
可以看到,尽管其他的输出节点并不是非常的接近0,但模型对这组数据还是得出了正确的预测结果。
2 模型效果评价
在不调包的情况下,我们可以简单的统计以下分类的正确率。
score = 0
items = 0
for label, image_data_tensor, target_tensor in mnist_dataset:
answer = C.forward(image_data_tensor).detach().numpy()
if answer.argmax() == label:
score += 1
items += 1
print('一共有{}个样本'.format(items))
print('预测正确{}个'.format(score))
print('准确率是{:.2f}%'.format((score/items)*100))
其中argmax是判断数组中最大值所对应的索引,也就是判断神经网络预测的结果是什么。当预测结果正确时,得分+1。
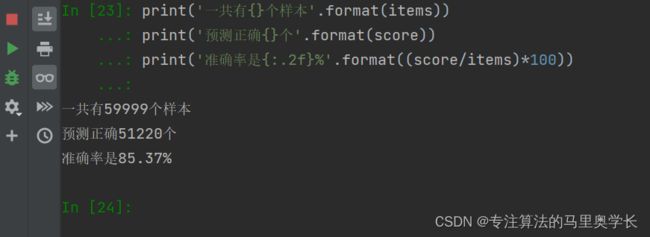
在仅仅使用三层的最简单的神经网络的情况下,可以看出依然是一个不错的结果。
3 模型效果提升
提升模型效果的方法有很多,比如增加层数,优化损失函数,优化激活函数,优化学习方法等等。
3.1 优化损失函数
在之前的定义中,我们使用的损失函数是MSE,这是一个最常用的损失函数(大概没有之一)。但对分类问题,我们还要其他可选的方法。(无论是回归还是分类,都很难说最佳的方法是什么,需要结合数据类型以及我们建模的目的来确定)在这里我们可以尝试使用BCELoss函数来代替MSELoss函数。
BCELoss(二值交叉熵损失函数)的计算原理是在二元分类任务中使用的。它的计算方式是将真实标签 y y y 与预测标签 y ^ ŷ y^ 的交叉熵作为损失函数。
B C E L o s s = − ( y log ( y ^ ) + ( 1 − y ) log ( 1 − y ^ ) ) BCELoss = -(y\log(ŷ) + (1-y)\log(1-ŷ)) BCELoss=−(ylog(y^)+(1−y)log(1−y^))
其中, y y y 是真实标签, y ^ ŷ y^ 是预测标签的概率。对于每一个样本,我们都会得到一个 B C E L o s s BCELoss BCELoss 值,最后再将所有样本的 B C E L o s s BCELoss BCELoss 值取平均值作为最终的损失值。这个损失函数的值越小,模型的预测结果就越准确。
class Classifier(nn.Module):
# 初始化PyTorch父类
def __init__(self):
super().__init__()
# 创建损失函数
self.loss_function = nn.BCELoss()
大家可以自行尝试修改后对模型预测准确性的影响。同时,还有一些其他常见的损失函数,比如:nn.CrossEntropyLoss: 交叉熵损失函数, 常用于分类问题;nn.NLLLoss: 对数似然损失函数, 常用于自然语言处理中的序列标注问题;nn.L1Loss: L1 范数损失函数, 常用于稀疏性正则化等等。
3.2 激活函数
之前我们使用的是最常见的Sigmoid函数,其计算方法为:
S i g m o i d ( x ) = 1 1 + e − x Sigmoid(x)=\frac{1}{1+e^{-x}} Sigmoid(x)=1+e−x1
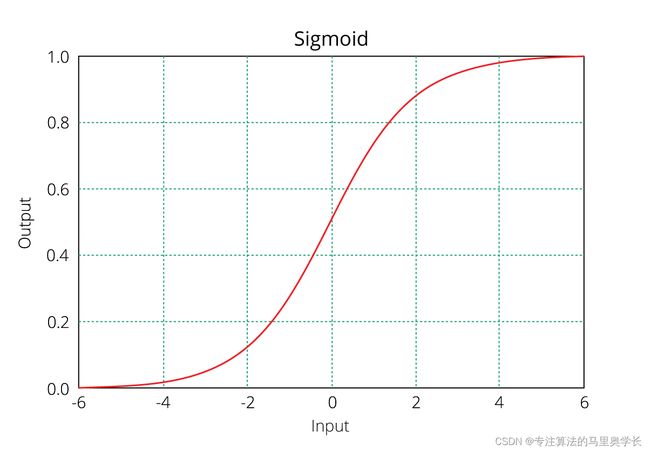
但Sigmoid也有一些局限性,首先是不能处理好多分类问题(前面我们是把多分类问题变成了10个二分类问题来求解);其次是对样本不平衡问题也不太适用(好在我们这个数据集是样本均衡的);最后Sigmoid存在饱和区间,也就是在非常大和非常小的区域内,函数的梯度基本为零,这就使训练变得慢了。
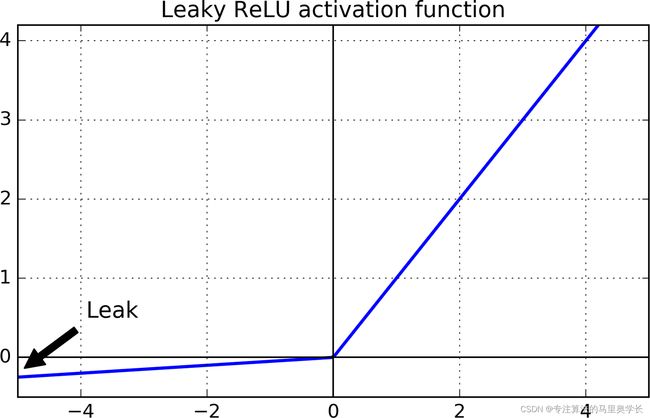
另一种常用的损失函数是Leaky ReLU(Rectified linear unit)。
Leaky ReLU是一种非常流行的激活函数,它在 ReLU 的基础上进行了扩展,用于解决 ReLU 在训练中所面临的"dying ReLU"问题。
ReLU 函数只保留正数部分,对于负数部分直接归零。这样做的好处是可以有效地防止梯度消失,使得神经网络的训练变得更快。但是,如果一个神经元的输入总是小于零,那么它的权重就永远不会更新,这个神经元就被称为"dead ReLU"。这种情况可能会导致整个神经网络的性能降低。
Leaky ReLU 解决了这个问题,它在负数部分也允许一定的输出,这样即使输入是负数,权重也有机会得到更新。
Leaky ReLU的计算公式为:
f ( x ) = { x if x ≥ 0 a x if x < 0 f(x) = \begin{cases} x & \text{ if } x \geq 0 \\ ax & \text{ if } x < 0 \end{cases} f(x)={xax if x≥0 if x<0
其中 a a a 为常数, 一般取 0.01 0.01 0.01 或者 0.1 0.1 0.1.
同样如果希望在模型中使用这个损失函数,可以对代码做出简单的修改。
class Classifier(nn.Module):
# 初始化PyTorch父类
def __init__(self):
super().__init__()
# 定义网格结构
self.model = nn.Sequential(
nn.Linear(784, 200),
nn.LeakyReLU(),
nn.Linear(200, 10),
nn.LeakyReLU()
3.3 权重更新方法优化
在模型中我们使用的是SGD(Stochastic Gradient Descent)权重更新方法。但这一方法容易让模型陷入局部最优点,也就是梯度为零的极值点而不是最值点。
为了解决这一问题,可以尝试使用Adam方法。Adam(Adaptive Moment Estimation)是一种流行的用于深度学习的优化器。它的工作原理是在梯度下降的基础上引入了动量,并且对每个参数都维护了两个变量:指数加权移动平均值和指数加权移动平均方差。这样做的好处是可以在一定程度上缓解梯度消失或爆炸的问题,并且能够自动调整学习率,使其适应不同的参数。
如果希望详细了解这部分内容,为大家提供Adam优化器的更新公式,如不需要直接跳转到后续内容即可:
g t = ∇ θ J ( θ ) g_t = \nabla_\theta J(\theta) gt=∇θJ(θ)
m t = β 1 m t − 1 + ( 1 − β 1 ) g t m_t = \beta_1 m_{t-1} + (1 - \beta_1) g_t mt=β1mt−1+(1−β1)gt
v t = β 2 v t − 1 + ( 1 − β 2 ) g t 2 v_t = \beta_2 v_{t-1} + (1 - \beta_2) g_t^2 vt=β2vt−1+(1−β2)gt2
m t ^ = m t 1 − β 1 t \hat{m_t} = \frac{m_t}{1 - \beta_1^t} mt^=1−β1tmt
v t ^ = v t 1 − β 2 t \hat{v_t} = \frac{v_t}{1 - \beta_2^t} vt^=1−β2tvt
θ t = θ t − 1 − α v t ^ + ϵ m t ^ \theta_t = \theta_{t-1} - \frac{\alpha}{\sqrt{\hat{v_t}} + \epsilon} \hat{m_t} θt=θt−1−vt^+ϵαmt^
t t t 表示时间步
g t g_t gt 表示当前时间步损失函数的梯度
m t m_t mt 表示当前时间步的动量
v t v_t vt 表示当前时间步的RMSProp算法中的平方梯度积累
m t ^ \hat{m_t} mt^ 表示当前时间步的校正后的动量
v t ^ \hat{v_t} vt^ 表示当前时间步的校正后的平方梯度积累
α \alpha α 表示学习率
β 1 \beta_1 β1 和 β 2 \beta_2 β2 是两个超参数,通常取值为 0.9 0.9 0.9 和 0.999 0.999 0.999
ϵ \epsilon ϵ 是一个很小的常数,通常取 1 0 − 8 10^{-8} 10−8,用于给平方根加一个偏移量,以防止分母为 0 0 0 的情况发生
在实际使用中,通常需要为每个参数 θ \theta θ 分别维护一个 m t m_t mt 和 v t v_t vt,然后分别计算每个参数的更新值
class Classifier(nn.Module):
# 初始化PyTorch父类
def __init__(self):
super().__init__()
# 创建优化器
self.optimiser = torch.optim.Adam(self.parameters())
对于完整的经典代码与完整的修改后优化代码,均可评论区留言获取或者我上传的资源中进行下载。完整代码下载链接