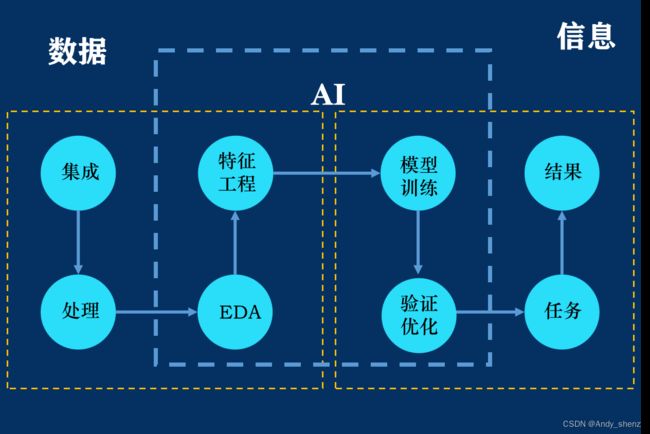
特征工程原理（一）

一、定义

在机器学习原理中讲过机器学习的基本流程，其中很重要的一个环节就是特征工程。

1.1 基本概念

特征工程（Feature Engineering）：从原始数据中提取特征的过程，这些特征可以很好地描述数据，并且利用特征建立的模型在未知数据上的性能表现可以达到最优（或者性能最佳）。

• 是将原始数据转化成更好的表达问题本质的特征的过程，使得将这些特征运用到预测模型中能提高对不可见数据的模型预测精度。
• 可以理解为就是发现对因变量y有明显影响作用的特征，通常称自变量x为特征，特征工程的目的是发现重要特征。
• 目的：如何能够分解和聚合原始数据，以更好的表达问题的本质。

1.2 意义

1. 灵活性越强

   好特征的灵活性在于允许你选择不复杂的模型，同时运行速度也更快，更容易理解和维护

2. 构建的模型越简单

   好的特征不需要花太多的时间去寻找最有效的参数，这大大降低了模型的复杂度

3. 模型的性能越出色

   特征工程的最终目的是提升模型的性能

二、特征处理

特征提取之前需要对数据进行预处理

2.1 数据采集

数据采集(DAQ)： 又称数据获取，是指从传感器和其它待测设备等模拟和数字被测单元中自动采集信息的过程

数据采集一般是有线上行为数据和内容数据两种

• 线上行为数据：页面数据、交互数据、表单数据、会话数据等。
• 内容数据：应用日志、电子文档、机器数据、语音数据、社交媒体数据等。

2.2 数据清洗

数据清洗(Data cleaning)： 对数据进行重新审查和校验的过程，目的在于删除重复信息、纠正存在的错误，并提供数据一致性。
数据清洗一般包括，逻辑错误清洗、缺失值、异常值、格式内容等的处理

逻辑错误清洗：重复值、不合理数据（2岁的孩子学历为大学）
缺失值：删除或者填充【特殊值填充、模型预测填充、插值填充等】
异常值：检测【统计分析等】、光滑处理【数据分箱、回归】、删除、不处理【有些模型可以自动处理异常值】
格式内容：时间日期数据、全角半角、特殊字符等等

2.3 数据采样

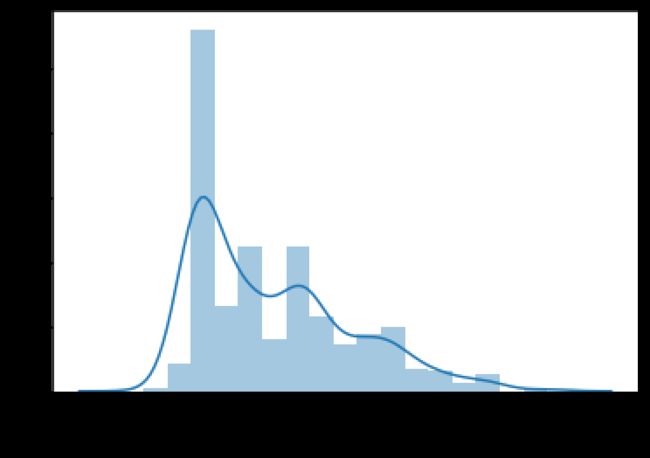
样本类别分布不均衡：不同类别的样本量差异非常大

样本不均衡指的是给定数据集中有的类别数据多，有的数据类别少，且数据占比较多的数据类别样本与占比较小的数据类别样本两者之间达到较大的比例。
。即使得到分类模型，也容易产生过度依赖于有限的数据样本而导致过拟合的问题。当模型应用到新的数据上时，模型的准确性和健壮性将很差。

影响：样本分布不均衡将导致样本量少的分类所包含的特征过少，并很难从中提取规律。

采样方法：

上采样（over-sampling），通过增加分类样本量较少的样本来实现均衡，如直接复制少数样本增加记录，缺点是可能会导致过拟合

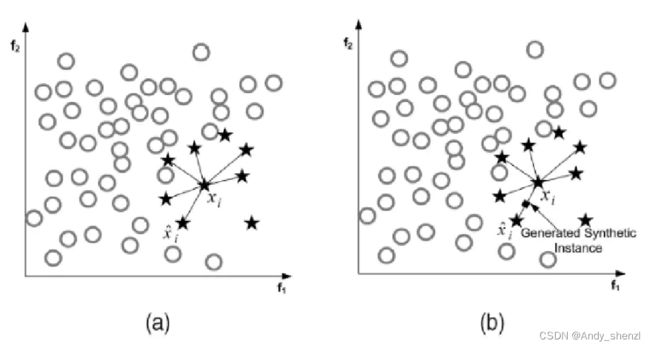
SMOTE（Synthetic Minority Oversampling Technique），插值的方式加入近邻的数据点，合成少数类过采样技术。
基本思想：对少数类样本进行分析并根据少数类样本人工合成新样本添加到数据集中。
它是基于随机过采样算法的一种改进方案，由于随机过采样采取简单复制样本的策略来增加少数类样本，这样容易产生模型过拟合的问题，即使得模型学习到的信息过于特别(Specific)而不够泛化(General)
步骤：

1. 对于少数类中每一个样本x，以欧氏距离为标准计算它到少数类样本集中所有样本的距离，得到其k近邻。
2. 根据样本不平衡比例设置一个采样比例以确定采样倍率N，对于每一个少数类样本x，从其k近邻中随机选择若干个样本，假设选择的近邻为$x_n$。
3. 对于每一个随机选出的近邻$x_n$，分别与原样本按照如下的公式构建新的样本 $x_{new}=x+rand(0,1)\ast (x_n-x)$
   

下采样（under-sampling），通过减少分类样本量较多的样本来实现均衡，如直接删除样本，缺点是会丢失信息

三、特征转换

3.1 标准化

标准化是依照特征矩阵的列处理数据，及通过求标准分数的方法将特征转换为标准正太分布，并和整体样本分布相关；

$$x^{,}=\frac{x-\overline{x}}{S}$$

3.2 归一化

将样本的特征值转换到同一量纲下，把数据映射到【0,1】之间，适用于分布有明显边界的情况，受 outliner影响较大。
$$x^{,}=\frac{x-Min}{Max-Min}$$

3.3 二值化

针对定量特征
$$x^{,}=\{\begin{array}{ll}1,& \text{x > threshold}\\ 0,& \text{x <= threshold}\end{array}$$

3.4 亚编码

针对定性特征，是不能直接带入模型进行训练的，要转换成数值型才可以进行运算。

∣ 工人 （ 0 , 0 , 0 , 1 ） 农民 （ 0 , 0 , 1 , 0 ） 学生 （ 0 , 1 , 0 , 0 ） 职员 （ 1 , 0 , 0 , 0 ） ∣ \begin{vmatrix} 工人 & （0,0,0,1） \\ 农民 & （0,0,1,0） \\ 学生 & （0,1,0,0） \\ 职员 & （1,0,0,0） \\ \end{vmatrix} ​工人农民学生职员​（0,0,0,1）（0,0,1,0）（0,1,0,0）（1,0,0,0）​ ​

3.5 数据转化

数据转化主要是改变数据的分布，当数据不符合正态分布时需要将数据转换成正态分布，转换的方式比如：Log、指数、多项式等方法

原始数据

转换后

为什么需要转换为正态分布？
根据中心极限定理，将大量具有不同分布的随机变量加起来，所得到的新变量将最终具有正态分布。也就是说正态分布时随机分布，也就是去除了人工及其他的干扰后的分布，这样的分布在建立模型后就更容易预测；因为模型拟合的是数据本身的分布，没有其他因素的干扰，准确率会更高。