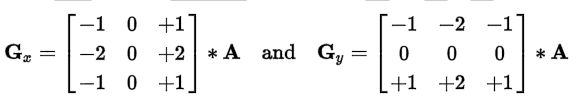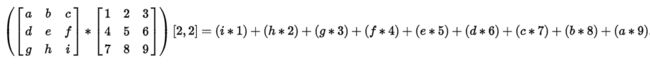图像卷积详细解释 常用卷积核解释说明

神经网络中的卷积层，它的原理就来源于图像卷积

概述

卷积在信号处理领域有极其广泛的应用, 也有严格的物理和数学定义. 本文只讨论卷积在数字图像处理中的应用.

在数字图像处理中, 有一种基本的处理方法:线性滤波. 待处理的平面数字图像可被看做一个大矩阵, 图像的每个像素对应着矩阵的每个元素, 假设我们平面的分辨率是 1024*768, 那么对应的大矩阵的行数= 1024, 列数=768.

用于滤波的是一个滤波器小矩阵(也叫卷积核), 滤波器小矩阵一般是个方阵, 也就是 行数 和 列数 相同, 比如常见的用于边缘检测的 Sobel 算子 就是两个 3*3 的小矩阵.

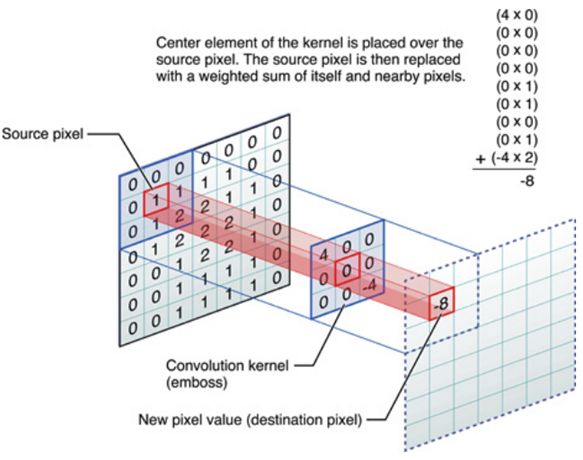
进行滤波就是对于大矩阵中的每个像素, 计算它周围像素和滤波器矩阵对应位置元素的乘积, 然后把结果相加到一起, 最终得到的值就作为该像素的新值, 这样就完成了一次滤波.

上面的处理过程可以参考这个示意图:

图像卷积计算示意图:

对图像大矩阵和滤波小矩阵对应位置元素相乘再求和的操作就叫卷积(Convolution)或协相关(Correlation).

协相关(Correlation)和卷积(Convolution)很类似, 两者唯一的差别就是卷积在计算前需要翻转卷积核, 而协相关则不需要翻转.

以 Sobel 算子为例

Sobel 算子 也叫 Sobel 滤波, 是两个 3*3 的矩阵, 主要用来计算图像中某一点在横向/纵向上的梯度, 看了不少网络上讲解 Sobel 算子 的文章, 发现人们常常把它的横向梯度矩阵和纵向梯度矩阵混淆. 这可能与 Sobel 算子 在它的两个主要应用场景中的不同用法有关.

Sobel 算子的两个梯度矩阵: Gx 和 Gy

这里以 Wiki 资料为准, Sobel 算子 有两个滤波矩阵: Gx 和 Gy, Gx 用来计算横向的梯度, Gy 用来计算纵向的梯度, 下图就是具体的滤波器:

 

• 注意:这里列出的这两个梯度矩阵对应于横向从左到右, 纵向从上到下的坐标轴, 也就是这种:

原点
O ------->  x轴
|
|
|
V  y轴

Sobel 算子的用途

它可以用来对图像进行边缘检测, 或者用来计算某个像素点的法线向量. 这里需要注意的是:

• 边缘检测时: Gx 用于检测纵向边缘, Gy 用于检测横向边缘.
• 计算法线时: Gx 用于计算法线的横向偏移, Gy 用于计算法线的纵向偏移.

计算展开

假设待处理图像的某个像素点周围的像素如下:

左上	上	右上
左	中心像素	右
左下	下	右下

那么用 Gx 计算展开为:

横向新值 = (-1)*[左上] + (-2)*[左] + (-1)*[左下] + 1*[右上] + 2*[右] + 1*[右下]

用 Gy 计算展开为:

纵向新值 = (-1)*[左上] + (-2)*[上] + (-1)*[右] + 1*[左下] + 2*[下] + 1*[右下]

前面说过, 做图像卷积时需要翻转卷积核, 但是我们上面的计算过程没有显式翻转, 这是因为 Sobel 算子 绕中心元素旋转 180 度后跟原来一样. 不过有些 卷积核 翻转后就变了, 下面我们详细说明如何翻转卷积核.

卷积核翻转

前面说过, 图像卷积计算, 需要先翻转卷积核, 也就是绕卷积核中心旋转 180度, 也可以分别沿两条对角线翻转两次, 还可以同时翻转行和列, 这3种处理都可以得到同样的结果.

对于第一种卷积核翻转方法, 一个简单的演示方法是把卷积核写在一张纸上, 用笔尖固定住中心元素, 旋转 180 度, 就看到翻转后的卷积核了.

下面演示后两种翻转方法, 示例如下:

假设原始卷积核为:

a	b	c
d	e	f
g	h	i

方法2:沿两条对角线分别翻转两次

先沿左下角到右上角的对角线翻转, 也就是 a和i, b和f, d和h交换位置, 结果为:

i	f	c
h	e	b
g	d	a

再沿左上角到右下角的对角线翻转, 最终用于计算的卷积核为:

i	h	g
f	e	d
c	b	a

方法3:同时翻转行和列

在 Wiki 中对这种翻转的描述:

convolution is the process of flipping both the rows and columns of the kernel and then multiplying locationally similar entries and summing.

也是把卷积核的行列同时翻转, 我们可以先翻转行, 把 a b c跟 g h i 互换位置, 结果为:

g	h	i
d	e	f
a	b	c

再翻转列, 把 g d a 和 i f c 互换位置, 结果为:

i	h	g
f	e	d
c	b	a

在 Wiki 中有一个计算展开式, 也说明了这种翻转:

 

• 注意:这里要跟矩阵乘法区分开, 这里只是借用了矩阵符号, 实际做的是对应项相乘, 再求和.

图像边缘像素的处理

以上都默认待处理的像素点周围都有像素, 但是实际上图像边缘的像素点周围的像素就不完整, 比如顶部的像素在它上方就没有像素点了, 而图像的四个角的像素点的相邻像素更少, 我们以一个图像矩阵为例:

左上角	...		...	右上角
...	...	...	...	...
左侧	...	...	...	右侧
...	...	...	...	...
左下角	...		...	右下角

位于左上角的像素点的周围就只有右侧和下方有相邻像素, 遇到这种情况, 就需要补全它所缺少的相邻像素，就是网络中的padding操作；

时域卷积 = 频域相乘

时域卷积 = 频域相乘

时域卷积 = 频域相乘

 

不同卷积核下卷积意义

我们经常能看到的，平滑，模糊，去燥，锐化，边缘提取等等工作，其实都可以通过卷积操作来完成，下面我们一一举例说明一下： 
（1）一个没有任何作用的卷积核：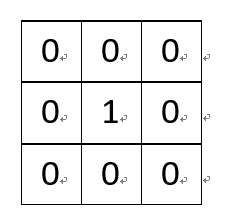 
 
将原像素中间像素值乘1，其余全部乘0，显然像素值不会发生任何变化。 
（2）平滑均值滤波： 
选择卷积核： 
 
该卷积核的作用在于取九个值的平均值代替中间像素值，所以起到的平滑的效果： 
 
 
（3）高斯平滑： 
卷积核： 
 
高斯平滑水平和垂直方向呈现高斯分布，更突出了中心点在像素平滑后的权重，相比于均值滤波而言，有着更好的平滑效果。 
 
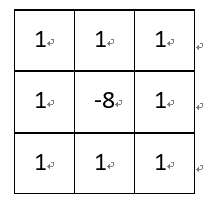
（4）图像锐化： 
卷积核：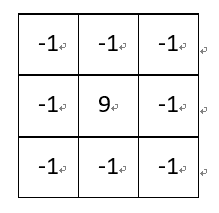 
 
该卷积利用的其实是图像中的边缘信息有着比周围像素更高的对比度，而经过卷积之后进一步增强了这种对比度，从而使图像显得棱角分明、画面清晰，起到锐化图像的效果。 
 
除了上述卷积核，边缘锐化还可以选择：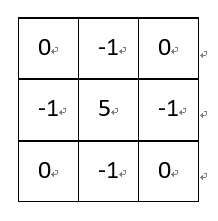 
 
（5）梯度Prewitt： 
水平梯度：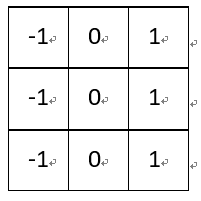 
 
 
垂直梯度：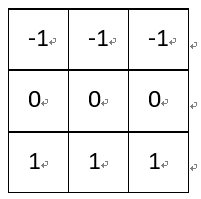 
 

梯度Prewitt卷积核与Soble卷积核的选定是类似的，都是对水平边缘或垂直边缘有比较好的检测效果。

（6）Soble边缘检测： 
Soble与上述卷积核不同之处在于，Soble更强调了和边缘相邻的像素点对边缘的影响。 
水平梯度：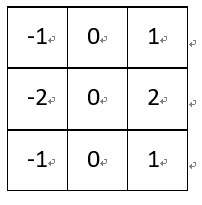 
 
 
垂直梯度：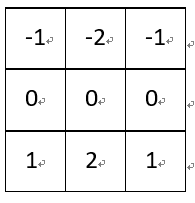 
 

以上的水平边缘与垂直边缘检测问题可以参考：Soble算子水平和垂直方向导数问题

（7）梯度Laplacian：

卷积核： 

Laplacian也是一种锐化方法，同时也可以做边缘检测，而且边缘检测的应用中并不局限于水平方向或垂直方向，这是Laplacian与soble的区别。下面这张图可以很好的表征出二者的区别：来源于OpenCV官方文档 

卷积的一些作用还参考了网上的一些解释，罗列如下：

（1）

（2）

一种是滤波，比如最简单的高斯模板，就是把模板内像素乘以不同的权值然后加起来作为模板的中心像素值，如果模板取值全为1，就是滑动平均；如果模板取值为高斯，就是加权滑动平均，权重是中间高，四周低，在频率上理解就是低通滤波器；如果模板取值为一些边缘检测的模板，结果就是模板左边的像素减右边的像素，或者右边的减左边的，得到的就是图像梯度，方向不同代表不同方向的边缘；

另一种理解是投影，因为当前模板内部图像和模板的相乘累加操作就是图像局部patch和模板的内积操作，如果把patch和模板拉直，拉直的向量看成是向量空间中的向量，那么这个过程就是patch向模板方向上的投影，一幅图像和一个模板卷积，得到的结果就是图像各个patch在这个方向上的response map或者feature map；如果这样的模板有一组，我们可以把这一组看成一组基，得到的一组feature map就是原图像在这组基上的投影。常见的如用一组Garbor滤波器提取图像的特征，以及卷积神经网络中的第一层，图像在各个卷积核上的投影。