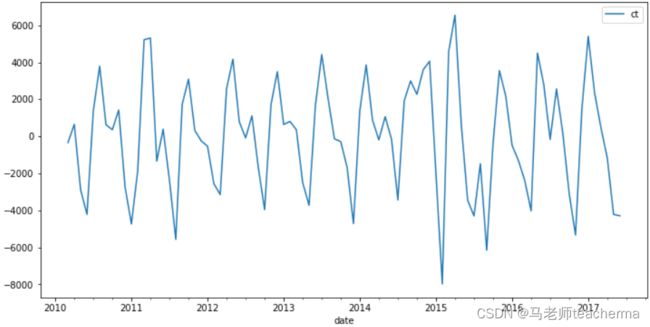
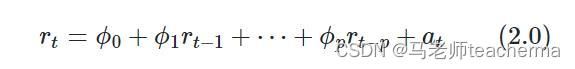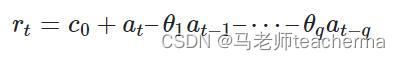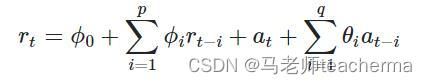时间序列预测

**

1.时间序列构成要素

**
长期趋势，季节变动，循环变动，不规则变动。
影响时间序列不稳定主要有趋势和季节性两个因素。
**

2.平稳性的判断标准

**
均值（与t无关）、方差（与t无关）、协方差（只与时间间隔有关）。

3.平稳性分类

3.1 严平稳
(rt1,rt2,…,rtk)的联合分布在时间的平移变换下保持不变，这是个很强的条件。
3.2 宽平稳
rt与rt−l的协方差不随时间而改变，l为任意整数。
**

4.平稳性检测方法

**
4.1 单位根检验
检验序列中是否存在单位根，利用ADF测试自回归模型是否存在单位根，ADF检验测试结果由测试统计量和一些置信区间的临界值组成。如果“测试统计量”少于“临界值”，我们可以拒绝无效假设，并认为序列是稳定的。

from statsmodels.tsa.stattools import adfuller

def test_stationarity(timeseries, window=12):
    rolmean = timeseries.rolling(window=window, center=False).mean()
    rolstd = timeseries.rolling(window=window, center=False).std()
    orig = plt.plot(timeseries, color='blue', label='Original')# 设置原始图，移动平均图和标准差图的式样
    mean = plt.plot(rolmean, color='red', label='Rolling Mean')
    std = plt.plot(rolstd, color='black', label='Rolling Std')
    plt.legend(loc='best')  # 使用自动最佳的图例显示位置
    plt.title('Rolling Mean & Standard Deviation')
    plt.show() #供肉眼观察是否平稳
    print('ADF检验结果：')
    dftest = adfuller(timeseries, autolag='AIC')  # 使用减小AIC的办法估算ADF测试所需的滞后数
    # 将ADF测试结果、显著性概率、所用的滞后数和所用的观测数打印出来
    dfoutput = pd.Series(dftest[0:4], index=['Test Statistic', 'p-value', 'Num Lags Used', 'Num Observations Used'])
    for key, value in dftest[4].items():
        dfoutput['Critical Value (%s)' % key] = value
    print(dfoutput)
test_stationarity(ts_week)

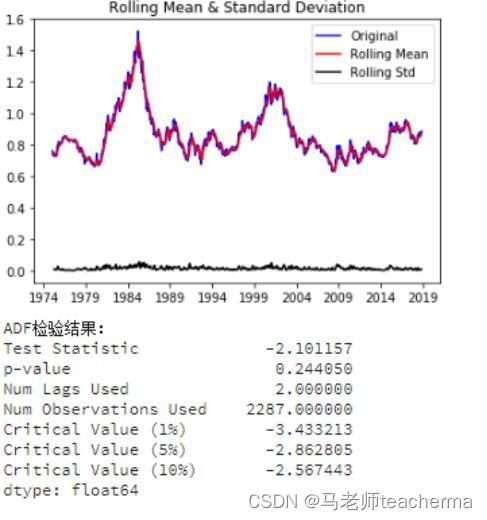
Test Statistic的值如果比Critical Value (5%)小则满足稳定性需求。
p-value越低（理论上需要低于0.5）证明序列越稳定。
4.2 白噪声检验
对于纯随机序列，即白噪声序列，各项数值没有关系，序列完全随机波动，可以终止对该序列的分析，白噪声序列没有信息可提取。
#生成一个伪随机白噪声用于测试acorr_ljungbox的可靠性

from statsmodels.stats.diagnostic import acorr_ljungbox  #导入白噪声检验函数
from random import gauss

whitenoise = pd.Series([gauss(0.0, 1.0) for i in range(1000)]) #创建一个高斯分布的白噪声
print(u'白噪声检验结果为：', acorr_ljungbox(whitenoise,lags=1)) #检验结果：平稳度，p-value。p-value>0.05为白噪声

**

5.时间序列转换为平稳序列

**
5.1 检测稳定性（利用上面方法）
5.2 消除趋势
取对数，平方根、立方根。
移动平均数：根据序列频率采用K连续值的平均数。
加权移动平均：权重被指定给先前的值连同衰减系数。进行消除操作后，继续检验稳定性，直到选取合适的消除趋势算法为止。

#取对数
ts_log = np.log(ts)
plt.plot(ts_log)

#移动平均数
moving_avg = ts_log.rolling(12).mean()
plt.plot(ts_log)
plt.plot(moving_avg, color='red')
ts_log_moving_avg_diff = ts_log - moving_avg
ts_log_moving_avg_diff.head(12)
test_stationarity(ts_log_moving_avg_diff)

#加权移动平均
expwighted_avg = ts_log.ewm(halflife=12).mean()
plt.plot(ts_log)
plt.plot(expwighted_avg, color='red')
ts_log_ewma_diff = ts_log - expwighted_avg
test_stationarity(ts_log_ewma_diff)

5.3 消除季节性
差分：采用一个特定时间差的差值。

ts_log_diff = ts_log.diff() # ts_log_diff = ts_log - ts_log.shift()
plt.plot(ts_log_diff)
ts_log_diff.dropna(inplace=True)
test_stationarity(ts_log_diff)

分解：将时间序列数据分解为趋势、季节性、残差三部分。

from statsmodels.tsa.seasonal import seasonal_decompose
decomposition = seasonal_decompose(ts_log)

trend = decomposition.trend
seasonal = decomposition.seasonal
residual = decomposition.resid

plt.subplot(411)
plt.plot(ts_log, label='Original')
plt.legend(loc='best')
plt.subplot(412)
plt.plot(trend, label='Trend')
plt.legend(loc='best')
plt.subplot(413)
plt.plot(seasonal,label='Seasonality')
plt.legend(loc='best')
plt.subplot(414)
plt.plot(residual, label='Residuals')
plt.legend(loc='best')
plt.tight_layout()
#计算残差稳定性
ts_log_decompose = residual
ts_log_decompose.dropna(inplace=True)
test_stationarity(ts_log_decompose)

**

6.时间序列建模

**
6.1 自相关系数 ACF
相关系数度量了两向量相关性，而在平稳时间序列中，想知道rt与rt-i的相关性，称rt与rt-l的相关系数为rt的间隔为l的自相关系数。

对一个平稳的时间序列样本rt，间隔为l的自相关系数的估计为，则函数ρ^1,ρ2,ρ^3…称为rt的样本自相关函数(ACF)。

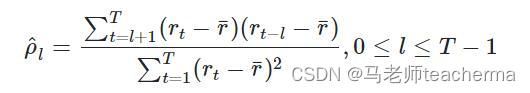
6.2 自相关图
偏自相关函数（PACF）用来度量暂时调整所有其他较短滞后的项后，时间序列以K个时间单位分隔之间的相关。

import statsmodels.api as sm
sm.graphics.tsa.plot_acf(data, lags=50)
plt.figure(figsize=(12, 6))
plt.show()
#PACF
sm.graphics.tsa.plot_pacf(data, lags=50)
plt.figure(figsize=(12, 6))
plt.show()

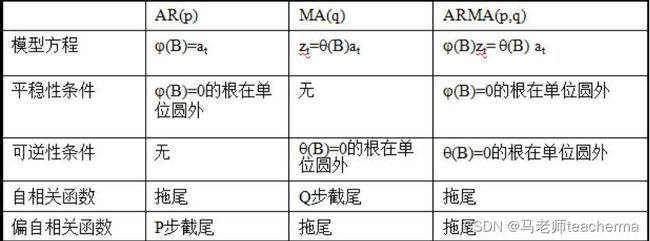
截尾指ACF或PACF在某阶后均为0的性质，即大于K后快速趋于0。
拖尾指ACF或PACF并不在某阶后均为0，即不会在某个数后为0。
6.3 白噪声与线性序列
两随机变量的协方差为0，称为纯随机过程，对于这个过程来说，若期望和方差均为常数，则称为白噪声过程。
很多序列具有线性性，如AR,MA,ARMA都是线性模型。
6.4 自回归模型 AR

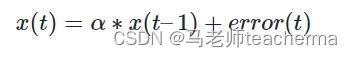
这个方程为AR公式，表示下一个点完全依赖前面一个点，AR具有惯性特性：

AR§模型如下：

需要检验模型平稳性以及计算特征根。

change_data = data['change_pct'] # 载入收益率序列
change_data = np.array(change_data, dtype=np.float)
model = sm.tsa.AR(change_data)
results_AR = model.fit()
plt.figure(figsize=(12,6))
plt.plot(change_data, 'b', label = 'changepct')
plt.plot(results_AR.fittedvalues, 'r', label = 'AR model')
plt.legend()
print(len(results_AR.roots)) # 模型阶数
#画出特征根检验平稳性
r1 = 1
theta = np.linspace(0, 2*np.pi, 360)
x1 = r1 * np.cos(theta)
y1 = r1 * np.sin(theta)
plt.figure(figsize=(6,6))
plt.plot(x1, y1, 'k')  # 画单位圆
roots = 1 / results_AR.roots  # 计算results_AR.roots后取倒数
for i in range(len(roots)):
    plt.plot(roots[i].real, roots[i].imag, '.r', markersize=8)  #画特征根
plt.show()

所有点（特征根）都在单位圆内，则序列平稳。
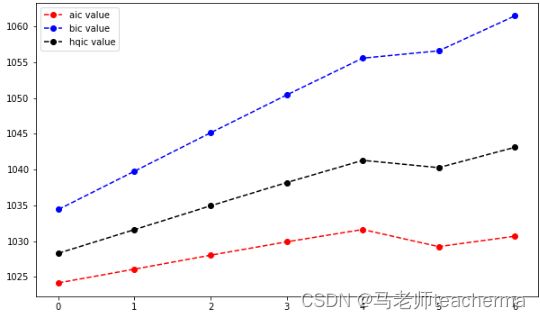
AR模型阶数的确定有两种方法：PACF和信息准则函数（AIC,BIC,HQIC），AIC即赤池信息量，BIC即贝叶斯信息量，HQIC即汉南-奎因信息量，公式如下：

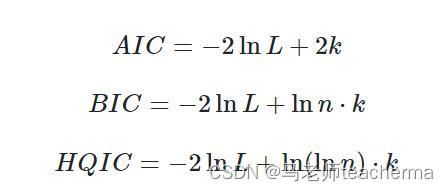
#PACF
fig = plt.figure(figsize=(12,6))
ax1 = fig.add_subplot(111)
fig = sm.graphics.tsa.plot_pacf(change_data, lags=40, ax=ax1)

#信息准则  优先考虑AIC最小的
aicList = []
bicList = []
hqicList = []
for i in range(1,8):  #从1阶开始算
    order = (i,0)  # 使用ARMA模型，其中MA阶数为0，只考虑了AR阶数。
    chgdataModel = sm.tsa.ARMA(change_data,order).fit()
    aicList.append(chgdataModel.aic)
    bicList.append(chgdataModel.bic)
    hqicList.append(chgdataModel.hqic)

plt.figure(figsize=(10,6))
plt.plot(aicList,'ro--',label='aic value')
plt.plot(bicList,'bo--',label='bic value')
plt.plot(hqicList,'ko--',label='hqic value')
plt.legend(loc=0)

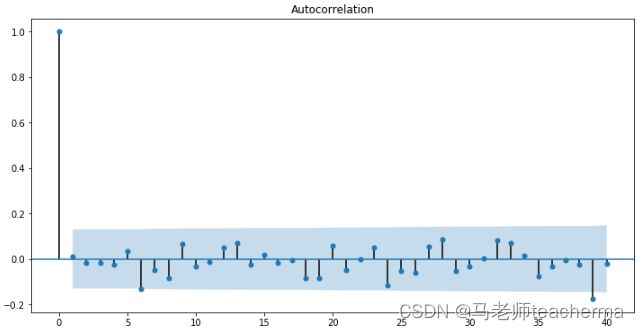
对于建立完成的AR模型需进行检验，若模型充分，则其残差序列应为白噪声。

#求出残差序列
delta = results_AR.fittedvalues - change_data[15:] # 取得误差项
plt.figure(figsize=(10,6))
# plt.plot(change_data[17:],label='original value')
# plt.plot(results_AR.fittedvalues,label='fitted value')
plt.plot(delta,'r',label=' residual error')
plt.legend(loc=0)

#检验是否白噪声
acf,q,p = sm.tsa.acf(delta,nlags=10,qstat=True)  # 计算自相关系数 及p-value
out = np.c_[range(1,11), acf[1:], q, p]
output=pd.DataFrame(out, columns=['lag', "ACF", "Q", "P-value"])
output = output.set_index('lag')
print(output)

6.5 滑动平均 MA
MA(q)模型中，噪声冲击会随着时间迅速消失，AR模型对冲击有持久的作用。

模型：

该模型使用了过去q时刻的随机干扰来线性表达当前预测。MA模型总是弱平稳，对于q阶的MA模型，其ACF总是q步截尾，用ACF进行定阶。

fig2 = plt.figure(figsize=(12,6))
ax2 = fig2.add_subplot(111)
fig2 = sm.graphics.tsa.plot_acf(change_data,lags=40,ax=ax2)

6.6 自回归-滑动平均 ARMA
AR和MA之间主要区别是基于不同时间点的时间序列对象相关性，ARMA将两个结合一起，使用的参数个数很小，如下：

该方程所有解的倒数称为该模型的特征根，如果所有的特征根的模都小于1，则该ARMA模型是平稳的。有一点很关键：ARMA模型的应用对象应该为平稳序列！下面的步骤都是建立在假设原序列平稳的条件下的。

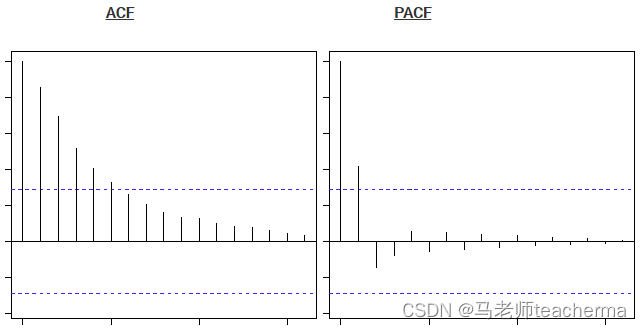
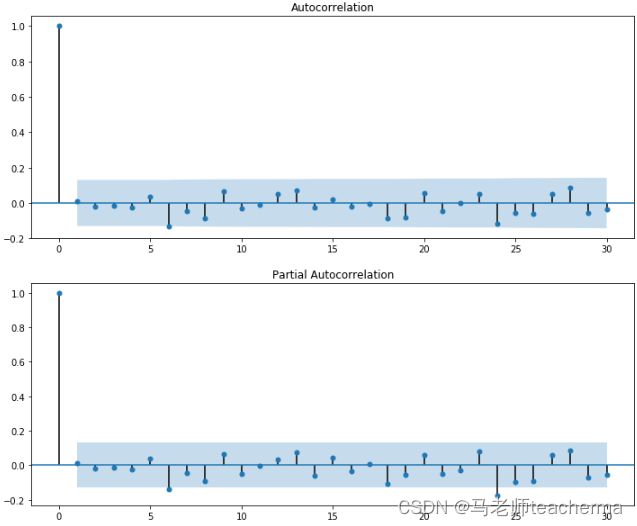
上图在第二滞后之后在PACF 曲线上有一个截止，这意味着这主要是AR过程。

上图在第二滞后之后在ACF 曲线上有一个截止，这意味着这主要是MA过程。
分别观察ACF和PACF来判断p和q的值。

fig = plt.figure(figsize=(12,12))
ax1=fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(change_data,lags=30,ax=ax1)
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(change_data,lags=30,ax=ax2)

根据模型的形式、特性以及自相关、偏相关等，特征总结如下：

6.7 差分自回归滑动平均模型 ARIMA
如果序列不是平稳的，可以使用ARIMA模型，I代表差分。一个非平稳序列结果d次差分可以转化为平稳时间序列，d的具体取值需要对差分后的序列进行平稳性检验，如果非平稳，则继续差分，直到平稳为止。其主要有三个参数p，q，d。

首先，一阶差分

diff1 = data.diff(1)
diff1.plot(figsize=(12,6))

二阶差分

diff2 = data.diff(2)
diff2.plot(figsize=(12,6))

这样d设置为1或2即可，基本是平稳序列，确定q和p的方法同ARMA类似，信息准则+ACF+PACF综合确定，取AIC,BIC,HQIC最小值。
6.8 SARIMAX
ARIMA用于单变量时间序列数据预测的。该方法可以处理具有趋势的数据，但不支持具有季节性组件的时间序列。支持对该系列季节性组成部分进行直接建模的ARIMA扩展称SARIMA。它增加了三个新的参数来指定系列季节性成分的自回归（AR），差分（I）和移动平均（MA），以及季节性周期的附加参数。
趋势参数：
p：趋势自回归阶数
d：趋势差分阶数
q：趋势移动平均阶数
季节性参数：
P：季节性自回归阶数
D：季节性差分阶数
Q：季节性移动平均阶数
m：单个季节期间的时间步数