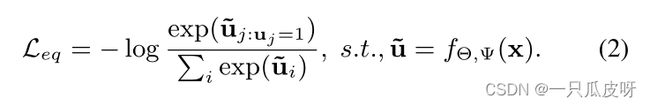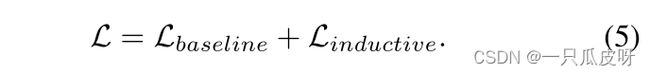Exploring Complementary Strengths of Invariant and Equivariant Representations for Few-Shot Learning
论文信息
基本信息：CVPR-2021
论文地址：https://openaccess.thecvf.com/content/CVPR2021/papers/Rizve_Exploring_Complementary_Strengths_of_Invariant_and_Equivariant_Representations_for_Few-Shot_CVPR_2021_paper.pdf
https://openaccess.thecvf.com/content/CVPR2021/papers/Rizve_Exploring_Complementary_Strengths_of_Invariant_and_Equivariant_Representations_for_Few-Shot_CVPR_2021_paper.pdf
代码地址：
GitHub - nayeemrizve/invariance-equivariance: "Exploring Complementary Strengths of Invariant and Equivariant Representations for Few-Shot Learning" by Mamshad Nayeem Rizve, Salman Khan, Fahad Shahbaz Khan, Mubarak Shah (CVPR 2021)"Exploring Complementary Strengths of Invariant and Equivariant Representations for Few-Shot Learning" by Mamshad Nayeem Rizve, Salman Khan, Fahad Shahbaz Khan, Mubarak Shah (CVPR 2021) - GitHub - nayeemrizve/invariance-equivariance: "Exploring Complementary Strengths of Invariant and Equivariant Representations for Few-Shot Learning" by Mamshad Nayeem Rizve, Salman Khan, Fahad Shahbaz Khan, Mubarak Shah (CVPR 2021)
https://github.com/nayeemrizve/invariance-equivariance
Abstract
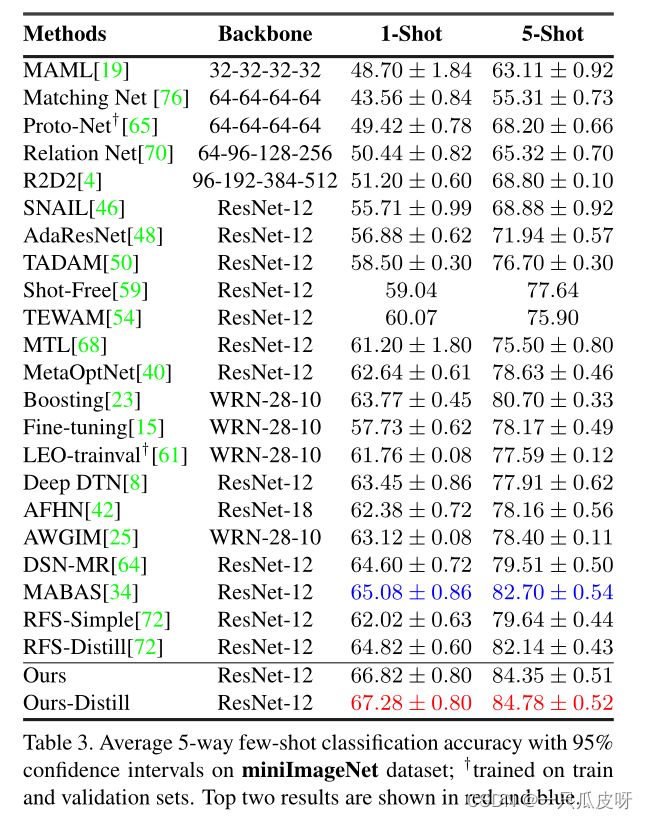
在许多现实世界的问题中，收集大量标记样本是不可行的。少样本学习 (FSL) 是解决此问题的主要方法，其目标是在存在有限数量的样本的情况下快速适应新类别。 FSL 任务主要是通过利用基于梯度的元学习和度量学习方法的思想来解决的。然而，最近的工作已经证明了强大的特征表示与简单的嵌入网络的重要性，它可以胜过现有的复杂 FSL 算法。在这项工作中，我们建立在这种洞察力的基础上，并提出了一种新颖的训练机制，该机制同时对一组通用的几何变换实施等变性和不变性。等变性或不变性已在以前的工作中中单独使用；然而，据我们所知，它们并未被联合使用。对这两个对比目标的同时优化 允许模型共同学习 不仅独立于输入变换而且编码几何变换结构的特征的特征。这些互补的特征集有助于很好地推广到只有少数数据样本的新类。我们通过结合一个新的自我监督蒸馏目标实现了额外的改进。我们广泛的实验表明，即使没有知识蒸馏，我们提出的方法也可以在五个流行的基准数据集上优于当前最先进的 FSL 方法。
Introduction
FSL 主要是使用元学习的思想来解决的。两种最主要的方法是基于优化的元学习 [19, 32, 61] 和基于度量学习的方法 [65, 70, 1]。两组方法都试图训练一个基础学习器，该基础学习器可以在存在一些新的类示例时快速适应。然而，最近在 [55] 中表明，基础学习器的快速适应关键取决于特征重用。最近的其他工作 [72, 15, 10] 也表明，在所有元训练集上训练的基线特征提取器可以达到与最先进的基于元学习的方法相当的性能。这带来了一个有趣的问题：通过简单地改进基本特征提取器，FSL 性能可以提高多少？
为了回答这个问题，首先，我们来看看机器学习 (ML) 算法中的归纳偏差。所有 ML 算法的优化利用不同的归纳偏差进行假设选择；因为解决方案从来都不是唯一的。这些算法的泛化通常依赖于归纳偏差的有效设计，因为它们编码了我们对一组特定解决方案的先验偏好。例如，像 ℓ1/ℓ2-penalties [73]、dropout [66] 或提前停止 [52] 等正则化方法通过选择更简单的解决方案在优化过程中隐含地强加奥卡姆剃刀。同样，卷积神经网络 (CNN) 通过设计强加了平移不变性 [2]，这使得内部嵌入平移等变。受此启发，几种方法 [12, 20, 16] 试图通过对不同的几何变换施加等变性来泛化 CNN，从而可以更有效地对数据的内部结构进行建模。另一方面，像[37]这样的方法试图通过学习变换不变特征来对抗讨厌的变化。然而，这种归纳偏差并不能提供对 FSL 任务的最佳泛化，并且 FSL 的有效归纳设计的设计相对来说还没有被探索。
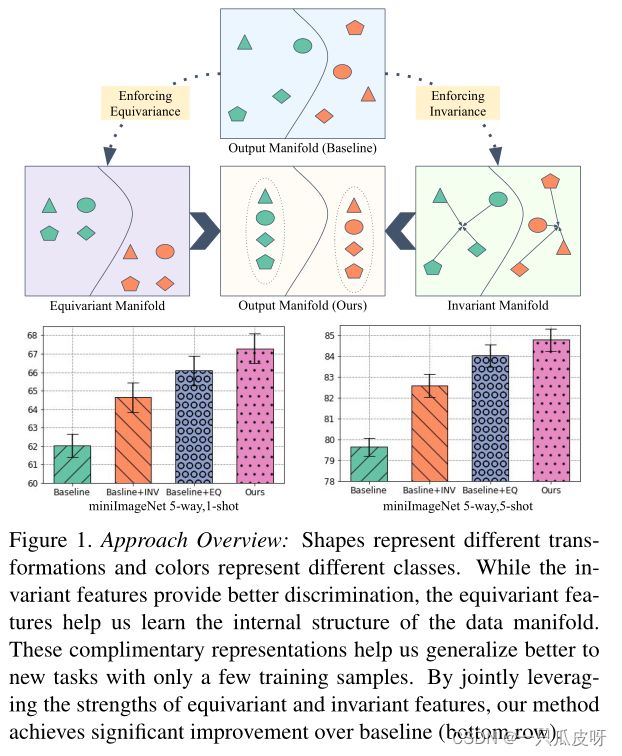
在本文中，我们通过设计一组有效的归纳偏差提出了一种新颖的特征学习方法。我们观察到实现输入变换不变性所需的特征可以提供更好的区分，但不能确保最佳泛化。类似地，专注于转换判别的特征对于类判别不是最优的，而是学习有助于学习数据结构的等变属性，从而获得更好的可迁移性。因此，我们建议通过同时寻求保留不变和等变特征的多任务目标来结合两种特征类型的互补优势。我们认为学习这样的通用特征会鼓励基础特征提取器更通用。我们通过对多个基准数据集进行广泛的实验来验证这一说法。我们还进行了彻底的消融研究，以证明同时执行等方差和不变性优于单独执行这些目标中的任何一个（见图 1）。
Contributions
- 我们对一组通用的几何变换实施互补等变性和不变性，以对数据的底层结构进行建模，同时保持区分性，从而提高 FSL 的泛化能力。
- 我们没有进行广泛的架构更改，而是通过将自我监督任务定义为辅助监督来提出一个简单的替代方案。对于等变性，我们引入了一个变换判别任务，同时开发了一个实例判别任务来学习变换不变特征。
- 我们通过保留方差属性的跨任务知识蒸馏展示了额外的收益。
Method
1. 问题定义
少样本学习 (FSL) 分两个阶段进行，首先训练一组基类上的模型，然后在推理时接收一组新的小样本类。
为了解决 FSL 任务，大多数元学习方法都利用了情景训练方案。一个eposde由一个小的训练和测试集(,)组成。一个eposide的训练集和测试集的示例是从相同的分布中采样的，即来自元训练类的相同子集。元学习方法试图通过解决这些eposide的集合来优化基础学习器的参数。主要动机是评估条件应该在基础训练阶段进行模拟。然而，根据最近的工作，我们不使用情景训练方案，该方案允许我们训练单个可推广模型，该模型可以有效地用于任意方式、任意shot设置而无需重新训练。具体来说，我们以监督的方式在整个基础训练集 Db 上训练我们的基础学习器。
假设我们的 FSL 任务的基础学习器是一个神经网络 fΘ，参数化为参数Θ。这个基础学习器的作用是提取可以泛化新类的良好特征嵌入。基础学习器 fΘ 可以将输入图像 x 投影到嵌入空间 fΘ : x→ z 中，使得 z∈ 。现在，为了优化基础学习器 fΘ 的参数，我们需要一个分类器将提取的嵌入投影到标签空间中。为此，我们引入了一个分类函数 fΦ，其参数Φ 将嵌入 z 投影到标签空间 Y 中，即 fΦ : z→~y，使得~y∈ Y。
我们通过最小化整个基础训练集 Db 上的交叉熵损失来联合优化 fΘ 和 fΦ 的参数。分类损失由下式给出:
为了规范两个子网络的参数，我们添加了一个正则化项。因此，我们的基线训练算法的学习目标变为：
2. 通过自监督学习注入归纳偏差
我们建议通过简单地执行自我监督学习 (SSL) 来对一组通用几何变换 T 实施等变性和不变性。自我监督对于在不访问语义标签的情况下学习一般特征特别有用。对于表示学习，自监督方法通常旨在实现某些输入转换的等变性，或者通过使表示不变来学习区分实例。据我们所知，在自监督文献中尚未探索到一组通用几何变换 T 的同时等变性和不变性。我们是第一个这样做的人。
变换集 T 可以从几何变换族 DT 中获得； T～DT。在这里，DT 可以解释为一系列几何变换，如欧几里得变换、相似变换、仿射变换和投影变换。所有这些几何变换都可以用具有不同自由度的 33 矩阵来表示。然而，对几何变换的连续空间 T 实施等方差和不变性是困难的，甚至可能导致次优解。为了克服这个问题，在这项工作中，我们量化了仿射变换的完整空间。我们通过将 DT 划分为 M 个离散的变换集来近似 DT。在这里，可以根据数据的性质和计算预算来选择 M。
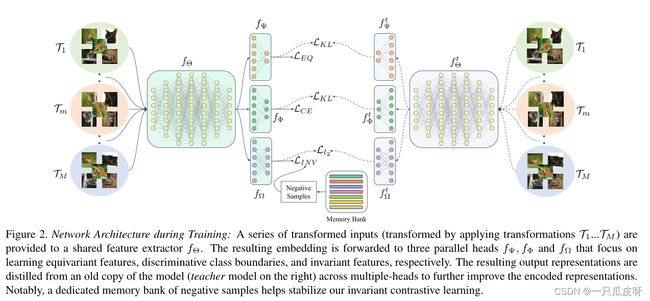
对于训练，我们通过应用所有 M 个变换来生成输入图像 x 的 M 个变换副本。然后我们将所有这些转换后的图像组合成一个张量， = {x0, x1, ..., xM-1}。这里，xi 是经过第 i 次变换的输入图像 x，Ti（为了清楚起见，在后面的讨论中去掉了 xi 的下标）。我们将此复合输入发送到网络并针对等变性和不变性进行优化。训练以多任务方式进行。除了基线监督训练所需的分类头之外，还在基础学习器之上添加了另外两个头，如图 2 所示。这些头中的一个用于强制等变性，另一个用于强制不变性。这种多任务训练方案确保基础学习器在输出嵌入中保留变换等变和不变特征。我们在下面解释了我们的感应损耗的每个组成部分。
2.1 增强等变性
如上所述，等变特征有助于我们对数据的固有结构进行编码，从而提高特征对新任务的泛化能力。为了对包含 M 个量化变换的集合 T 实施等变性，我们引入了一个带有参数 的 MLP 。的作用是将基学习器 z 的输出嵌入投影到等变空间中，即 : z→~，其中~∈ U⊂ 
。
为了训练网络，我们在没有任何人工监督的情况下创建代理标签。对于特定的变换，使用 M 维 one-hot 编码向量 u∈
（使得
）来表示的标签。一旦分配了代理标签，就会以有监督的方式使用交叉熵损失进行训练，如下所示：
这种在等变空间 U 中使用代理标签的监督训练可确保输出嵌入 z 保留变换等变特征。
2.2 增强不变性
虽然等变表示对于编码数据中的结构很重要，但它们对于类别区分可能不是最佳的。这是因为我们考虑的变换是不改变图像类别的变化，因此一个好的特征提取器还应该编码独立于这些输入变化的表示。为了对由 M 个量化变换组成的集合 T 实施不变性，我们引入了另一个带有参数 Ω 的 MLP Ω。 Ω的作用是将基学习器 z 的输出嵌入投影到不变空间中，即Ω : z→ v 其中 v∈ V⊂ ,D 是不变嵌入的维度。
为了优化不变性，我们利用对比损失 [26] 来进行实例区分。我们通过最大化对应于变换图像的嵌入 （经过第 m 个变换 Tm 之后）和参考嵌入 0（从原始图像嵌入而不应用任何变换 T）之间的相似性来强制不变性。重要的是，我们注意到在批次中选择负样例是不足够的去获得判别表示 [78, 47]。我们在对比损失中使用了一个内存库来采样更多的负样本，而不会任意增加批量大小。此外，存储库允许稳定的收敛行为[47]。我们的学习目标如下：
其中，m 表示变换索引，
表示内存中保存的参考 
的先前副本，函数 h(·) 定义为：
这里，s(.) 是相似函数，τ是温度，Dn 是从特定小批量的存储库中抽取的负样本集。请注意，我们还最大化了参考嵌入 与其过去的表示 之间的相似性，这有助于稳定学习。
2.3 多头蒸馏
一旦我们的模型学习了不变和等变表示，我们就使用自蒸馏来训练一个新模型，使用之前模型的输出作为锚点（图 2）。请注意，在典型的知识蒸馏 [31] 中，通过匹配其软化输出，信息从较大的模型（教师）交换到较小的模型（学生）。相比之下，相同模型的输出在自蒸馏 [21] 中匹配，其中平滑预测编码标签间依赖关系，从而帮助模型学习更好的表示。
在我们的案例中，通过配对 logits [72] 进行简单的知识蒸馏并不能确保先前模型版本学习的不变和等变表示的转移。因此，我们扩展了基于 logit 的知识蒸馏的想法，并将其应用于我们的不变和等变嵌入嵌入。具体来说，在最小化监督分类器头 fΦ 的软输出的 Kullback Leibler (KL) 散度的同时，我们还最小化了等变头 fΨ 的输出之间的 KL 散度。由于我们的不变头 fΩ 的输出不是概率分布，因此我们最小化了 L2 损失以提取该头的知识。知识蒸馏的总体学习目标如下：
2.4 总体目标
最后，我们通过结合等变 Leq、不变 Lin 和多头蒸馏 Lkd 损失来获得注入所需归纳偏差的结果损失：
总体损失只是归纳目标和基线目标的组合，
3. 小样本评估
为了评估，我们通过从包含新类图像的保留测试集中采样 FSL 任务来测试我们的基础学习器 。每个 FSL 任务包含一个支持集和一个对应的查询集 {Dsupp, Dquery}；两者都包含来自同一测试类子集的图像。使用 ，我们获得了 Dsupp 和 Dquery 图像的嵌入。在 [72] 之后，我们基于图像嵌入和来自 Dsupp 的相应标签训练了一个简单的逻辑回归分类器。我们使用该线性分类器来推断查询嵌入的标签。
实验
