python实现李航第十章HMM算法的前向、后向、维特比算法
python实现李航第十章HMM算法的前向、后向、维特比算法
- 前向算法
- 后向算法
- 维特比算法
前向算法
理论部分参考链接:前向算法
问题:给出 λ \lambda λ,求 P ( O ∣ λ ) P(O|\lambda) P(O∣λ)


以下只给结论,不给具体推导:
首先假设一个 α \alpha α
α t ( i ) = P ( o 1 . . . , o t , i t = q i ∣ λ ) \alpha{_t}{(i)}=P(o{_1}...,o{_t},i{_t}=q{_i}|\lambda) αt(i)=P(o1...,ot,it=qi∣λ)
α T ( i ) = P ( O , i T = q i ∣ λ ) \alpha{_T}{(i)}=P(O,i{_T}=q{_i}|\lambda) αT(i)=P(O,iT=qi∣λ)
P ( O ∣ λ ) = ∑ i = 1 N P ( O , i T = q i ∣ λ ) = ∑ i = 1 N α T ( i ) P(O|\lambda)=\sum{_{i=1}^N}P(O,i{_T}=q{_i}|\lambda)\\ \qquad \quad \ \ =\sum{_{i=1}^N}\alpha{_T}{(i)} P(O∣λ)=∑i=1NP(O,iT=qi∣λ) =∑i=1NαT(i)
α t + 1 ( i ) = ∑ j = 1 N b j ( O t + 1 ) ⋅ a i j ⋅ α t ( i ) \alpha{_{t+1}}{(i)}=\sum{_{j=1}^N}{b{_j}(O{_{t+1}}}){\cdot}a{_{ij}}\cdot{\alpha{_{t}}{(i)}} αt+1(i)=∑j=1Nbj(Ot+1)⋅aij⋅αt(i)
class HMM:
def forward(self,Q,V,A,B,O,PI):
"""
前向算法
Q:状态序列
V:观测集合
A:状态转移概率矩阵
B:生成概率矩阵
O:观测序列
PI:状态概率向量
"""
#序列的长度
T=len(O)
#观测变量有多少个状态
N=len(Q)
# alphas是前向概率矩阵,每列是某个时刻每个状态的前向概率
#alphas(t,i)=P(o1..ot,it=qi|miu)
alphas = np.zeros((T,N))
for t in range(T):
# 当前时刻观测值对应的索引
index_O = V.index(O[t])
for i in range(N):
if t == 0:
alphas[t][i] = PI[i] * B[i][index_O]
else:
# 这里使用点积和使用矩阵相乘后再sum没区别
alphas[t][i] = np.dot(alphas[t-1],[a[i] for a in A]) * B[i][index_O]
# 将前向概率的最后一行的概率相加就是观测序列生成的概率
#P(o|miu)=alpha(T,i) i=1,2..N
P = np.sum(alphas[T-1])
print('alphas :')
print(alphas)
print('P=%5f' % P)
if __name__ == '__main__':
Q = [1,2,3]
V = ['红', '白']
A = [[0.5, 0.2, 0.3], [0.3, 0.5, 0.2], [0.2, 0.3, 0.5]]
B = [[0.5, 0.5], [0.4, 0.6], [0.7, 0.3]]
# O = ['红', '白', '红', '红', '白', '红', '白', '白']
O = ['红', '白', '红','白'] #习题10.1的例子
PI = [0.2, 0.4, 0.4]
Hmm = HMM()
Hmm.forward(Q, V, A, B, O, PI)
输出为:
alphas :
[[0.1 0.16 0.28 ]
[0.077 0.1104 0.0606 ]
[0.04187 0.035512 0.052836 ]
[0.0210779 0.02518848 0.01382442]]
P=0.060091
后向算法
理论部分参考链接:前向算法
问题:给出 λ \lambda λ,求 P ( O ∣ λ ) P(O|\lambda) P(O∣λ)

以下只给结论,不给具体推导:
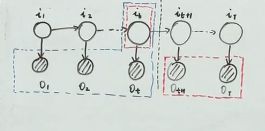
首先假设一个 β \beta β
β t ( i ) = P ( o t + 1 . . . , o T ∣ i t = q i , λ ) \beta{_t}{(i)}=P(o{_{t+1}}...,o{_T}|i{_t}=q{_i},\lambda) βt(i)=P(ot+1...,oT∣it=qi,λ)
…
β 1 ( i ) = P ( o 1 . . . , o T ∣ i 1 = q i , λ ) \beta{_1}{(i)}=P(o{_{1}}...,o{_T}|i{_1}=q{_i},\lambda) β1(i)=P(o1...,oT∣i1=qi,λ)
P ( O ∣ λ ) = ∑ i = 1 N P ( o 1 ∣ i 1 = q i ) ⋅ β 1 ( i ) ⋅ π i = ∑ i = 1 N b i ( o 1 ) ⋅ π i ⋅ β 1 ( i ) P(O|\lambda)=\sum{_{i=1}^N}P(o_1|i{_1}=q{_i})\cdot{}\beta_1(i)\cdot{\pi_i}\\ \qquad \quad \ \ =\sum{_{i=1}^N}b_i(o_1)\cdot{\pi_i}\cdot{}\beta_1(i) P(O∣λ)=∑i=1NP(o1∣i1=qi)⋅β1(i)⋅πi =∑i=1Nbi(o1)⋅πi⋅β1(i)
β t ( i ) = ∑ j = 1 N b j ( O t + 1 ) ⋅ a i j ⋅ β t + 1 ( j ) \beta{_{t}}{(i)}=\sum{_{j=1}^N}{b{_j}(O{_{t+1}}}){\cdot}a{_{ij}}\cdot{\beta{_{t+1}}{(j)}} βt(i)=∑j=1Nbj(Ot+1)⋅aij⋅βt+1(j)
import numpy as np
class HMM:
def backward(self, Q, V, A, B, O, PI):
"""
前向算法
Q:状态序列
V:观测集合
A:状态转移概率矩阵
B:生成概率矩阵
O:观测序列
PI:状态概率向量
"""
#序列的长度
T=len(O)
#观测变量有多少个状态
N=len(Q)
# betas是后向概率矩阵,每列是某个时刻每个状态的后向概率
# betas(t,i)=P(ot+1..oT|it=qi,miu)
betas = np.zeros((T,N))
for i in range(N):
betas[T-1][i] = 1
# 倒着,从后往前递推
for t in range(T-2,-1,-1):
for i in range(N):
for j in range(N):
betas[t][i] += A[i][j] * B[j][V.index(O[t+1])] * betas[t+1][j]
index_O = V.index(O[0])
P = np.dot(np.multiply(PI,[b[index_O] for b in B]),betas[0])
print("P(O|lambda)=", end="")
for i in range(N):
print("%.1f*%.1f*%.5f+" % (PI[i], B[i][index_O], betas[0][i]), end="")
print("0=%f" % P)
print(betas)
if __name__ == '__main__':
Q = [1,2,3]
V = ['红', '白']
A = [[0.5, 0.2, 0.3], [0.3, 0.5, 0.2], [0.2, 0.3, 0.5]]
B = [[0.5, 0.5], [0.4, 0.6], [0.7, 0.3]]
# O = ['红', '白', '红', '红', '白', '红', '白', '白']
O = ['红', '白', '红','白'] #习题10.1的例子
PI = [0.2, 0.4, 0.4]
Hmm = HMM()
Hmm.backward(Q, V, A, B, O, PI)
输出:
P(O|lambda)=0.2*0.5*0.11246+0.4*0.4*0.12174+0.4*0.7*0.10488+0=0.060091
[[0.112462 0.121737 0.104881]
[0.2461 0.2312 0.2577 ]
[0.46 0.51 0.43 ]
[1. 1. 1. ]]
维特比算法
理论部分参考链接:前向算法
问题:给出 λ \lambda λ,求 P ( O ∣ λ ) P(O|\lambda) P(O∣λ)


以下只给结论,不给具体推导:
首先假设一个 δ \delta δ,用来记录状态序列1-t的值最大为多少
δ t ( i ) = max i 1 . . . . i t − 1 P ( o 1 . . . , o t , i 1 . . . i t − 1 , i t = q i ) \delta{_t}{(i)}=\max \limits_{i{_1}....i{_{t-1}}}P(o{_{1}}...,o{_t},i{_1}...i{_{t-1}},i{_t}=q{_i}) δt(i)=i1....it−1maxP(o1...,ot,i1...it−1,it=qi)
…
δ t + 1 ( i ) = max 1 ≤ i ≤ N δ t ( i ) a i j b j ( o t + 1 ) \delta{_{t+1}}{(i)}=\max \limits_{1\leq i\leq N}\delta{_t}{(i)}a{_{ij}}b{_j}(o{_{t+1}}) δt+1(i)=1≤i≤Nmaxδt(i)aijbj(ot+1)
在假设一个 ψ \psi ψ,用于记录上一个观测状态的状态
ψ t + 1 ( j ) = arg max 1 ≤ i ≤ N δ t ( i ) ⋅ a i j \psi{_{t+1}}(j)=\arg\max\limits_{1\leq i\leq N}\delta{_t}{(i)}\cdot{a_{ij}} ψt+1(j)=arg1≤i≤Nmaxδt(i)⋅aij
import numpy as np
class HMM:
def viterbi(self,Q,V,A,B,O,PI):
N = len(Q)
T = len(O)
# deltas是记录每个时刻,每个状态的最优路径的概率
deltas = np.zeros((T,N))
# psis是记录每个时刻每个状态的前一个时刻的概率最大的路径的节点(psia的记录是比deltas晚一个时刻的)
psis = np.zeros((T,N))
# I是记录最优路径的
I = np.zeros(T)
for t in range(T):
index_O = V.index(O[t])
for i in range(N):
if t == 0 :
deltas[t][i] = PI[i] * B[i][index_O]
psis[t][i] = 0
else:
deltas[t][i] = np.max(np.multiply(deltas[t-1],[a[i] for a in A])) * B[i][index_O]
psis[t][i] = np.argmax(np.multiply(deltas[t-1],[a[i] for a in A]))
# 直接取最后一列最大概率对应的状态为最优路径最后的节点
I[T-1] = np.argmax(deltas[T-1])
for t in range(T-2,-1,-1):
# psis要晚一个时间步,起始将最后那个状态对应在psis那行直接取出就是最后的结果
# 但是那样体现不出回溯,下面这种每次取上一个最优路径点对应的上一个最优路径点
I[t] = psis[t+1][[int(I[t+1])]]
print(I)
if __name__ == '__main__':
Q = [1,2,3]
V = ['红', '白']
A = [[0.5, 0.2, 0.3], [0.3, 0.5, 0.2], [0.2, 0.3, 0.5]]
B = [[0.5, 0.5], [0.4, 0.6], [0.7, 0.3]]
# O = ['红', '白', '红', '红', '白', '红', '白', '白']
O = ['红', '白', '红','白'] #习题10.1的例子
PI = [0.2, 0.4, 0.4]
Hmm = HMM()
Hmm.viterbi(Q, V, A, B, O, PI)
输出:
[2. 1. 1. 1.]