pytorch(六)—— 感知机
pytorch 感知机
- Perception 感知机
- torch实现perception
- Ref:
Perception 感知机
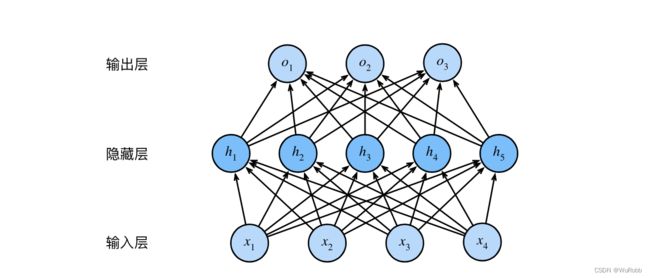
一个简单的网络图为下图所示:
4个输入单元,3个输出单元
如果用 X \pmb X XXX表示输入, O \pmb O OOO表示输出, H \pmb H HHH表示隐藏层。
H = X ⋅ w 1 + b 1 O = H ⋅ w 2 + b 2 \pmb H = \pmb X · \pmb w _1+ \pmb b_1 \\\pmb O = \pmb H · \pmb w _2+ \pmb b_2 HHH=XXX⋅www1+bbb1OOO=HHH⋅www2+bbb2
在大多数情况下,线性模型不能很好的拟合模型,这时候将Hidden layer的拟合关系变成曲线,就可以很好的适合不同的场景,这个曲线Function叫做Activation Function。
Activation Function 具体可以参考上篇文章。
如果加入sigmoid function激活,输出层就变成了
O = σ ( H ⋅ w 2 + b 2 ) \pmb O = \sigma(\pmb H · \pmb w _2+ \pmb b_2 ) OOO=σ(HHH⋅www2+bbb2)
torch实现perception
数据集采用fashion_mnist,稍微定义一个比较复杂的网络,输入层为784, 输出为10,hidden layer一层有256个,采用ReLU函数激活,这样的话网络的式子为
H = X ⋅ w 1 + b 1 O = R e L U ( H ⋅ w 2 + b 2 ) \pmb H = \pmb X · \pmb w _1+ \pmb b_1 \\\pmb O = R eLU(\pmb H · \pmb w _2+ \pmb b_2 ) HHH=XXX⋅www1+bbb1OOO=ReLU(HHH⋅www2+bbb2)
w 1 w_1 w1的shape为 ( 784 , 256 ) (784,256) (784,256), b 1 b_1 b1的shape为 ( 256 , ) (256,) (256,);
w 2 w_2 w2的shape为 ( 256 , 10 ) (256, 10) (256,10), b 2 b_2 b2的shape为 ( 10 , ) (10,) (10,)。
import torch
import matplotlib.pyplot as plt
from torch import nn
from d2l import torch as d2l
# 载入数据集
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
# weight
num_inputs, num_outputs, num_hiddens = 784, 10, 256
W1 = nn.Parameter(
torch.randn(num_inputs, num_hiddens, requires_grad=True) * 0.01
)
b1 = nn.Parameter(
torch.zeros(num_hiddens, requires_grad=True)
)
W2 = nn.Parameter(
torch.randn(num_hiddens, num_outputs, requires_grad=True) * 0.01
)
b2 = nn.Parameter(
torch.zeros(num_outputs, requires_grad=True) * 0.01
)
params = [W1, b1, W2, b2]
编写网络结构
net = nn.Sequential(
nn.Flatten(),
nn.Linear(784, 256), # 隐藏层线性模型
nn.ReLU(), # 激活隐藏层
nn.Linear(256, 10)
)
带有一层hidden layer的perception就构建好了,接下来就可以带入利用torch自动求导进行训练。
def acc(X,y,net):
p_predict = net(X)
y_predict = torch.argmax(p_predict,axis=1)
output = y_predict - y
right_pre = len(output[output==0])
right_accu = right_pre/len(output)
return right_accu
loss = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(net.parameters(), lr=0.01)
epochs = 20
train_accu_history = []
test_accu_history = []
train_loss = []
for epoch in range(epochs):
for X,y in train_iter:
l = loss(net(X), y)
optimizer.zero_grad()
l.backward()
optimizer.step()
l = loss(net(X), y)
train_loss.append(l.detach())
train_batch = 0
train_accu = 0
test_batch = 0
test_accu = 0
for X_train,y_train in train_iter:
train_accu += acc(X_train, y_train, net)
train_batch += 1
train_avg_acc = train_accu/train_batch
train_accu_history.append(train_avg_acc)
for X_test,y_test in test_iter:
test_accu += acc(X_test, y_test, net)
test_batch += 1
avg_acc = test_accu/test_batch
test_accu_history.append(avg_acc)
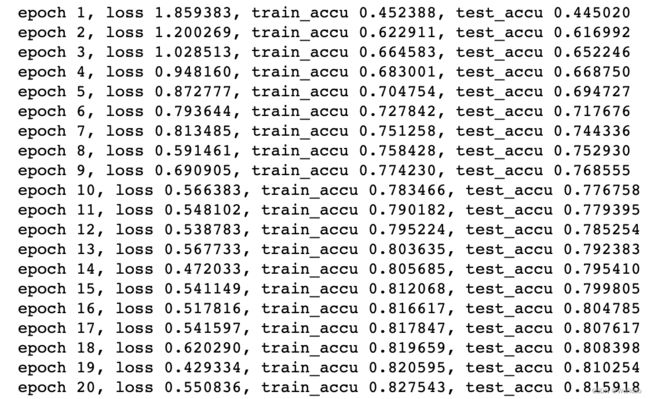
print(f'epoch {epoch + 1}, loss {l:f}, train_accu {train_avg_acc:f}, test_accu {avg_acc:f}')
Ref:
[1] 阿斯顿·张 李沐等,《动手学深度学习》,北京:人民邮电出版社,2019
[2] 李航,《统计学习方法(第2版)》, 北京:清华大学出版社,2019