控原笔记(1)——Matlab建立控制系统模型
控原笔记(1)——Matlab建立控制系统模型
-
- 介绍
- 传递函数的输入及零、极点计算
- 计算闭环传递函数与结构图的等效变换
介绍
无论是经典控制理论还是现代控制理论,控制系统的分析和设计方法都是以数学模型为基础进行的。Matlab可以分析用微分方程或传递函数形式描述的系统。可以使用Matlab输入系统的传递函数模型;计算函数的零、极点;计算闭环传递函数;完成结构图的等效变换等。
参考书籍:《自动控制原理》— 化学工业出版社(历玉鸣等主编)
传递函数的输入及零、极点计算
通常系统传递函数的表达有多种形式,如式:
G ( s ) = 4 s 2 − 12 s + 8 s 3 + 6 s 2 + 11 s + 6 = 4 ( s − 1 ) ( s − 2 ) ( s 2 + 3 s + 2 ) ( s + 3 ) = 4 ( s − 1 ) ( s − 2 ) ( s + 1 ) ( s + 2 ) ( s + 3 ) G(s) = \frac{4s^2-12s+8}{s^3+6s^2+11s+6} = \frac{4(s-1)(s-2)}{(s^2+3s+2)(s+3)} = \frac{4(s-1)(s-2)}{(s+1)(s+2)(s+3)} G(s)=s3+6s2+11s+64s2−12s+8=(s2+3s+2)(s+3)4(s−1)(s−2)=(s+1)(s+2)(s+3)4(s−1)(s−2)
与之对应的,Matlab也有各种不同传递函数的表示方法,常见的有直接用分子/分母表示,或者是用零极点及增益表示,对于上式中采用分子/分母系数方法,Matlab中具体输入如下:
>> num = [4 -12 8]; den = [1 6 11 6];
>> sys = tf(num, den)
输出分子/分母形式的传递函数:
sys =
4 s^2 - 12 s + 8
----------------------
s^3 + 6 s^2 + 11 s + 6
Continuous-time transfer function.
如果传递函数的分子或分母写成多项式乘积的形式,那么分子和分母也可以采用多项式乘法函数 conv() 来表示:
>> num = conv([4 -4],[1 -2]); den = conv([1 3 2],[1 3]);
对于上式中也可以采用零、极点及其增益的方法表示:
>> z = [1;2]; p = [-1; -2; -3]; k = 4;
>> sys = zpk(z, p, k)
输出零、极点及其增益形式的传递函数:
sys =
4 (s-1) (s-2)
-----------------
(s+1) (s+2) (s+3)
Continuous-time zero/pole/gain model.
以上两种模型之间可以相互转化,如:
>> [z, p, k] = tf2zp (num, den)
>> [num, den] = zp2tf (z, p, k)
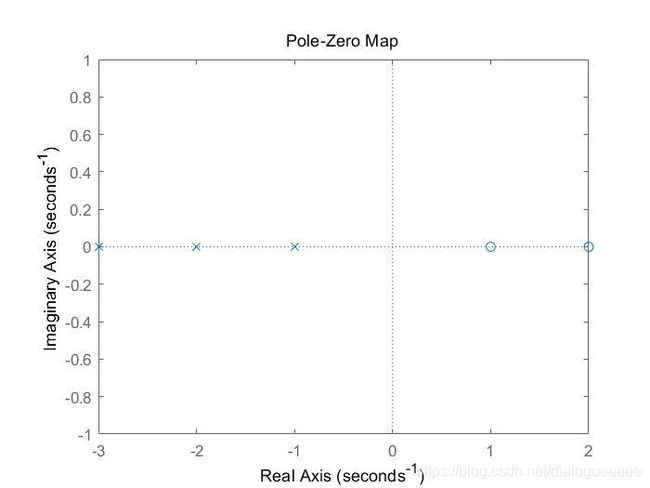
如果期望获得传递函数在零、极点内函数分布图,可以采用如下命令:
>> pzmap(sys)
计算闭环传递函数与结构图的等效变换
假设已经为某系统的各个环节建立了相应的传递函数的表达,接下来可以利用Matlab将各个环节联系起来,构成闭环控制系统,通过结构图的变换计算出从输入端到输出端的传递函数。
(1)串联
假设一简单的开环控制系统,由两个环节 G 1 ( s ) G_1(s) G1(s)和 G 2 ( s ) G_2(s) G2(s)串联而成,如图所示:

其中两环节的传递函数分别是:
G 1 ( s ) = s + 1 ( s + 2 ) ( s + 3 ) , G 2 ( s ) = 4 s ( s + 5 ) G_1(s)=\frac{s+1}{(s+2)(s+3)}, G_2(s)=\frac{4}{s(s+5)} G1(s)=(s+2)(s+3)s+1,G2(s)=s(s+5)4
那么可用串联函数series()求出该开环传递系统的传递函数:
>> num1 = [1 1]; den1 = conv([1 2], [1 3]); sys1 = tf(num1, den1);
>> num2 = [4]; den2 = [1 5 0]; sys2 = tf(num2, den2);
>> sys = series(sys1, sys2)
显示结果如下:
sys =
4 s + 4
----------------------------
s^4 + 10 s^3 + 31 s^2 + 30 s
Continuous-time transfer function.
(2)并联
若一简单开环控制系统,由上述两个环节 G 1 ( s ) G_1(s) G1(s)和 G 2 ( s ) G_2(s) G2(s)并联而成,如图所示:
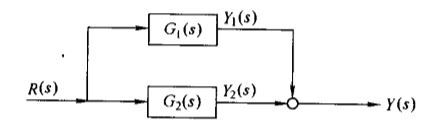
那么使用并联函数parallel()求出该开环控制系统的传递函数:
>> sys=parallel(sys1, sys)
显示结果如下:
sys =
s^3 + 10 s^2 + 25 s + 24
----------------------------
s^4 + 10 s^3 + 31 s^2 + 30 s
Continuous-time transfer function.
(3)反馈连接
若反馈控制系统由上述两个环节 G 1 ( s ) G_1(s) G1(s)和 G 2 ( s ) G_2(s) G2(s)构成,如图所示:
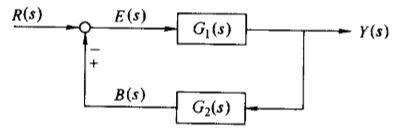
那么使用反馈连接函数feedback()可以求出其闭环传递系统的传递函数:
>> sys = feedback(sys1, sys2, -1)
其中"-1"表示负反馈连接,为缺省设置。如果两环节是正反馈连接,可以使用"1"来表示。上述Matlab语句显示结果如下:
sys =
s^3 + 6 s^2 + 5 s
--------------------------------
s^4 + 10 s^3 + 31 s^2 + 34 s + 4
Continuous-time transfer function.
如果环节 G 2 ( s ) G_2(s) G2(s)的传递函数为1,即构成单位反馈系统,可使用cloop()函数求解:
>> sys = cloop(sys1, -1)
显示结果如下:
sys =
s + 1
-------------
s^2 + 5 s + 6
Continuous-time transfer function.
了解上述三种系统连接函数之后,就可以利用他们实现结构图的变换。