神经常微分方程(NODE)介绍
NODE
Neural Ordinary differential equation是对ResNet或者RNN模块的一种连续化结果,二者每个block的计算公式如下:
h t + 1 = h t + f ( h t , θ t , t ) h_{t+1}=h_t+f(h_t,\theta_t,t) ht+1=ht+f(ht,θt,t)
对其进行适当的变换1可以得到:
h t + 1 = f ( h t , θ t , t ) + h t = Δ t Δ t f ( h t , θ t , t ) + h t = Δ t f ( h t , θ t , t ) Δ t + h t \begin{aligned} h_{t+1}&=f(h_t,\theta_t,t)+h_t\\ &=\frac{\Delta_t}{\Delta_t}f(h_t,\theta_t,t)+h_t\\ &=\Delta_t\frac{f(h_t,\theta_t,t)}{\Delta_t}+h_t \end{aligned} ht+1=f(ht,θt,t)+ht=ΔtΔtf(ht,θt,t)+ht=ΔtΔtf(ht,θt,t)+ht
这个式子实际上就是差分的计算公式(或者说是欧拉方法的离散形式)2,如果在此处忽略掉分母处的 Δ t \Delta_t Δt,则 f ( h t , θ t ) f(h_t,\theta_t) f(ht,θt)就可认为是在计算当前时刻系统的导数,而 h t h_t ht则为每个时刻系统的输出值。那么RNN就可认为是在求解一个时序系统 f ( h t , θ t ) f(h_t,\theta_t) f(ht,θt),该系统每隔 Δ t \Delta_t Δt时间输出一个值。实际应用中我们想要模拟的系统可能是在连续时刻输出值,或者是非等间隔时间输出.此时这样离散的求解形式就不再适用,可将block层数不断堆叠,采样间隔逐渐减小,转化成常微分方程的形式进行求解:
d h t + 1 d t = f ( h t , θ t , t ) \frac{dh_{t+1}}{dt}=f(h_t,\theta_t,t) dtdht+1=f(ht,θt,t)
从而给定初始状态 h t 0 h_{t0} ht0的情况下,我们可以利用网络得到任意时刻的系统输出:
h ( t ) = h ( t 0 ) + ∫ t 0 t f ( h ( u ) , θ ( u ) , u ) d u h(t)=h(t_0)+\int_{t_0}^{t}f(h(u),\theta(u),u)du h(t)=h(t0)+∫t0tf(h(u),θ(u),u)du
当 f f f为用神经网络模拟的系统时,这就是一个NODE。其中 θ ( u ) \theta(u) θ(u)是网络的参数(实际上此时并不随着时刻变化,因为不再分为多个block, θ ( u ) = θ \theta(u)=\theta θ(u)=θ), h ( t ) h(t) h(t)为网络在 t t t时刻的输出, h ( t 0 ) h(t_0) h(t0)为系统的初始状态。而这一积分虽然没有解析解,但目前已经有许多工具可以对其进行近似求解,因此无需关注具体求解细节,我们可以得到系统任意时刻的输出为:
O D E s o l v e r ( h ( t 0 ) , f , t 0 , t 1 , θ t ) ODEsolver(h(t_0),f,t_0,t_1,\theta_t) ODEsolver(h(t0),f,t0,t1,θt)
前向传播的问题解决了来看反向传播,为了优化网络的参数需要求取损失函数对 θ t \theta_t θt的导数。因此需要计算损失函数对求解器的导数,再计算求解器输出对于 θ t \theta_t θt的导数,如果直接使用链式求导法则求梯度来反向传播,就意味着我们只能使用可微的求解器。同时这些求解器都往往以迭代的形式工作的(类似于ResNet每个block),前向传播过程中需要保存每一次的结果用于反向传播的计算。如果要求系统模拟的精度非常高,迭代次数就会很多,需要保存非常大的计算图,很浪费资源。因此反向传播过程采用了伴随灵敏度法,解决要保存前向传播时所有激活状态的弊端。3具体推导过程如2中所示,不再赘述。
总而言之,NODE用来在网络中代替Resblock模块,NODE就相当于多个Resblock的级联。假定输入为系统 t 0 t_0 t0时间点的状态,使用网络 f f f对真实系统的动态特性进行模拟,通过ODE求解这样一个系统在 t 1 t_1 t1时刻的状态(设置 [ t 0 , t 1 ] = [ 0 , 1 ] [t_0,t_1]=[0,1] [t0,t1]=[0,1]),利用反向传播来更新系统的参数。需要获得系统在多个时间点输出时,就假定输入为为系统 t 0 t_0 t0时间点的状态时,设置多个时间点 t 1 , t 2 . . . t N t_1,t_2...t_N t1,t2...tN,以同样的方式求解即可。
与ResNet相比,NODE的优势在于参数量少,耗费的计算资源少。这一点不难理解,因为NODE虽然可以认为是无限多个Resblock的连续化,但由于网络参数也不再随着时间点变化( θ ( t ) → θ \theta(t)\rightarrow\theta θ(t)→θ),因此参数量更少。而在实际运算过程中,虽然ODE同样是以迭代的形式如同ResNet一样前向计算,但使用了伴随灵敏度法反向传播的ODE不用在前向传播过程中保存状态,因此内存为 O ( 1 ) O(1) O(1)。此外,NODE方法对于准曲率和效率的追求是可控的,通过控制ODE solver的tolerance我们可以控制系统求解所需的时间。需要高精度时就使用较小的tolerance,反之亦然。
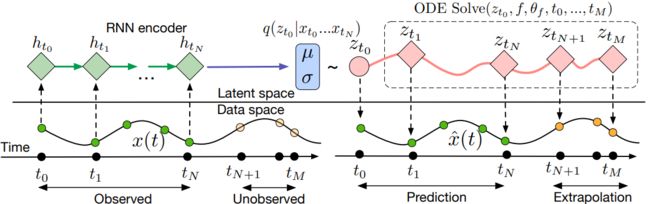
此外在具体应用层面,由于其输出时间点的连续性,我们可以用NODE对序列数据进行插值或者是预测。假定序列数据可以通过另一条隐状态组成的序列来表征,那么我们可以使用encoder来获得序列数据在初始时刻的隐状态 z 0 z_0 z0,再使用NODE来模拟后续观测时刻的隐状态 z 1 , z 2 , . . . , z N z_1,z_2,...,z_N z1,z2,...,zN,最后使用Decoder将隐状态序列重新映射回数据序列。以这样一种VAE的模式训练网络,我们就可以利用NODE获得任意时刻的隐状态,再通过decoder就能获得任意时刻的序列数据,无论是已知数据的插值还是未来数据的预测都可以完成。图示如下:
总结
NODE最令人称道的特性就是其输出的连续性,这使我们可以利用非等间隔采样的数据作为输入,同时可以获得任意时刻的预测输出。而相对的trick如伴随灵敏度法,ODEsolver则显得没有那么重要,当作完全黑盒处理即可。
参考
NEURAL NETWORKS AS ORDINARY DIFFERENTIAL EQUATIONS ↩︎
Understanding Neural ODE’s ↩︎ ↩︎
Understanding Adjoint Method of Neural ODE ↩︎