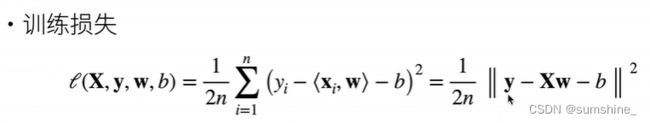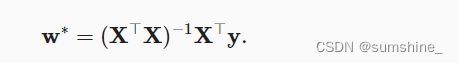【动手学习深度学习】3线性神经网络

目录

3.1. 线性回归——预测问题

3.1.1. 线性回归的基本元素

3.1.1.1. 线性模型 

3.1.1.2. 损失函数

3.1.1.3. 解析解

3.1.1.4. 随机梯度下降

3.1.2 线性回归的从0开始实现

3.1.3 线性回归的简洁实现

3.2 softmax回归——分类

3.2.1 softmax回归模型

3.2.2 softmax函数

3.2.3 交叉熵损失

3.2.4 softmax回归的实现

---

3.1. 线性回归——预测问题

线性回归的基本逻辑可以理解为：在已有数据上，将结果视为y，比如预测房屋价格，房屋价格就是y，将影响结果的原因设为X，X有可能有多个，如房屋的位置、大小、购买年份等都会影响房屋价格，这些变量可以组成一个向量X。对X输入进行加权(W)和偏移(b)得出y值公式，之后就可以对于X已知y未知的数据做出预测。

3.1.1. 线性回归的基本元素

3.1.1.1. 线性模型 

 线性模型可以看做是单层神经网络 

3.1.1.2. 损失函数

 绝对值损失函数：

L1和L2合并——鲁棒损失

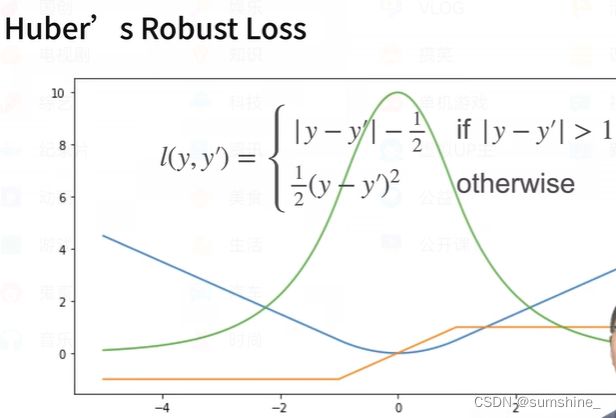蓝色是损失函数 黄色是损失函数导数 绿色是似然函数

对于线性回归模型： 

 

在训练模型时，我们希望寻找一组参数（w∗,b∗）， 这组参数能最小化在所有训练样本上的总损失。

3.1.1.3. 解析解

线性回归刚好是一个很简单的优化问题。 与在本书中所讲到的其他大部分模型不同，线性回归的解可以用一个公式简单地表达出来， 这类解叫作解析解（analytical solution）。

线性回归的解析解：

3.1.1.4. 随机梯度下降

——无法得到解析解的情况下，用梯度下降找最优解

小批量随机梯度下降（minibatch stochastic gradient descent）：在每次需要计算更新的时候随机抽取一小批样本

超参数（hyperparameter）：可以调整但不在训练过程中更新的参数

批量大小（batch size）：每个小批量中的样本数

批量大小和学习率的值通常是手动预先指定，而不是通过模型训练得到的。

3.1.2 线性回归的从0开始实现

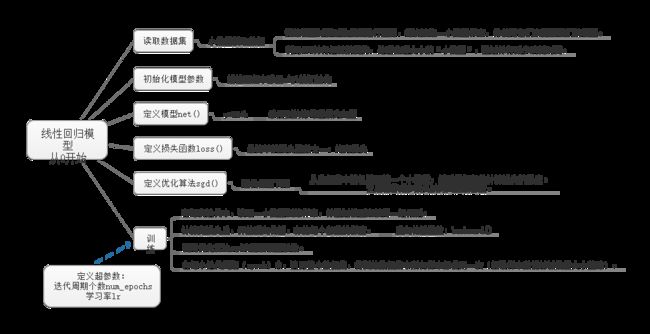线性回归模型从0开始思维导图

3.1.3 线性回归的简洁实现

线性回归模型简洁实现思维导图

与从头实现相比，简洁实现通过调用pytorch库里的类实现部分功能

3.2 softmax回归——分类

3.2.1 softmax回归模型

softmax回归也是一个单层神经网络，输出层也是全连接层。

softmax回归与线性回归的区别在于输出。线性回归输出为1，softmax的输出为多，所有的输出均受所有输入的影响。

举一个softmax的例子，假设每次输入是一个2×2的灰度图像。 用一个标量表示每个像素值，每个图像对应四个特征x1,x2,x3,x4。 此外，假设每个图像属于类别“猫”，“鸡”和“狗”中的一个。设o∈{1,2,3}， 其中整数分别代表{狗,猫,鸡}。需要注意的是：因为分类问题一般与类别之间的自然顺序无关，为了去除影响，会采用独热编码（one-hot encoding）。对这个例子进行one-hot编码：o将是一个三维向量， 其中(1,0,0)对应于“猫”、(0,1,0)对应于“鸡”、(0,0,1)对应于“狗”，o∈{(1,0,0),(0,1,0),(0,0,1)}。

3.2.2 softmax函数

在这个公式中，向量O代表类别，向量y代表不同类别的概率

 尽管softmax是一个非线性函数，但softmax回归的输出仍然由输入特征的仿射变换决定。 因此，softmax回归是一个线性模型（linear model）。

3.2.3 交叉熵损失

                                        ——分类问题最常用的损失之一

交叉熵损失函数公式

3.2.4 softmax回归的实现

在实现的步骤上与线性回归其实没有什么不同，只是具体的一些函数有所区别。

网络模型：

net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))

损失函数为：

loss = nn.CrossEntropyLoss(reduction='none')

注：线性回归和softmax回归实现的具体代码在本地中，其中还附上了讲解，这里就做一些简单记录，不赘述了。