排队论（Queuing Theory）
目录
简介
一、基本概念
1.1 排队过程的一般表示
1.2 排队系统的组成和特征
1.2.1 输入过程
1.2.2 排队规则
1.2.3 服务过程
1.3 排队模型的符号表示
1.4 排队系统的运行指标
二、 输入过程与服务时间的分布
2.1 泊松流与指数分布
2.2 常用的几种概率分布
2.2.1 连续型随机变量分布
2.2.2 离散型随机变量分布
三、 生灭过程
四、 M/M/s 等待制排队模型
4.1 但服务台模型
4.1.1 队长的分布
4.1.2 几个主要数量指标
4.1.3 忙期和闲期
4.3 多服务台模型（编辑）
十、 排队模型的计算机模拟
10.1 确定随机变量概率分布的常用方法
10.2 计算机模拟
简介
排队论起源于1909年丹麦电话工程师A.K.爱尔朗的工作，他对电话通过拥挤问题进行了研究。1917年，爱尔朗发表了他的著名文章——“自动电话交换中的概率论的几个问题的解决”。排队论已广泛应用于军事、运输、维修、生产、服务、库存、医疗卫生、教育、水利灌溉之类的问题，显示了强大的生命力。
排队是在日常生活中经常遇到的现象，如顾客到商店购买物品、病人到医院看病常需要排队。此时要求服务的数量超过服务机构（服务台，服务员等）的容量。也就是说，到达的顾客不能立即得到服务，因而出现了排队现象。这种现象不仅在个人日常生活中出现，电话局的占线问题，车站、码头等交通枢纽的车船堵塞喝疏导，故障机器的停机维修，水库的存贮调节等，都是有形或无形的排队现象。由于顾客到达喝服务时间的随机性。可以说排队现象几乎是不可避免的。
排队论也成为随机服务系统理论，就是为解决上述问题而发展的一门学科。它研究的内容有下列三部分：
- 性态问题，即研究各种排队系统的概率规律性，主要是研究队长分布、等待时间分布和忙期分布，包括了瞬态和稳态两种情形。
- 最优化问题，又分静态最优和动态最优，前者指最优设计，后者指现有排队系统的最优运营。
- 排队系统的统计推断，即判断一个给定的排队系统符合与哪种模型，以便根据排队理论进行分析研究。
这里将介绍排队论的一些基本知识，分析几个常见的排队模型。
一、基本概念
1.1 排队过程的一般表示
虚线包含的部分为排队系统。
凡要求服务的对象统称为顾客，为顾客服务的人或物称为服务员，由顾客和服务员组成服务系统。
服务机构过小，一直不能满足要求服务的顾客的需求；服务机构过大，相应消耗的财力和物力也增加。因此研究排队模型的目的就是要在顾客需要和服务机构的规模之间进行权衡决策，使其达到合理的平衡。
1.2 排队系统的组成和特征
一般的排队过程都由输入过程、排队规则、服务过程三部分组成。
1.2.1 输入过程
输入过程是指顾客到来实践的规律性，可能有以下几种情况：
- 顾客源是有限还是无限
- 顾客是逐个到达还是成批到达
- 顾客达到是相互独立还是相互影响
- 输入过程是平稳还是非平稳。平稳输入过程即顾客相继到达的时间间隔分布，及其数学期望、方差等数字特征都与时间无关。
1.2.2 排队规则
排队规则指到达排队系统的顾客按怎样的规则排队，可分为损失制，等待制和混合制三种。
- 损失制。当顾客到达时，所有的服务台均被占用，顾客离去。
- 等待制。当顾客到达时，所有的服务台均被占用，顾客排队等待知道接受完服务。
- 混合制。介于损失制和等待制两者之间。
1.2.3 服务过程
服务机构，单服务台；多服务台并联，多服务台串联；混合型。
服务规则：
- 先到先服务，FCFS
- 后到先服务，LCFS
- 随即服务，RAND
- 优先服务，PR
1.3 排队模型的符号表示
排队模型的一般表示方法，
- X代表顾客到达流或者顾客到达时间间隔的分布
-(Markov)指数分布
-确定型分布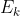
-k阶爱尔朗Erlang分布- G-一般服务时间分布
- GI-一般相互独立的时间间隔分布
- Y代表服务时间的分布
- 表示的字母所代表的分布与X相同
- Z代表服务台数目
- A代表系统容量限制
- B代表顾客源数目
- C代表服务规则
1.4 排队系统的运行指标
平均队长
：指系统内的顾客数（包括正在被服务以及正在排队的顾客）
平均排队长
：只指系统内正在排队的顾客数
平均逗留时间
：指顾客从进入排队系统到离开排队系统的时间，包括排队时间和被服务时间
平均等待时间
：指顾客排队的时间
平均忙期
：指顾客到达空闲机构起，到服务机构再次空闲的时间间隔长度的数学期望。
计算这些指标的基础是表达系统状态的概率，所谓系统的状态即指系统中顾客数。如果系统中有n个顾客就说系统的状态是n，它有如下几种表示方法及其代表含义：
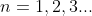队长没有限制。
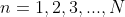，队长有限制，且最大数为N。
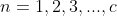，损失制且服务台个数为c时。
需注意排队系统的状态是时间t的函数，所以在时刻t、系统状态为n的概率用
表示。稳态，即与不随时间t改变时，系统状态记为
二、 输入过程与服务时间的分布
排队系统中的事件流包括顾客到达流和服务时间流，由于顾客到达的间隔时间和服务时间不可能是负值，因此分布是非负随机变量的分布。常用的分布有泊松分布，确定型分布，指数分布和爱尔朗分布。
2.1 泊松流与指数分布
输入过程是泊松流时，顾客相继到达的时间间隔T必服从指数分布。详细推到略去。
2.2 常用的几种概率分布
2.2.1 连续型随机变量分布
- 均匀分布
- 正态分布
- 指数分布
- Gamma分布
- Weibull分布
- Beta分布
2.2.2 离散型随机变量分布
- 均匀分布
- Bernoulli分布
- Poisson分布
- 二项分布
三、 生灭过程
一类非常重要且广泛存在的排队系统时生灭过程排队系统。生灭过程是一类特殊的随机过程，在生物学、物理学、运筹学中有广泛的应用。在排队论中，如果
表示在t时刻，系统中的顾客数，则
就构成了一个随机过程。如果用”生“代表示顾客的到来，”灭“表示顾客的离去。则对于许多排队过程来说，就是一类特殊的随机过程——生灭过程。
设为一个随机过程。若的概率分布具有以下性质：
- 假设
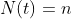，则从时刻t起到下一个顾客到达时刻止的时间服从参数为
的负指数分布，n=0,1,2... - 假设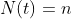，则从时刻t起到下一个顾客离去时刻止的时间服从参数为
的负指数分布，n=0,1,2,... - 同一时刻只有一个顾客到达或离去。
则称为生灭过程。
四、 M/M/s 等待制排队模型
4.1 但服务台模型
表示顾客相机到达时间服从参数为
的负指数分布，服务时间V服从参数为
的负指数分布，系统空间无限，允许无限排队，这是一类最简单的排队系统。
4.1.1 队长的分布
记
为系统达到平衡状态后队长的概率分布。记
，并设其小于1（否则队长无穷）。则队长分布为
数据量
是服务系统中至少有一个顾客的概率，也就是服务台处于忙的状态的概率，因而
也称为服务强度，反映了系统繁忙的程度。
4.1.2 几个主要数量指标
由于队长的概率分布已知，可以计算出该模型中的其他运行指标
平均队长
平均排队长
平均逗留时间
平均等待时间
显然有
，
4.1.3 忙期和闲期
平均忙期
平均闲期
4.3 多服务台模型（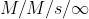
）
设顾客单个到达，相机达到时间间隔服从参数为的负指数分布，系统中有s个服务台，每个服务台的服务时间相互独立，且服从参数为的负指数分布。且为等待制，队长无限长，等待时间无限。
记
为系统达到平稳状态后，队长N的概率分布。
则队长的分布为
，其中![p_0=[\sum_{n=0}^{s-1}\frac{\rho^n}{n!}+\frac{\rho^s}{s!(1-\rho_s)}]^{-1}](http://img.e-com-net.com/image/info8/22529bb8b3114beb8946237a43eb1f25.gif)
，
，称为多服务台系统的服务强度。
对于多服务台系统，记
为在系统顾客达到系统时需要等待的概率。
平均排队长
平均队长
平均逗留时间
平均排队时间
十、 排队模型的计算机模拟
10.1 确定随机变量概率分布的常用方法
根据一般知识和经验，假定概率分布的形式，然后由实际数据估计分布的参数。
直接由大量的实际数据作直方图，得到经验分布，再通过假设检验，拟合分布函数。
确实先验知识以及实验数据时，对于区间
内变化的随机变量，可选用beta分布和均匀分布。现根据经验确定随机变量的均值和频率最高的数值
，则beta分布最终端参数
10.2 计算机模拟
当排队系统的到达间隔时间和服务时间的概率分布很复杂时，就需要使用随机模拟法求解。
随机模拟法要求事件能够按历史的概率分布规律出现。
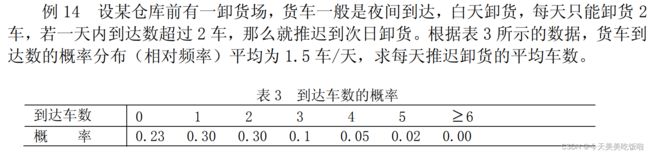
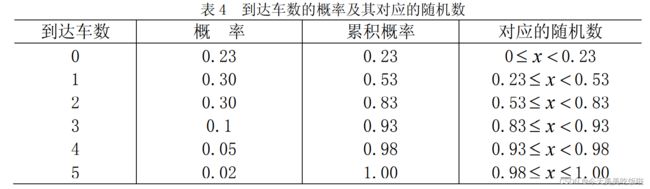
设a1表示生成的随机数，a2表示到达的车辆，a3表示需要卸货的车数，a4表示实际卸货车数，a5表示推迟卸货车数。
n=50000; %模拟50000天
m=2;
a1=rand(n,1);
%% 模拟实际达到的车数
a2=a1;
a2(find(a1<0.23))=0;
a2(find(a1>=0.2&&a1<0.53))=1;
a2(find(a1>=0.53&&a1<0.83))=2;
a2(find(a1>=0.83&&a1<0.93))=3;
a2(find(a1>=0.93&&a1<0.98))=4;
a2(find(a1>=0.98))=5;
%% 模拟卸货车数
a3=zeros(n,1);
a4=a3;
a5=a3;
a3(1)=a2(1);
if a3(1)<=m
a4(1)=a3(1);
a5(1)=0;
else
a4(1)=m;
a5(1)=a2(1)-m;
end
for i=2:n
a3(i)=a2(i)+a5(i-1);
if a3(i)<=m
a4(i)=a3(i);
a5(i)=0;
else
a4(i)=m;
a5(i)=a3(i)-m;
end
end
%%求平均
a=[a1 a2 a3 a4 a5];
sum(a)/n;