连续型数据处理
上一节,我们总结了离散型数据的处理方法,这一节我们整理下连续型数据的处理方法。一般来讲,离散型数据都是类别值,如:男生,女生,商务座,一等座,二等座等等。连续型数据基本上都是数值型数据,如年龄(10岁,11岁…),身高(110cm, 175cm…),海拔,薪资等等。
既然连续型数据都是数值,是可以直接拿来供计算机使用的,那么连续型数据该如何处理?这里我们提出一个处理思想:连续型数据离散化。连续型数据离散化以后的建模效果一定会比原来的好吗?这个答案是不一定的,任何时候我们都需要对两者结果进行比较,从而做出判断–连续型数据是否需要离散化?
连续型数据离散化的方法:对连续型数据进行分组处理。假如高三一班的学生身高从150cm~185cm,那么我们可以将身高数据划分为几组,如[150 ~ 160, 161 ~ 170,171 ~ 180,181 ~ 185],同时可以给每个组贴一个标签[稍矮,矮,高,非常高]。
接下来,我们将使用Pandas库来对具体的连续型数据进行分组处理。
数据集导入:
下载链接:链接:https://pan.baidu.com/s/1RhK-qrlLTOTv5FgQGEN1wQ
提取码:tga9
代码演示:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns;sns.set()
fcc = pd.read_csv('D:\\Py_dataset\\fcc_2016_coder_survey_subset.csv',encoding = 'utf-8')
fcc_df = fcc[['ID.x','Age','EmploymentField','Income']]#从原始数据集中,抽出几列供我们分析
#对数据集中的"Income"特征进行可视化展示
fig,ax = plt.subplots()
fcc_df['Income'].hist(color = 'blue')
ax.set_xlabel('Income')
ax.set_ylabel('quantity')
ax.set_title('The distribution of Income')
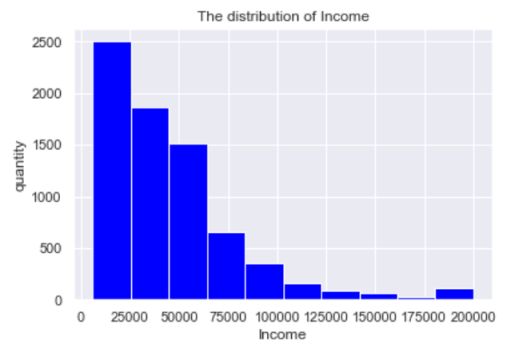
接下来我们使用两种方法对fcc_df数据集的"Income"特征进行分组。
1.pandas.cut
bins = [0,50000,100000,150000,200000]#设置组距
labels = ['low_income','middle_income','middel_high_income','high_income']#设置每组的标签
fcc_df['Income_bins'] = pd.cut(fcc_df['Income'],bins = bins,labels = labels)
fcc_df['Income_bins'].value_counts().plot(kind = 'bar')
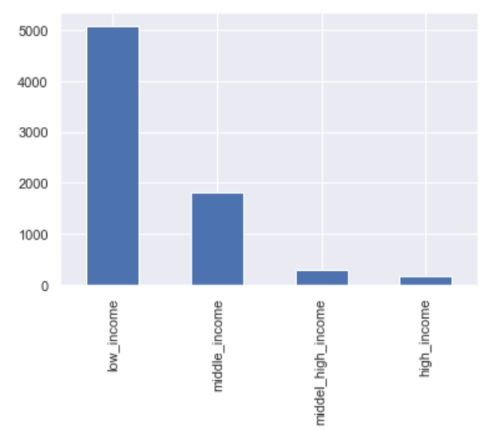
通过pandas.cut()方法,我们将连续的"Income"特征切分成了low_incoem,middle_income,middle_high_income,high_income四种类别。
2.Pandas.qcut()通过分位数切分
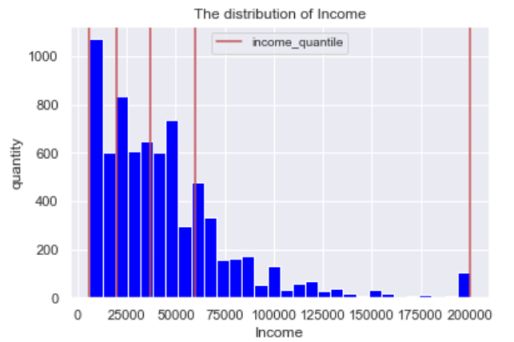
quantile_list = [0,0.25,0.5,0.75,1]#制定分位数
income_quantile = fcc_df['Income'].quantile(quantile_list)#将原始数据按照分位数进行切分
fig,ax = plt.subplots()
fcc_df['Income'].hist(color = 'blue',bins = 30)
for quantile in income_quantile:
qvl = plt.axvline(quantile,color = 'r')
ax.legend([qvl],['income_quantile'],fontsize = 10)
ax.set_xlabel('Income',fontsize = 12)
ax.set_ylabel('quantity',fontsize = 12)
ax.set_title('The distribution of Income',fontsize = 12)
quantile_labels = ['0~25%','25%~50%','50%~75%','75%~100%']
fcc_df['Income_range'] = pd.qcut(fcc_df['Income'],q = quantile_list)
fcc_df['Income_label'] = pd.qcut(fcc_df['Income'],q = quantile_list,labels = quantile_labels)
fcc_df.head()

总结:
本小节的连续数据离散化作为数据预处理的一种方式,目的是增加更多的数据特征。我们需要通过对比两者的建模效果,来做出判断 – 是否需要对连续数据进行离散化处理。