R语言--数据挖掘5---探索性聚类分析
探索性聚类分析
本次实验报告的内容为:
介绍数据。首先介绍数据的状况,数据大体代表的意思。
数据分为两个部分,一个是R语言自带的鸢尾花的数据;以及航空公司客户信息的数据air_data.csv
介绍原理。主要介绍两种聚类分析的方法,k-means聚类和层次聚类法。
案例分析。根据原来来对数据进行实际分析,对得到结果给出合理性的解释。
本次的案例分析分为两个部分,一部分是对iris数据的分析;另一部分是航空公司客户信息进行聚类分析;
总结。对当前做的事情做一个总结,自我评价一下不足。
参考及代码。
数据介绍
鸢尾花数据介绍:
本鸢尾花数据有五列数据,分别是Sepal.Length, Sepal.Width, petal.Length, petal.Width, Species。主要分为原始特征和花的类别,其中前四列代表鸢尾花的特征,分为两块,一个是鸢尾花花瓣,以及萼片,分别有长度和宽度两个特征,总共有四个特征;最后一列代表每个观测所代表的花的种类, 一共有150个观测数据。在本报告的分析中,我们主要是使用前面四列的特征来对鸢尾花的数据做聚类分析。
航空公司客户数据:
客户在某航空公司下的消费信息数据存储在air_data.csv,这些数据信息主要分为三块:客户基本信息、乘机信息和积分信息。本数据所包含的总特征有44个,总观测数有62988条记录。这些数据是根据末次飞行日期,选取宽度为两年的时间段作为分析观测窗口,从航空公司系统内抽取2012-04-01至2014-03-31内所有乘客的详细数据。在本次的分析报告中,我们首先对数据处理,从原始数据特征中抽取部分特征来进行聚类分析。
原理简介
关于聚类介绍的准备知识
数据标准化:分为中心标准化和最大最小值的标准化。在进行聚类之前,数据之间取值变量差异非常大,同时又存在单位不统一的情况,所以我们需要首先对原始数据进行标准化处理,再开始聚类。
我们主要是根据变量来对数据进行聚类,这里的变量分别有名义变量、定序变量、定距变量和定比变量。
名义变量的度量:名义变量取值是离散的,也就是说有有限个取值,这些取值中有些取值的所代表的重要性相差不大,有些相差就比较大。变量各个取值重要性相等的变量称为对称名义变量;重要性取值不等的成为非对称名义变量。
对于名义变量,他们之间的关系一般是用距离或者相似度来度量的。具体相似度度量参考课本114-115页。
**度量定序或定距变量:**对于定序变量的度量,一般是先转化为定距变量,再使用Minkoweski距离来度量的。当p=1时,是城市距离;当p=2时,是欧式距离;当 p = ∞ p = \infty p=∞时,是Chebyshev距离。
**度量定比变量:**1、使用定距变量的距离度量;2、使用另外三种对于非负定比的变量的,还有余弦相似度,以及相关系数的相似度来度量。其中余弦相似度一般用于文本挖掘中,对不同文本之间相似度的一个度量。
对于混合变量的度量:
一种方式:将名义变量转化为哑变量;定序变量转化为定距变量;再将所有的变量都转化为定距变量,使用度量定距变量的方法来度量。
另一种方式:遵从变量的原始类型,使用
s ( x , y ) = ∑ r = 1 p δ x , y r s x , y r ∑ r = 1 p δ x , y r s(\textbf{x}, \textbf{y}) = \cfrac{\sum_{r=1}^{p} \delta_{\textbf{x},\textbf{y}}^{r} s_{\textbf{x},\textbf{y}}^{r}}{\sum_{r=1}^{p} \delta_{\textbf{x},\textbf{y}}^{r}} s(x,y)=∑r=1pδx,yr∑r=1pδx,yrsx,yr
来度量。
其中
δ x , y r = { 1 对称名义,定序,定距,定比 非对称名义, x r , y r 同等重要 0 非同等重要 s x , y r = { 1 名义, x r = y r 0 名义, x r ≠ y r 1 − ∣ x r − y r ∣ R r 定序,定距,定比, R r 代表极差(全距) \delta_{\textbf{x},\textbf{y}}^{r} = \left\{ \begin{array}{ll} 1 & \textrm{对称名义,定序,定距,定比}\\ & \textrm{非对称名义,$x_r, y_r$同等重要} \\ 0 & \textrm{非同等重要} \end{array} \right. \\ s_{\textbf{x},\textbf{y}}^{r} = \left\{ \begin{array}{ll} 1 & \textrm{名义,$x_r=y_r$}\\ 0 & \textrm{名义,$x_r \ne y_r$} \\ 1-\cfrac{|x_r-y_r|}{R_r} & \textrm{定序,定距,定比, $R_r$代表极差(全距)} \end{array} \right. δx,yr=⎩⎨⎧10对称名义,定序,定距,定比非对称名义,xr,yr同等重要非同等重要sx,yr=⎩⎪⎪⎨⎪⎪⎧101−Rr∣xr−yr∣名义,xr=yr名义,xr=yr定序,定距,定比, Rr代表极差(全距)
相似性度量与距离度量的转换:一个事实:距离度量 d ( x , y ) d(x, y) d(x,y)总是能转化成相似性度量 s ( x , y ) s(x, y) s(x,y)。相似性度量在转化成正式的距离度量时,需要满足对称性,非负性以及当 x = y x=y x=y时, d ( x , y ) = 0 d(x, y)=0 d(x,y)=0,还有三角不等式性。且只有当相似度矩阵为非负定矩阵时,才能从相似度量中构造出满足上述四条性质的距离度量。
k-means聚类
k均值聚类步骤:
-
初始化K个聚类中心,可以随机选取。
-
固定中心,在每次循环中,将每个变量分到与其最近的中心。
C ( i ) = a r g min 1 ≤ l ≤ K d ( x i , v l ) , i = 1 , ⋯ , N C(i) = arg \min_{1 \le l \le K}d{(x_i, v_l)}, i=1, \cdots, N C(i)=arg1≤l≤Kmind(xi,vl),i=1,⋯,N -
固定每个变量的类,重新计算类的中心,在一个类中,找到一个点,使得它距离每个点的距离都很小。
v l = a r g min v ∑ i ∈ C i d ( x i , v ) , l = 1 , ⋯ , K v_l = arg \min_v \sum\limits_{i \in C_i}d(x_i, v), l=1, \cdots, K vl=argvmini∈Ci∑d(xi,v),l=1,⋯,K -
持续循环2和3, 直到所有类别中心的改变很小,或者达到实现规定的循环次数。
确定类别的个数:
使用伪F统计量来寻找最优的类别个数,其中伪F统计量定义为:
P s e u d o F = ( S S T − S S W ) / [ ( K − 1 ) p ] S S W / [ ( N − K ) p ] = ( S S T − S S W ) / ( K − 1 ) S S W / ( N − K ) \begin{aligned} Pseudo \quad F &= \cfrac{(SST - SSW)/[(K-1)p]}{SSW/[(N-K)p]} \\ & = \cfrac{(SST - SSW)/(K-1)}{SSW/(N-K)} \end{aligned} PseudoF=SSW/[(N−K)p](SST−SSW)/[(K−1)p]=SSW/(N−K)(SST−SSW)/(K−1)
其中SST代表总平方和,SSW代表组内平方和,SST-SSW代表组间平方和。伪F统计量的值越大,说明聚类结果的质量越高。
层次聚类法
画出聚类的坐标轴,横轴代表所聚的类,纵轴代表类别之间的距离。可以按照距离截断,就可以得到在截断距离画一条平行于X轴的水平线,就可以得到聚类的个数。
层次聚类的类型分为两种,合并式聚类法和分裂式层次聚类法。
其中,合并式聚类法:
(1)初始化时每个观测单独形成一个类别。
(2)迭代的将最相似(或距离最近)的两个类别合并。
(3)随着被合并的两个类别的相似度减小(或距离增加,因为相似度为1代表距离最小为0),最终所有观测都归于同一个类别。
分裂式层次聚类法:
(1)初始化所有观测都属同一个类别;
(2)迭代的将最不相似的两个子类别进行分裂。
(3)随着分裂成的两个子类别的相似度增加(或距离减小),最终每个观测单独形成一个类别。
对比两者:分列式层次聚类法的每一步都需要对比现有跟各个类别的各种分裂方式,算法复杂度高,因此一般使用合并式层次聚类法。
类别个数的确定:
这里是伪 t 2 t^2 t2统计量:
P s e u d o t 2 = [ S S W M − ( S S W l + S S W l ′ ) ] / p ( S S W l + S S W l ′ ) / [ ( N l + N l ′ − 2 ) ] p = S S W M − ( S S W l + S S W l ′ ) ( S S W l + S S W l ′ ) / ( N l + N l ′ − 2 ) \begin{aligned} Pseudo\quad t^2 & = \cfrac{[SSW_M-(SSW_l + SSW_{l'})]/p}{(SSW_l + SSW_{l'})/[(N_l + N_{l'}-2)]p} \\ &= \cfrac{SSW_M-(SSW_l + SSW_{l'})}{(SSW_l + SSW_{l'})/(N_l + N_{l'}-2)} \end{aligned} Pseudot2=(SSWl+SSWl′)/[(Nl+Nl′−2)]p[SSWM−(SSWl+SSWl′)]/p=(SSWl+SSWl′)/(Nl+Nl′−2)SSWM−(SSWl+SSWl′)
其中: S S W l SSW_l SSWl代表类别 l l l内的平方和, S S W l ′ SSW_{l'} SSWl′代表类别 l ′ l' l′的平方和, S S W M SSW_M SSWM代表类别 M M M的平方和。它的值越小,说明该合并步骤质量越高。
案例分析
iris聚类分析
k-means聚类分析
先使用k-means方法对原始数据进行分析:
分析的步骤:
-
首先取出数据的前四列,并且对数据进行标准化的预处理。这里的标准化是中心化标准化。
iris.4 = iris[, 1:4] iris.4 = scale(iris.4, center=T, scale=T) -
使用k均值聚类,这里我们默认使用的类别数是5。
分别得到每一类有:23 25 48 25 29个观测数据。
-
画图,关于花瓣和萼片。
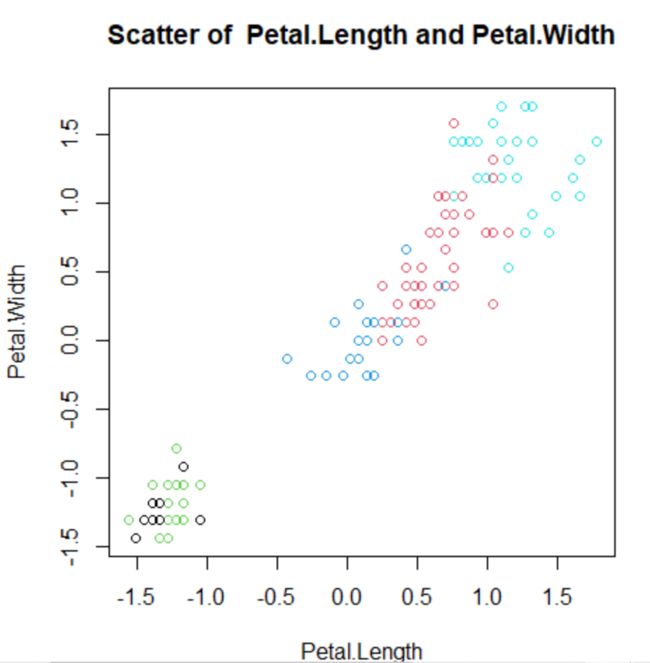 图1 花瓣的长度与宽度
图1 花瓣的长度与宽度
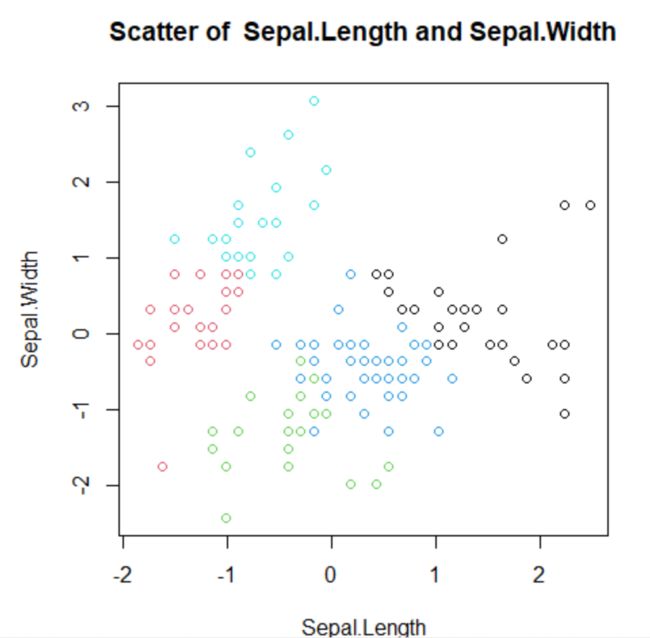 图2 萼片的长度与宽度
图2 萼片的长度与宽度
-
再通过伪F值,找到最优的K
在标准化之后,我们得到最优的k是2,但是在未标准化时,我们得到的最优k是3。画图如下:
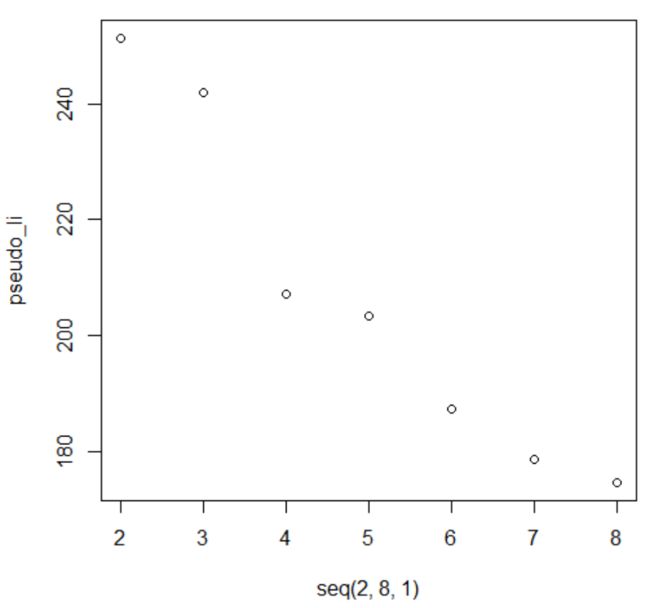 图1 标准化之后得到伪F值
图1 标准化之后得到伪F值
 图2 标准化之前得到伪F值
图2 标准化之前得到伪F值
标准化之后进行聚类得到的类别个数与原始数据中给出的类别个数不一,具体原因我猜想是这些不同变量之间的度量差异可能对他们的特征具有代表性,经过标准化之后会”泛化“这些”代表性“。
-
进行多维标度分析,将4维数据降为2维,画出类别的分布,这里是使用最优类别为3来画图的。

如图所示,数据之间还算分得开,其中左半部分代表第一类的数据分布,后半部分分别代表第三类和第二类的数据分布。
-
最后选择最优的类别个数为3.
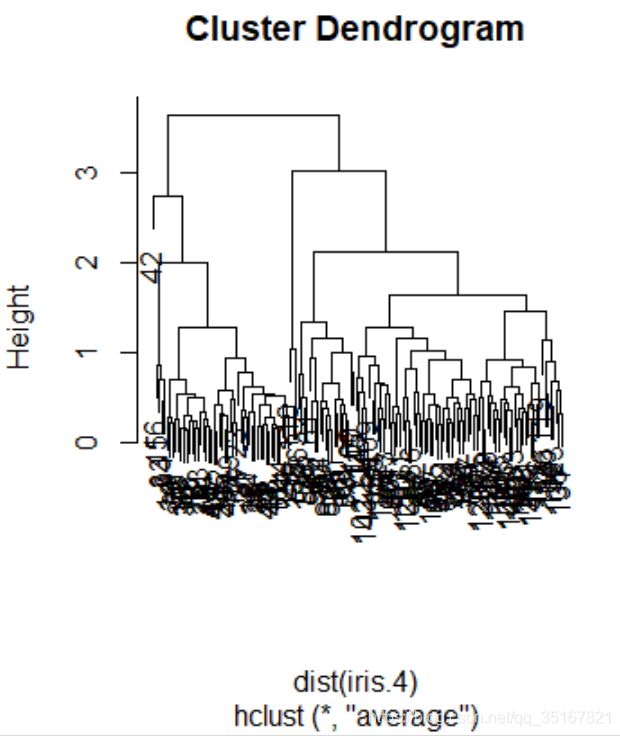
层次聚类法分析
分析的步骤:
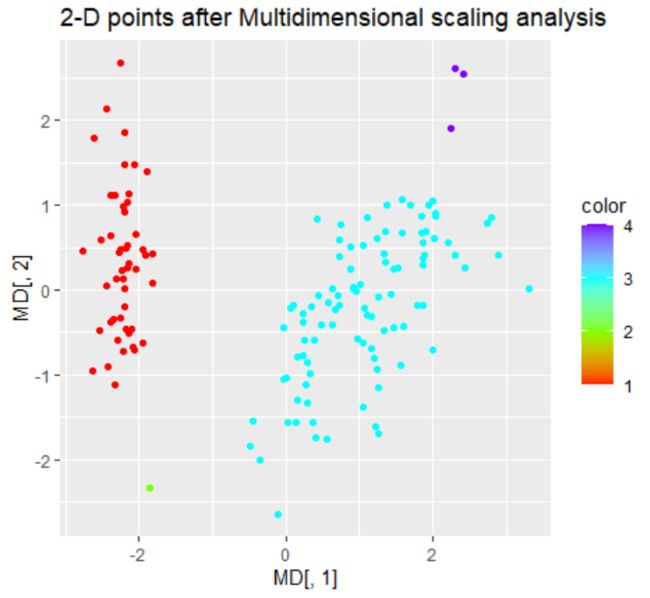 图1 类别数设置为2 图1 类别数设置为2
|
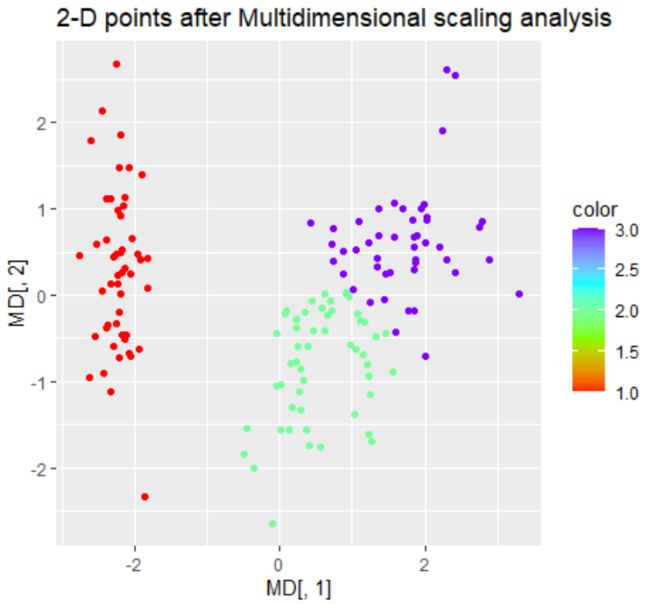 图2 类别数设置为4 图2 类别数设置为4
|
由图1所示,将类别数设置为4,各个类别的分布不太均匀,且分布离散,不太合适,结合层次聚类得到的图知,得到的类别只能为2、4、6等类,于是我们尝试将类别数仅设置为2,图像如图2所示.
-
使用NBclust,找到层次聚类分析法中的最优的类别个数:
这里使用控制方法分析,在使用NbClust分析的时候,method为average.
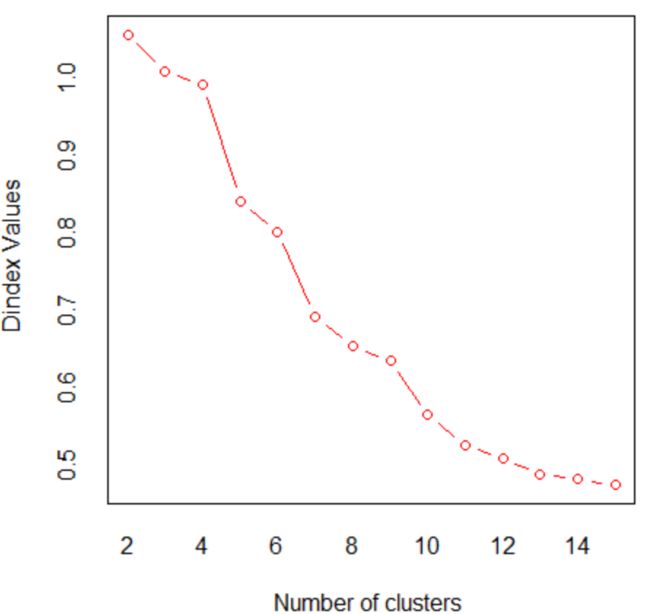 图1 索引值与类别个数
图1 索引值与类别个数
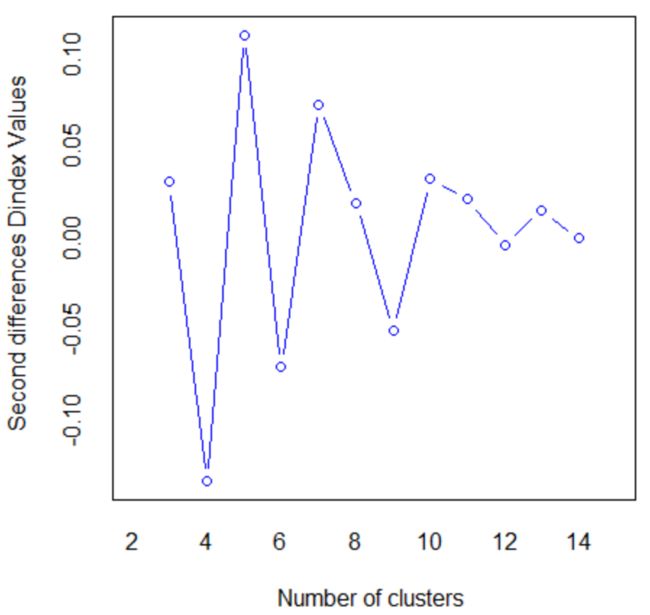 图2 索引值的二阶差分与类别个数
图2 索引值的二阶差分与类别个数
由左图可知,Dindex values的值随着类别个数的增大而减小。在这里,我们进行聚类分析时使用的index是“all”,index最大值所对应的类别个数是最优的类别个数,所以最终我们使用层次聚类法得到的类别个数为2. 同时,使用
nbcluster$Best.partition得到的最优类别个数也是2.
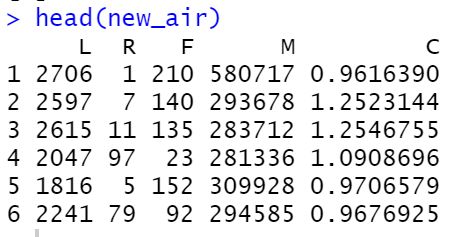
航空公司客户数据聚类分析
本次使用的对航空公司客户数据聚类分析使用的是LRFMC模型。
LRFMC模型变量解释:
| 模型 | L | R | F | M | C |
|---|---|---|---|---|---|
| 航空公司LRFMC模型 | LOAD_TIME - FFP_DATE会员入会时间距观测窗口结束的月数 | LAST_TO_END客户最近一次乘坐公司飞机距观测窗口结束的月数 | FLIGHT_COUNT客户在观测窗口内乘坐公司飞机的次数 | SEG_KM_SUM客户在观测窗口内累计的飞行里程 | AVG_DISCOUNT客户在观测窗口内乘坐舱位所对应的折扣系数的平均值 |
步骤:
-
标准化,因为L代表的是天数,不能取负值,所有这里标准化选择最大最小标准化。
-
聚类,使用k-means聚类,聚为5类:
其中1-5类分别有10267, 21734, 12221, 4976, 13786 .
-
画图:
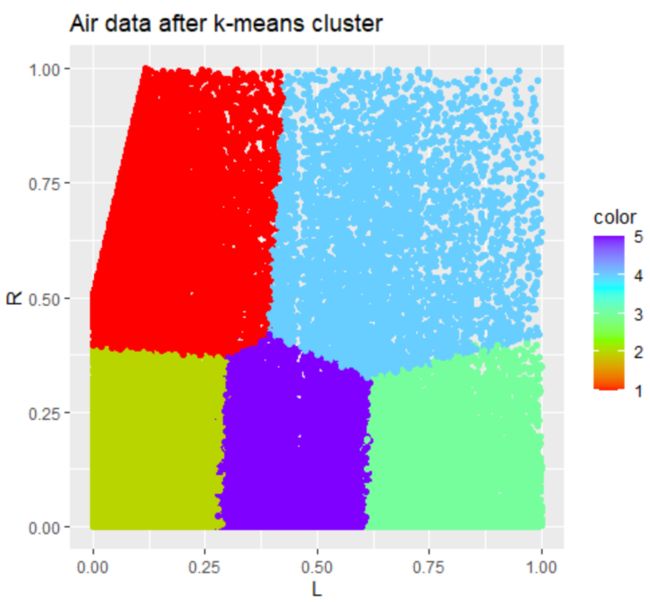
分别得到5类图的在L和R上的分布。
因为在本航空数据中,数据量过大,K-means法比较适用,层次聚类法不太适用,所以我们不考虑使用层次聚类法来进行聚类分析。
总结
本报告按照数据介绍、原理简介、案例分析(分为iris和air_data),最后的总结来展开。
其中在案例分析中,对iris数据,因为其数据量比较小,所以我们使用了两种方法来对数据进行聚类分析,但是这里仅仅只是对数据进行了聚类,没有比较两者之间的效果,在以后的学习过程中,需要补齐。除了对iris数据进行聚类之外,还结合了上一张聚类分析的内容,尝试使用多标度分析法来降维,对数据画图,通过可视化,对比了数据聚类的效果。
对于air_data数据,因为数据量比较大,所以只采用了k-means聚类方法来分析,分析的过程比较简单,在以后的学习中还需回来完善。
在找最优刻度上,只针对iris数据找了一下,但是在后来的air_data数据中就没有找,因为我发现这个Pseudo F值随着类别的增大是在不断减小的,且越来越小,我不知道类别取哪个值是合适的,所以就取了一个默认的数5,不严谨。
参考
[1] In scan(file = file, what = what, sep = sep, quote = quote, dec = dec, : EOF within quoted string
[2] 基于R语言的聚类分析(k-means,层次聚类)
[3] 请问如何用r语言中的ggplot2画出多种渐变色的好看的图?
[4] R语言计算某一列中变量种类以及每一个种类中的变量个数
[5] 航空公司客户价值分析
[6] 航空客户价值分析特色LRFMC模型——RFM升级
代码
# -----------1、获取数据并标准化
iris.4 = iris[, 1:4]
iris.4 = scale(iris.4, center=T, scale=T)
# -----------2、对前四列数据做聚类
##k均值聚类
K <- 4
cluster.iris <- kmeans(iris.4,centers = K,iter.max = 99,nstart=25)
cluster.iris$size
# -----------3、画图
plot(iris.4, col=cluster.iris$cluster)
plot_data = function(data, k=4){
# 找到前四列的数据
# 我希望来画图
# 将聚的类添加到最后一列
cluster.data <- kmeans(data,centers = 5,iter.max = 99,nstart=25)
print(length(cluster.data$cluster))
sepal = data[, 1:2]
petal = data[, 3:4]
color = cluster.data$cluster
plot(sepal, xlab=colnames(sepal)[1], ylab=colnames(sepal)[2],
main=paste("Scatter of " , colnames(sepal)[1], "and", colnames(sepal)[2]),
col=color)
plot(petal, xlab=colnames(petal)[1], ylab=colnames(petal)[2],
main=paste("Scatter of " , colnames(petal)[1] , "and", colnames(petal)[2]),
col=color)
return(data)
}
plot_data(iris.4)
# -----------4、找到最优刻度
N <- dim(iris.4)[1]
pseudo_li = seq(2, 8, 1)
i = 1
for (k in 2:8){
clustercars <- kmeans(iris.4,centers = k,iter.max = 99,nstart=25)
pseudo = (clustercars$betweenss / (k - 1)) / (clustercars$tot.withinss / (N - k))
pseudo_li[i] = pseudo
print(paste(k, ": ", pseudo))
i = i + 1
}
plot(seq(2, 8, 1), pseudo_li)
# -----------5、多维标度分析,清晰可视化
library(ggplot2)
# 1、对原始维度的变量进行k-means聚类
# 2、对聚类之后的数据,通过多维标度分析转化为2维
# 3、对2维数据画图,颜色为第几类变量
cluster.data <- kmeans(iris.4, centers = 3, iter.max = 99,nstart=25)
color = cluster.data$cluster
m.data = as.matrix(data[, 1:4])
dis.data = dist(m.data)
MD = cmdscale(dis.data, k=2)
p <- ggplot(data=as.data.frame(MD), mapping=aes(x=MD[, 1], y=MD[, 2]))
d <- p + geom_point(aes(colour=color)) + ggtitle(label="2-D points after Multidimensional scaling analysis") + scale_color_gradientn(colours =rainbow(4))
d
# ---------6、层次聚类法。
help("hclust")
tree <- hclust(dist(iris.4),method = "average")
# method="average"指定使用平均连接法。
# 画聚类树图。
plot(tree)
# 类别数为2时所得的聚类结果。
out <- cutree(tree,k = 2)
out
table(out) # 查看多少类
# -----------7、多维标度分析,查看层次聚类之后的结果
library(ggplot2)
m.data = as.matrix(iris.4)
dis.data = dist(m.data)
MD = cmdscale(dis.data, k=2)
color = out
p <- ggplot(data=as.data.frame(MD), mapping=aes(x=MD[, 1], y=MD[, 2]))
d <- p + geom_point(aes(colour=color)) + ggtitle(label="2-D points after Multidimensional scaling analysis")+ scale_color_gradientn(colours =rainbow(4))
d
# -----------8、使用NbClust函数进行聚类,实际是找最优类别数K
library(NbClust)
#加载程序包NbClust,其中含有NbClust函数。
help(NbClust)
nbcluster <- NbClust(iris.4,method = "average")
# "average",表示使用平均连接的层次聚类法),将数据进行聚类。
# 查看nbcluster包含的分析结果项
names(nbcluster)
# 查看综合各个指标所得的最佳类别数下,各个观测所属的类别
nbcluster$Best.partition
# =====================航空客户信息============================
# -----------读取数据
air_data = read.csv("D:/lagua/CODING/R-learn/R-code/Chap6_ClusterAnalysis/air_data.csv",
header=TRUE,quote = "",
sep=",",
encoding='UTF-8',
strip.white = TRUE
)
colnames(air_data)
col_need = c('LOAD_TIME', 'FFP_DATE','LAST_TO_END', 'FLIGHT_COUNT', 'SEG_KM_SUM', 'avg_discount')
air_data = subset(air_data, select=col_need)
air_data$LOAD_TIME = as.Date(air_data$LOAD_TIME)
air_data$FFP_DATE = as.Date(air_data$FFP_DATE)
str(air_data)
library(dplyr)
# -----------1、数据预处理
# 1 初始化数据
# 2 将数据转化成整数,转化为数值型
# 3 删除列
# 4 重新命名
# 5 对列重新排序
new_air = air_data
new_air = na.omit(new_air)
new_air$L = (new_air$LOAD_TIME - new_air$FFP_DATE) %>% as.numeric()
new_air$FLIGHT_COUNT = as.numeric(new_air$FLIGHT_COUNT)
new_air = new_air[,-which(names(new_air) %in% c('LOAD_TIME', 'FFP_DATE'))]
new_air = rename(new_air, c("R"='LAST_TO_END', "F"='FLIGHT_COUNT', "M"='SEG_KM_SUM', 'C'='avg_discount'))
new_air = new_air[, c(5, 1, 2, 3, 4)]
colnames(new_air)
head(new_air)
str(new_air)
# 最大最小标准化
normalize <- function(x) {
return((x - min(x)) / (max(x) - min(x)))
}
std_air = apply(new_air, 2, normalize)
head(std_air)
# L = LOAD_DATE - FFP_DATE
# R = LAST_TO_END
# F = FLIGHT_COUNT
# M = SEG_KM_SUM
# C = AVG_DISCOUNT
# -----------2、k均值聚类
K <- 5
clusterair <- kmeans(std_air,centers = K,iter.max = 99,nstart=25)
table(col=clusterair$cluster)
# -----------3、画图
color = clusterair$cluster
L <- std_air[, 1]
R <- std_air[, 2]
p <- ggplot(data=as.data.frame(std_air), mapping=aes(x=L, y=R))
d <- p + geom_point(aes(colour=color)) + ggtitle(label="Air data after k-means cluster")+ scale_color_gradientn(colours =rainbow(4))
d
plot(std_air, col=clusterair$cluster)