LDA主题模型读书笔记（一）

前言

这几天在补主题模型LDA，看的我晕头转向的，最后梳理清楚思路后有以下几点感悟：

• LDA模型总的来看涉及到三方面知识：1.概率论知识；2.LDA自身的基本建模思想；3.Gibbs采样。
• 为什么看得头晕？是因为我们总是把这三方面知识杂糅在一起了，其实把这几方面分开缕清楚，同时不去钻一些牛角尖的话（Dirichlet分布和Gibbs采样理论推导等），问题就简单多了。
• 很多文章侧重在1和3上，却忽视了2，导致大家看了半天LDA都不知道目标函数是什么，其实这才是首要需要弄明白的。

在进入正题之前，还是把有关LDA模型的两篇中文经典文章列一下，强烈建议阅读。（本文主要还是帮助大家缕清思路的一个读书笔记性质的文章）

正文

LDA的目标是什么？

大家当然会说是提取文章的多个主题，这个当然没错啦。

但对于建模来说，首先要弄清楚它的目标函数是什么，个人认为从广义上来说，LDA的目标和传统语言模型是类似的，就是找到一组参数，使得当前语料生成的概率最大。（极大似然估计）

这个目标函数看起来好像和"主题"没什么关系。实际上，这个目标函数的一个最朴素的建模确实和"主题"没关系，由此引出第一个最简单的模型：

统计学派的unigram 假设

假设我们有一个字典V，我们每次从中重复抽样一个单词，抽取N次后会生成一个文本d。
根据统计学派的理论，我们可以假设单词的每次抽取都是独立同分布的，并且服从多项式分布。（就是说每次抽取每个单词的概率都是固定的，只是我们事先不知道这些概率是多少，需要通过观测到的结果来估计）。

如此我们便可以生成一个文本，这个文本生成的概率是：

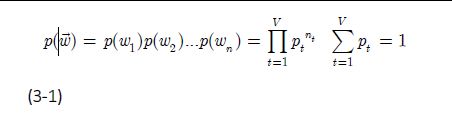
根据极大似然估计，我们要使得这个文本生成的概率最大化，求解后可得到每个词被抽取的概率$p_i=n_i/N$(公式不太严谨，自信体会）。
显然这样计算得到的概率值有很强的巧合性，更一般的我们可以生成M篇文档，每篇文档有Ni个词。（实际情况一般是我们已经有M篇文档了，然后对文档进行分词，由此可以根据上面的方法估计出每个词概率的多项分布）。

贝叶斯学派的unigram 假设

我们再对上面的unigram假设用一个更形象的方式来描述。
假设我们现在有一个骰子，这个筛子有V（字典大小）面，我们每次掷骰子就能生成一个词，只是这个骰子并不是均匀的（每个面出现的概率是不一样的）我们要做的就是根据观测结果估计每个面出现的概率。

但贝叶斯学派的认为这是不对的，他们认为一开始有很多个筛子，这些筛子服从Dirichlet分布（因为Dirichlet 分布式是多项分布的共轭先验，意思就是***），Dirichlet 分布有一个先验超参数向量$\alpha$，我们每次会从其中随机抽一个骰子出来，然后再像统计学派那样去掷骰子。

最终我们根据生成的文本，可以根据最大后验估计出每个词的概率分布的期望值：

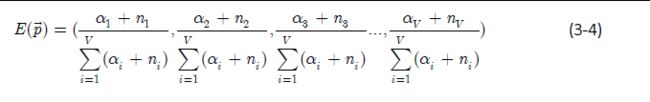
直观上和极大使然估计其实很像，区别在于：

• 前者是计算的概率，后者是计算的概率期望。
• 前者无先验超参数，后者引入了先验超参数。

ps:这只是表面上的区别，更详细的推导参考上诉文章。

小结：
我们可以看到，这两个建模其实都没有涉及到"主题"，就是单纯的根据已经存在的语料，对每个词的抽取概率进行了估计，从而这个语料出现的概率最大化。

LDA模型

首先说明，LDA模型是基于贝叶斯学派的。
另外，LDA假设每个词是由它背后的一个潜在的主题中抽取出来，而不是直接从词表中抽取的，整个流程可以由下图表示：

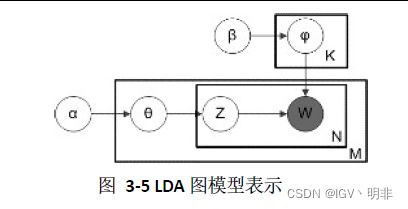
对于这个图的具体解释大家还是可以参考文章，这里不再赘诉，只是为了方便描述文本生成的流程：

 抽取K个服从Dirichlet分布的主题词骰子。
 for i in range(M):
 	对于第i个文档，抽取1个服从Dirichlet分布的文档主题骰子。
	for j in range(N):
		对于第i个文档的第j个词：
		i.先掷文档主题的骰子，生成主题。
		ii.根据生成的主题，掷相应的主题词骰子，生成对应的词。

我们的目标依旧没变，还是最大化$p(w)$，而最大化$p(w)$就是求这些参数。
实际上，LDA模型希望得到的是$p(z|w)$，也就是每个词属于每个主题的概率分布，不过只要求解出所有参数自然也能得到这个条件概率。
但此时问题却出现了：

所以我们需要一个近似求解方法，这也就诞生出了Gibbs采样。

Gibbs采样是什么？

为了解释这个，首先需要了解一些别的知识。

蒙特卡罗方法

统计模拟中有一个重要的问题就是给定一个概率分布$p(x)$，我们如何在计算机中生成它的样本。一般而言均匀分布的样本是相对容易生成的。 通过线性同余发生器可以生成伪随机数。
不过我们并不是总是这么幸运的，当$p(x)$的形式很复杂，或者是个高维的分布的时候，样本的生成就可能很困难了,此时就需要使用一些更加复杂的随机模拟的方法来生成样本。而本 MCMC(Markov Chain Monte Carlo) 和 Gibbs Sampling算法就是最常用的一种。

马尔可夫链

马尔可夫链条通俗说就是根据一个转移概率矩阵去转移的随机过程，且状态转移的概率只依赖于前一个状态。
有这么一种情况，初始位置向量在经过若干次转移后会达到一个稳定状态，之后再
转移概率分布也不变化了，这个状态称之为马尔科夫链的平稳分布$\pi$。

Gibbs Sample

对于给定的概率分布$p(x)$,我们希望能有便捷的方式生成它对应的样本。由于马氏链能收敛到平稳分布， 于是一个很的漂亮想法是：如果我们能构造一个转移矩阵为$P$的马氏链，使得该马氏链的平稳分布恰好是$p(x)$, 那么我们从任何一个初始状态$x_1$出发沿着马氏链转移, 得到一个转移序列$x_1,x_2...,x_n,x_{n+1}$， 如果马氏链在第n步已经收敛了，于是我们就得到了 平稳分布$\pi (i)$ 的样本$x_n,x_{n+1}...$。

这里就不再赘诉采样方法的演进，这里直接给出Gibbs sample的公式：

LDA模型的Gibbs sample推导

所以对于LDA模型的Gibbs sample，我们只需要明确两个东西：

1. 对于LDA模型而言，采样的对象是什么？答：对于第$i$篇文章第$j$个词，这个词所属的主题，即sample $z$~$p(z_{ij}|z_{-ij},w)$
2. 采样必须是对一个概率分布采样，这里的概率分布是什么？答：就是$p(w,z)$的联合分布。

由此我们便可以推导出LDA模型中Gibbs Sampling的核心公式了：

而这俩参数可以通过Dirichlet参数估计得到：

这个公式是很漂亮的， 右边其实就是$p(doc|topic)\ast p(topic|word)$，这个概率其实是doc->topic->word的路径概率。经过有限次采样后，采样样本会趋于一个平稳分布。

LDA模型Gibbs sample实现流程

这个实现的逻辑其实上述的文章写的很清楚了，一个是侧重于整个的流程，另一个是用伪代码的形式，二者都值得一看。
这里我就复述下《LDA数学八卦》作者rickjin的描述：
有了 LDA 模型，当然我们的目标有两个：

• 估计模型中的参数 ${\varphi }_{1,2...,K}$ 和 ${\theta }_{1,2...,M}$；
• 对于新来的一篇文档，我们能够计算这篇文档的 topic 分布${\theta }_{new}$。

有了 Gibbs Sampling 公式， 我们就可以基于语料训练 LDA 模型:

由这个topic-word 频率矩阵我们可以计算每一个$p(word|topic)$概率，从而算出模型参数${\varphi }_{1,2...,K}$, 这就是上帝用的K个 topic-word 骰子。同理可以估计出${\theta }_{1,2...,M}$。

有了 LDA 的模型，对于新来的文档 $do{c}_{new}$, 我们如何做该文档的 topic 语义分布的计算呢？基本上 inference 的过程和 training 的过程完全类似。对于新的文档， 我们只要认为 Gibbs Sampling 公式中的 ${\varphi }_{1,2...,K}$ 部分是稳定不变的，是由训练语料得到的模型提供的，所以采样过程中我们只要估计该文档的 topic 分布就好了：