基于惯性权值非线性递减的改进粒子群算法 - 附代码
基于惯性权值非线性递减的改进粒子群算法
文章目录
- 基于惯性权值非线性递减的改进粒子群算法
-
- 1.粒子群优化算法
- 2. 改进粒子群算法
-
- 2.1 惯性权值非线性变化策略
- 2.2 粒子最大速度非线性递减策略
- 2.3 自然选择原理
- 2.4 粒子二阶振荡策略
- 3.实验结果
- 4.参考文献
- 5.Matlab代码
- 6.Python代码
摘要:针对粒子群优化算法中出现的收敛早熟和不收敛的问题,提出了一种基于自然选择和惯性权值非线性递减的改进粒子群算法,在算法迭代过程中,粒子边界速度采用最大速度非线性递减变化策略来限制,惯性权值非线性递减变化用于平衡种群粒子前期全局搜索与后期局部寻优的能力;为使种群在进化过程中保持多样性,在标准粒子群算法中引用二阶振荡策略使种群在进化过程中始终保持着多样性;在此基础上,进一步地将遗传算法中的选择机理与粒子群算法结合起来用于提高算法的适用性能;
1.粒子群优化算法
基础粒子群算法的具体原理参考网络资料
2. 改进粒子群算法
2.1 惯性权值非线性变化策略
惯性权重是 PSO 算法中极其重要的参数, 它描 述了粒子上一代速度对当前代速度的影响, 按制其 取值大小可有效地调节平衡 PSO 算法的全局与局 部寻优能力。当惯性权值较大时, 全局寻优能力较 强, 局部寻优能力较弱; 当惯性权重较小时, 局部寻 优能力较强, 而全局寻优能力将减弱。考虑切比雪 夫滤波器幅频响应曲线模型在线性和非线性行为之 间表现出极好的过渡性, 提出了一种基于切比雪夫 滤波器惯性权重非线性变化策略, 并引入权重控制 因子, 通过调节该控制因子的大小进而来调整最大 惯性权值在种群进化过程中所占的比例, 能够保证 粒子群在初始状态时以较大的惯性权值进行全局开 发性搜索, 而在迭代后期又以较小的固定权值进行 更为精细化的局部寻优, 其数学模型如式 (5) 所示:
w ( t ) = 0.55 1 + ( K t T ) 10 + 0.4 (5) w(t)=\frac{0.55}{\sqrt{1+\left(\frac{K t}{T}\right)^{10}}}+0.4 \tag{5} w(t)=1+(TKt)100.55+0.4(5)
其中,K 为权重控制因子,t 为种群当前进化代数,T为种群总的进化代数。在算法迭代初始,粒子的权值可以取得最大值 0. 95,有利于前期的全局搜索,而随着迭代次数的增加,粒子的权值逐渐趋近最小值 0. 4,此时可以更好地进行局部精细化搜索。
2.2 粒子最大速度非线性递减策略
粒子最大速度的设置非常重要, 较大的速度有 利于种群进行全局的开发, 但粒子速度过大, 会导致 粒子在搜索的过程中错过全局最优解; 与之相反, 较 小的速度有助于种群进行局部搜索, 但速度过小, 会 导致粒子不能够在解空间内进行充分探索, 从而陷 入局部最优的可能性提高。为了进一步提高 PSO 算法的性能, 防止因为粒子飞离搜索空间而造成种 群多样性减小, 进而提出了一种粒子最大速度非线 性递減策略。粒子的最大速度在随着种群迭代的进 行过程中呈现非线性减小, 可使粒子有效地避免因为 过大的速度而落入边界区域进行无效地搜索。粒子 最大速度非线性递减策略数学模型如式 (6) 所示:
V max ( t ) = v max 1 + ( 3 t T ) 10 + v min (6) V_{\max }(t)=\frac{v_{\max }}{\sqrt{1+\left(\frac{3 t}{T}\right)^{10}}}+v_{\min } \tag{6} Vmax(t)=1+(T3t)10vmax+vmin(6)
其中, v max v_{\text {max }} vmax 与 v min v_{\text {min }} vmin 分别为种群粒子最大速度的最大值 与最小值, 它们的取值由标准测试函数定义域确定。
2.3 自然选择原理
考虑到 PSO 算法优化性能会受到的随机因素影响较多,为了提高算法的适用性,结合遗传算法中
的选择思想,在上述几种改进策略的基础上加入自然选择机制,其基本思想为每次迭代过程中将整个粒子群按照适应值的大小来进行排序,并用群体中适应值最好的一半的粒子的速度与位置来替换群体中适应值最差的一半的粒子的位置和速度,在这一过程中保留原来个体记忆的最优值,来提高粒子接近最优值的几率。
2.4 粒子二阶振荡策略
粒子群算法在迭代过程中是呈现渐进收敛的,整个迭代过程中种群的多样性势必会有减小的趋势,这不利于粒子寻求最优解的几率提高,在标准粒子群算法的基础上,采用文献[11]中所述的方法,对粒子速度更新进行二阶振荡处理,以进一步提高种群的多样性,改善算法的全局与局部收敛平衡性能。其速度更新方程如下:
v i d k + 1 = w v i d k + c 1 r 1 [ p i d − ( 1 + ξ 1 ) x i d k + ξ 1 x i d k − 1 ] + c 2 r 2 [ p g d − ( 1 + ξ 2 ) x i d k + ξ 2 x i d k − 1 ] (7) v_{i d}^{k+1}=w v_{i d}^{k}+c_{1} r_{1}\left[p_{i d}-\left(1+\xi_{1}\right) x_{i d}^{k}+\xi_{1} x_{i d}^{k-1}\right]+c_{2} r_{2}\left[p_{g d}-\left(1+\xi_{2}\right) x_{i d}^{k}+\xi_{2} x_{i d}^{k-1}\right] \tag{7} vidk+1=wvidk+c1r1[pid−(1+ξ1)xidk+ξ1xidk−1]+c2r2[pgd−(1+ξ2)xidk+ξ2xidk−1](7)
其中, ξ 1 \xi_{1} ξ1 与 ξ 2 \xi_{2} ξ2 为随机数。根据文献 [ 12 ] [12] [12], 为使算法 在迭代前期具有较强的全局搜索能力, 取 ξ 1 ⩽ \xi_{1} \leqslant ξ1⩽ 2 c 1 r 1 − 1 c 1 r 1 , ξ 2 ⩽ 2 c 2 r 2 − 1 c 2 r 2 \frac{2 \sqrt{c_{1} r_{1}}-1}{c_{1} r_{1}}, \xi_{2} \leqslant \frac{2 \sqrt{c_{2} r_{2}}-1}{c_{2} r_{2}} c1r12c1r1−1,ξ2⩽c2r22c2r2−1; 为使算法在迭代后期具 有较强的局部搜索能力能够渐进收玫, 取 ξ 1 ⩾ \xi_{1} \geqslant ξ1⩾ 2 c 1 r 1 − 1 c 1 r 1 , ξ 2 ⩾ 2 c 2 r 2 − 1 c 2 r 2 \frac{2 \sqrt{c_{1} r_{1}}-1}{c_{1} r_{1}}, \xi_{2} \geqslant \frac{2 \sqrt{c_{2} r_{2}}-1}{c_{2} r_{2}} c1r12c1r1−1,ξ2⩾c2r22c2r2−1, 这里的算法迭代前期指 的是进化代数小于或等于最大进化代数的一半。
改进粒子群算法的主要实现步骤如下:
(1) 设定各参数, 初始化种群中各粒子的位置 和速度;
(2)计算种群中每个粒子的适应度值, 初始化 种群个体最优值和全局最优值, 将当前各粒子的位 置和适应度值存储在各个粒子的 p i p_{i} pi, 将当前所有 pbest 中适应度值最优个体的位置和适应度值存储 于 p g p_{g} pg 中;
(3)根据式 (5) 对惯性权值进行更新;
(4)根据式(7)以及式(1)中的位置更新公式 进行粒子的速度和位置更新;
(5)根据式(6)对粒子的最大速度进行更新, 以保证算法的收敛性能;
(6)比较粒子适应度值与其经历过的最好的位 置进行比较, 更新粒子当前的个体最优值;
(7)比较粒子适应度值与种群全局极值, 更新 粒子当前的全局最优值;
(8) 将种群适应度值的大小进行排序, 用群体 中最好的一半的粒子的速度和位置替换最差的一半 的粒子的速度和位置, 同时把持种群中个体最优值 与全局最优值记忆不变;
(9)若满足迭代停止条件, 则搜索结束; 若不满 足迭代停止条件, 则返回步骤 (3)。
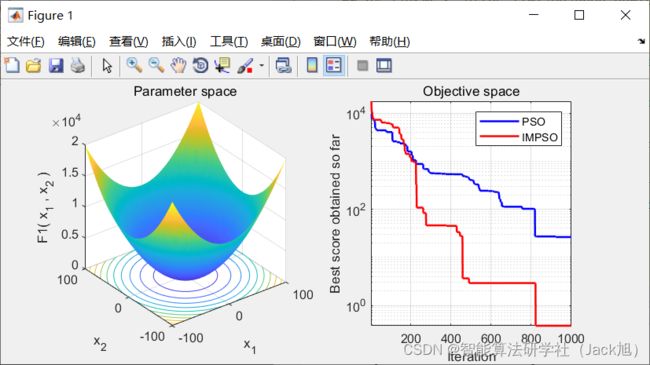
3.实验结果
4.参考文献
[1]华勇,王双园,白国振,李炳初.基于惯性权值非线性递减的改进粒子群算法[J].重庆工商大学学报(自然科学版),2021,38(02):1-9.