ML----一文入门机器学习

1. 前言

这篇文章其实是人工智能程序员面试笔试宝典第一章的笔记。不同的是，它提到的大多数知识点我都作了实现。书中有部分老代码已经跑不通了，我给它改了一下；有些地方一笔略过，但是我感觉有用的也写了代码。还有一些待完善的地方，后续会继续增加内容的。

书链接：豆瓣

2. 分类

2.1. 任务类型

• 回归模型 : 预测某个无法枚举的数值,例如股价预测.
• 分类模型 : 将样本分为n个类别,如信用风险异常识别
• 结构化学习模型

学习链接

应用的领域包括: 语音识别\翻译\语法分析\目标检测\Summarization\Retrieval

2.2. 学习理论

• 有监督学习

训练样本带标签

值得一提的是,自监督学习也是有监督学习.

• 半监督学习

训练样本部分有标签

• 无监督学习

训练样本全部无标签

• 强化学习

智能体(Agent)通过与环境进行交互获得的奖赏来指导自己的行为,最终目标是使智能体获得最大的奖赏.

与监督学习不同的是,强化学习中由环境提供的强化信号是对产生对坐的好坏的一种评价,而不是告诉强化学习系统如何去产生正确的动作.

• 迁移学习

运用已有的知识或者数据对不同但有关联的领域问题进行求解.

2.3. 判别式与生成式

• 判别方法

学习决策函数$Y=f(X)$,或者学习分布概率$Y=P(Y|X)$

常见的包括线性回归,boosting,SVM,决策树,感知机,线性判别分析(LDA),逻辑斯蒂回归算法等.

• 生成方法

由数据学习$x$和$y$的联合概率密度分布函数$P(Y,X)$,然后通过贝叶斯公式求出条件概率分布$P(Y|X)$作为预测的模型为生成模型. 常见的生成模型有朴素贝叶斯 隐马尔科夫模型,高斯混合模型,文档主题生成模型LDA等.

3. 性能度量

3.1. 回归问题

3.1.1. 均方误差

$$MSE=\frac{1}{n}\sum _{i=0}^n(f(x_i)-y_i{)}^2$$

3.1.2. Root Mean Squared Error RMSE

均方根误差

它是观测值与真值偏差的平方和与观测次数m比值的平方根,用来衡量观测值同真值之间的偏差

$RMSE=\sqrt{MSE}=\sqrt{\frac{1}{n}\sum _{i=0}^n(f(x_i)-y_i{)}^2}$

3.1.3. 和方误差

$SSE=\sum _{i=0}^n(f(x_i)-y_i{)}^2$

3.1.4. MAE Mean Absolute Error(MAE)

直接计算模型输出与真实值之间的平均绝对误差

$MAE=\frac{1}{n}\left|\sum _{i=0}^{n}f(x_i)-y_i\right|$

3.1.5. Mean Absolute Percentage Error(MAPE)

这个方法不见考虑预测值与真实值之间的误差,还考虑了误差与真实值之间的比例

$MAPE=\frac{1}{n}\sum _{i=0}^n\frac{|f(x_i)-y_i|}{y_i}$

3.1.6. 平均平方百分比误差

$\mathrm{MASE}=\frac{1}{n}{\sum }_{i=0}^n{\left(\frac{|f\left(x_i\right)-y_i|}{y_i}\right)}^2$

3.1.7. 决定系数

$R^2=1-\frac{\mathrm{S}\mathrm{S}\mathrm{E}}{\mathrm{S}\mathrm{S}\mathrm{T}}$, 其中 $\mathrm{S}\mathrm{S}\mathrm{T}={\sum }_{i=0}^n{\left(y_i-\bar{y}\right)}^2$

3.2. 分类问题

常用的包括:

• 精确率
• 召回率
• F1
• TPR
• FPR

	预测为真	预测为假
真实为真	TP	FN
真实为假	FP	TN

• FP false negative
• FP false positive
• TN true negative
• FN false negative

计算方式为:

3.2.1. 精确率

$Precision=\frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{P}}$

精确率又称为查准率,适用于需要精度高的场景,例如网页推荐.

3.2.2. 召回率

召回率又称为查准率,适用于检测信贷风险,逃犯信息等.

$Recall=\frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N}}$

3.2.3. F1 一种折中

由于精确率和召回率是一对相互矛盾的值,所以需要一种折中以确定相对较优的评价指标

$\frac{1}{F_1}=\frac{1}{2}\ast \frac{1}{P}+\frac{1}{2}\ast \frac{1}{R}$

F1值是精确率和召回率的调和平均值

3.2.4. ROC曲线与AUC

对于0,1分类问题,一些分类器得到的结果并不是0,1,而是一个(0,1)之间的概率值,这个时候需要确定一个阈值cutoff , 当大于这个阈值的时候,将其归为1,否则归为0.

众所周知,TPR(True Positive rate)和FPR(False Positive Rate)是完相反的两个值,为了找到合适的分类阈值,应该直接从正确率上面着手,于是我们分别以TPR和FPR为横纵坐标绘制曲线,观察寻找合适的阈值cutoff

ROC曲线越靠近左上角，模型的查全率就越高。最靠近左上角的ROC曲线上的点是分类错误最少的最好阈值，其假正例和假反例总数最少。

#!/usr/bin/env python
# coding: utf-8

import os

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import xgboost as xgb
from sklearn.metrics import accuracy_score, roc_auc_score, roc_curve
from sklearn.model_selection import train_test_split

x1 = np.arange(0, 100, 1)
a = 0.3 * x1 + 1
b = 0.3 * x1 - 1
x2 = np.concatenate((a[0:50], b[50:]), axis=0)


data = []
idx = 0
for a_t, b_t in zip(x1.tolist(), x2.tolist()):
    if idx < 50:
        data.append((a_t, b_t, 0))
    else:
        data.append((a_t, b_t, 1))
    idx += 1
data = pd.DataFrame(data, columns=["x1", "x2", "label"])


sns.scatterplot(data["x1"], data["x2"], hue=data["label"])
plt.show()


x_train = data[["x1", "x2"]].values
y_train = data["label"].values.astype("int")

x_train, x_test, y_train, y_test = train_test_split(x_train, y_train, test_size=0.3)


dtrain = xgb.DMatrix(x_train, label=y_train)
dtest = xgb.DMatrix(x_test, label=y_test)

param = {"max_depth": 2, "eta": 1, "objective": "binary:logistic"}  # 设置XGB的参数，使用字典形式传入
num_round = 2  # 使用线程数
bst = xgb.train(param, dtrain, num_round)  # 训练
preds = bst.predict(dtest)  # 预测
# preds = np.array([1 if e>0.5 else 0 for e in preds])
# accuracy_score(preds,y_test)


roc_auc_score(y_test, preds)

fpr, tpr, thresholds = roc_curve(y_test, preds, pos_label=1)

thresholds

如果上述结果理解不了的话,参考一篇博客:roc_curve解析

4. 特征工程

4.1. 数据预处理

4.1.1. 无量纲化,数据缩放

标准化和最大最小缩放法,将所有的数据缩放到同一个维度.

其对应的公式分别为:

• 标准化$x^{\prime }=\frac{x-\mu }{\sigma }$
• 最大最小缩放 $x^{\prime }=\frac{x-\mu }{\sigma }$

其代码分别为:

import numpy as np 
import pandas as pd 

from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler

x = np.array([0.2,10000,80])
x = x.reshape(-1,1)
x1 = StandardScaler().fit_transform(x)
x2 = MinMaxScaler().fit_transform(x)

x,x1,x2

一般来说,选择标准缩放会更好一点,因为可以避免0值的出现.

4.1.2. 数据编码

主要针对文本类型的数据进行编码

常用的编码方式为独热(one-hot)编码.

中	美	德	法
1000	0100	0010	0001

代码如下:

import numpy as np 
import pandas as pd 
from sklearn.preprocessing import OneHotEncoder
from sklearn.preprocessing import LabelEncoder

df = pd.DataFrame([('中',),('美',),('德',),('法',)],columns=['country'])
df['country'] = LabelEncoder().fit_transform(df['country'])
temp = OneHotEncoder().fit_transform(df['country'].values.reshape(-1,1))
temp.toarray()

4.1.3. 缺失值补充

常用的策略

• 用异常值填充(如0,-9999)并将缺失值作为一个特征处理.

• 用均值或者条件均值填充.

• 用相邻数据填充

• 利用插值算法

• 数据拟合:利用非空数据构建模型,缺失值用拟合值填充

4.2. 特征选择

4.2.1. 方差选择法

核心思想为,如果某一列的数值特征变化一直很平缓,说明这个特征对结果的影响很小,所以可以计算各个特征的发叉,选择方差大于自设定阈值的特征.

代码如下:

1. 首先,确定大致的方差范围

from sklearn.feature_selection import VarianceThreshold
import os 
import numpy as np 
import pandas as pd 

file = "../data/iris.csv"

data = pd.read_csv(file,header=None)
data.columns = ['f1','f2','f3','f4','label']
data.describe()

我们选定阈值为0.64(0.8*的平方)

from sklearn.feature_selection import VarianceThreshold

VarianceThreshold(threshold=0.64).fit_transform(data[['f1','f2','f3','f4']].values)

最后得到的特征如下:

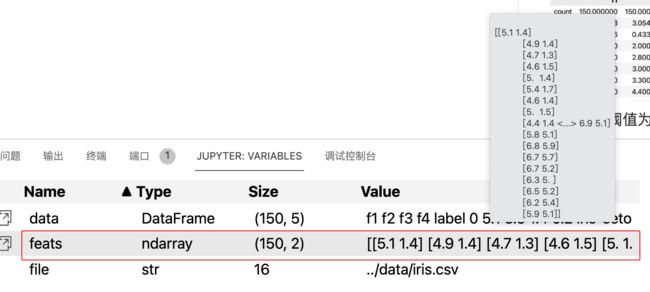
可以看到,最后留下了两个特征方差大于0.64的特征,并返回ndarray格式的数据.

4.2.2. 相关系数,统计检验

相关系数或者统计检验都可以用来进行特征选择,常用的有pearson相关系数和卡方检验,前者主要应用于连续变量,后者用于离散变量等.

• pearson相关系数代码如下:

from sklearn.feature_selection import SelectKBest
from scipy.stats import pearsonr
from sklearn.preprocessing import LabelEncoder
# pearson 相关系数

from sklearn.feature_selection import chi2
import pandas as pd 
import numpy as np 

file = "../data/iris.csv"

data = pd.read_csv(file,header=None)
data.columns = ['f1','f2','f3','f4','label']
data.describe()

feats = data[['f1','f2','f3','f4']]
x = feats
y = data['label'].values


# 卡方检验
# SelectKBest(lambda X,Y : np.array(map(lambda x:pearsonr(x,Y),X.T)).T,k=2).fit_transform(x,y)

SelectKBest(chi2,k=2).fit_transform(x,y)

4.2.3. 互信息法

互信息法经常用来评价自变量对因变量的相关性,互信息计算公式如下:

$I(X;Y)={\sum }_{x\in X}{\sum }_{y\in Y}p(x,y)\log \frac{p(x,y)}{p(x)p(y)}$

4.2.4. 基于机器学习的特征选择法

这种方法主要是针对特征和响应变量建立预测模型,例如用基于树的方法(决策树,随机森林,GBDT),或者扩展线性模型等.代码如下:

from sklearn.feature_selection import SelectFromModel
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.preprocessing import LabelEncoder

x = data[['f1','f2','f3','f4']].values
y = LabelEncoder().fit_transform(data['label'])

SelectFromModel(GradientBoostingClassifier()).fit_transform(x,y)

基于机器学习的方法,除了直接选择特征之外,还可以对特征进行降维之后进行特征选择.

• 基尼系数

基尼系数是一种衡量特征贡献值大小的方法.

在利用随机森林算法评估特征变量重要性的时候,主要依据每个特征变量在随机森林中的每棵树上做了多大的贡献,然后取平均值,最后比较不同特征之间的贡献值大小.基尼系数就是一种有效评估指标.

特征的重要性用$V$来表示,假设有$m$个特征$X_1,X_2,...,X_m$,则每个特征$X_j$的Gini指数记为$V_j$

${\mathrm{Gini}}_m=1-{\sum }_{k=1}^K{p}_{mk}^2$

其中k表示第k个类别,$P_{km}$表示节点m中,K表示分类个数.

特征变量$X_j$在节点m的重要性,即结点m分支前后的Gini指数变化量为:

$V_{jm}^{Gini}={\mathrm{Gini}}_m-{\mathrm{Gini}}_l-{\mathrm{Gini}}_r$

如果特征$x_j$在决策树$i$中出现的节点在集合M中,那么$X_j$在第$i$棵树的重要性为:

$V_{jm}^{Gini}={\sum }_{m\in M}{V}_{jm}^{Gini}$

假设随机森林共有n棵树,那么:

$V_{jm}^{Gini}={\sum }_{i=1}^n{V}_{ij}^{Gini}$

最后将所有求得的重要性评分进行归一化处理得到重要性评分:

$V_j^{\ast }=\frac{V_j}{{\sum }_{i=1}^c{V}_i}$

看起来很麻烦对不对,但其实这些原理和细节在sklearn库中已经实现,我们只需要调用即可,下面是代码:

from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier

x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=0)
forest = RandomForestClassifier(n_estimators=1000,random_state=0,n_jobs=-1)
forest.fit(x_train,y_train)
importances = forest.feature_importances_
importances

4.3. 特征降维

为了算法的计算效率,通常会将高维特征转化为较低的维度,并尽量使得各个特征之间无关联.

常用的降维算法包括:

4.3.1. PCA 主成分分析

将数据从一个维度变换到新的坐标系统中的线性变换.使得任何数据投影的第一大方差在第一个坐标(第一个主成分)上,以此类推.

其算法的计算步骤:

1. 计算相关系数矩阵

$$R=\left[\begin{array}{ccc}{r}_{11}& \cdots & r_{1p}\\ ⋮& & ⋮\\ r_{p1}& \cdots & r_{pp}\end{array}\right]$$

其中任意一个元素

$$r_{ij}=\frac{{\sum }_{k=1}^n\left(x_{ki}-{\bar{x}}_i\right)\left(x_{kj}-{\bar{x}}_j\right)}{{\sum }_{k=1}^n{\left(x_{ki}-{\bar{x}}_i\right)}^2{\left(x_{kj}-{\bar{x}}_j\right)}^2}$$

其代表的是两个特征$x_i$与$x_j$的相关系数.

2. 计算特征值与特征向量

解特征方程$\left|\lambda I-R\right|$,用雅克比法求出特征特征值,并使其按大小顺序排列: ${\lambda }_1⩾{\lambda }_2⩾\dots ⩾{\lambda }_p⩾0$,特征值${\lambda }_i$对应的特征向量$e_i$,且$\Vert e\Vert =1$

3. 计算主成分贡献率及累计贡献率

对应的单位特征向量$e_i$就是主成分$z_i$关于原变量的系数,即$z_i=x{e}_i^T$

贡献率:

${\alpha }_i=\frac{{\lambda }_i}{{\sum }_{k=1}^p{\lambda }_k}i=1,2,\cdots ,p$

累计贡献率:

$\frac{{\sum }_{k=1}^i{\lambda }_k}{{\sum }_{k=1}^p{\lambda }_k}i=1,2,\cdots ,p$

一般累计贡献率达到85%-95%的特征值${\lambda }_1,{\lambda }_2,..,{\lambda }_m$所对应的第1,2,…,m$(m\le p)$个主成分$z_1,z_2,...,z_m$

4. 计算成分载荷

主成分载荷是反映主成分$z_i$与原变量$x_j$之间的相关关联程度.

$l_{ij}=p\left(z_i,x_j\right)=\sqrt{{\lambda }_i}{e}_{ij}(i,j=1,2,\cdots ,p)$

需要注意的是,在实际应用的时候,指标的量纲往往不同,所以在主成分计算之前应先消除量纲的影响.将变量标准化之后再计算协方差矩阵:

from sklearn.decomposition import PCA
import pandas as pd 
import numpy as np 
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split


data = pd.read_csv("../data/iris.csv",header=None)
data.columns = ['f1','f2','f3','f4','label']

x = data[['f1','f2','f3','f4']].values
y = data['label'].values
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.2)


PCA(n_components=2).fit_transform(x_train)

4.3.2. 线性判别分析法LDA

LDA是一种有监督的降维方法,主要是将高维的样本投影到最佳的控件,其目的是投影后保证模式样本在新的子空间有最大的类间距离和最小的类内距离,即同样的数据点尽可能的接近而不同类的数据点尽可能的分开.

LDA和PCA的区别:

1. LDA有监督,PCA无监督
2. LDA降维最多降维到$k-1$,而PCA没有限制.
3. LDA选择分类性能最好的投影方向,而PCA选择样本点投影具有最大方差的方向.换句话说PCA是为了让映射后的样本发散性最大,而LDA是为了分类性能最好.

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA

import pandas as pd 
import numpy as np 
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split


data = pd.read_csv("../data/iris.csv",header=None)
data.columns = ['f1','f2','f3','f4','label']

x = data[['f1','f2','f3','f4']].values
y = data['label'].values
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.2)


LDA(n_components=2).fit_transform(x_train,y_train)

4.3.3. 局部线性嵌入 LLE

强大的PCA降维算法适用于线性降维,非线性降维方法包括Kernel PCA \ LLE 等, 这次介绍LLE.

4.3.3.1. 流形学习

流形学习是基于流形的思想，其认为现实世界中的高维数据集都可以用低维的流形所代替，而流形一般指高维空间中的几何结构，如曲线或曲面在高维空间中的推广，其是一个空间而不是面。所以直观上来讲，一个流形好比是一个d维的空间，在一个m维的空间中（m>d）被扭曲之后的结果。

• 创建一个三维流形

import matplotlib as mpl
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import proj3d

from sklearn.datasets import make_swiss_roll

X, t = make_swiss_roll(n_samples=1000, noise=0.2, random_state=42)
axes = [-11.5, 14, -2, 23, -12, 15]

fig = plt.figure(figsize=(6,5))
ax = fig.add_subplot(111,projection='3d')

ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=t, cmap=plt.cm.hot)
# ax.view_init(10, -70)
ax.set_xlabel("$x_1$", fontsize=18)
ax.set_ylabel("$x_2$", fontsize=18)
ax.set_zlabel("$x_3$", fontsize=18)
# ax.set_xlim(axes[0:2])
# ax.set_ylim(axes[2:4])
# ax.set_zlim(axes[4:6])
plt.show()

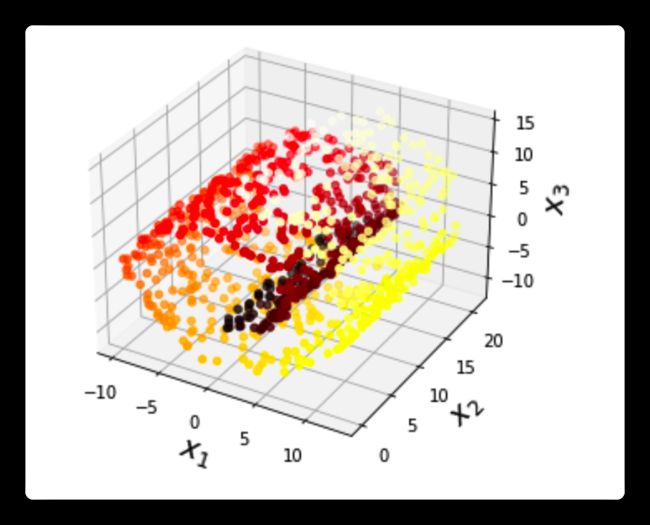
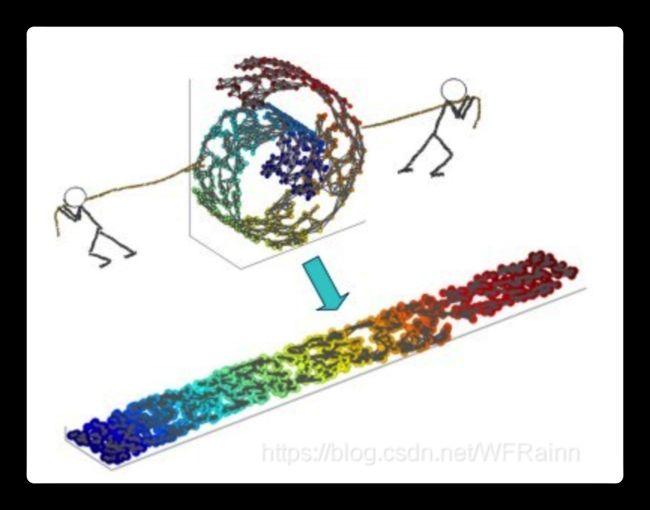
可以看到，虽然数据集是在三维空间中的，但是我们完全可以通过一定的方法将其平铺在二维空间中并同时保存其数据结构。最简单的方法就是将卷曲的带状数据集拉直，如下图：

而这时如果想通过PCA将数据进行降维，效果将会非常差，因为你很难能够找到一个线性的平面将数据很好的进行投影，我们可以通过以下代码对比两种方法：

plt.subplot(121)
plt.scatter(X[:, 0], X[:, 1], c=t, cmap=plt.cm.hot)
plt.axis(axes[:4])
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$x_2$", fontsize=18, rotation=0)
plt.grid(True)

plt.subplot(122)
plt.scatter(t, X[:, 1], c=t, cmap=plt.cm.hot)
plt.axis([4, 15, axes[2], axes[3]])
plt.xlabel("$z_1$", fontsize=18)
plt.grid(True)
plt.show()

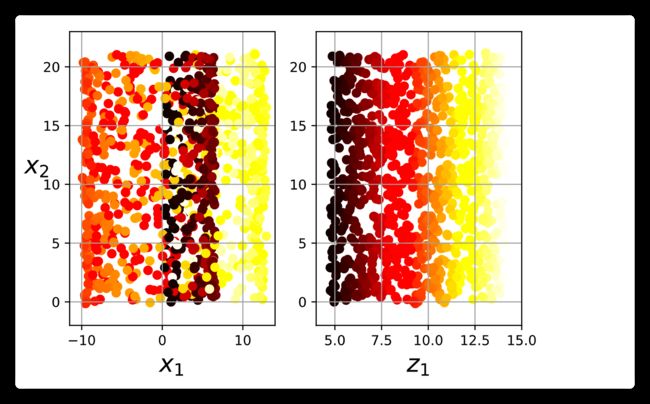
左边是将数据投影在xy平面上的结果，而右边是按照上图所示拉直数据集得到的结果。可以看到右边的降维效果远远好于左边。
基于流形与流形学习的思想，我们可以对数据进行非线性的降维，常见的方法有局部线性嵌入，拉普拉斯特征映射，局部保持投影，等距映射等。

4.3.3.2. LLE

局部线性嵌入算法认为每个数据点可以由其紧邻点的线性加权组合构造得到.

步骤:

1. 寻找每个样本点的k个近邻样本点,
2. 有每个样本点的近邻点计算出该样本点的局部重建权值矩阵,
3. 由权值矩阵计算得到输出

X, t = make_swiss_roll(n_samples=1000, noise=0.2, random_state=41)


from sklearn.manifold import LocallyLinearEmbedding

lle = LocallyLinearEmbedding(n_components=2, n_neighbors=10, random_state=42)
X_reduced = lle.fit_transform(X)
plt.title("Unrolled swiss roll using LLE", fontsize=14)
plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=t, cmap=plt.cm.hot)
plt.xlabel("$z_1$", fontsize=18)
plt.ylabel("$z_2$", fontsize=18)
plt.axis([-0.065, 0.055, -0.1, 0.12])
plt.grid(True)

# plt.save_fig("lle_unrolling_plot")
plt.show()

LLE的实现是基于流形的假设，如果数据集的分布并非流形，则其算法的降维效果可能并不会很出色。在实际运用中，我们可以首先使用原数据集进行机器学习的建模，再通过sklearn包中的GridSearchCV遍历不同的降维算法，查看模型的效果。

4.4. 特征构造

特征构造需要重项目实践中得到.例如客户关系管理中: 最近一次消费间隔时长,消费频率,消费金额就是重要的特征.

5. 过拟合 欠拟合 与正则化

过拟合是烂大街的词汇了. 一张图表明:

欠拟合是指模型不能在训练集上获得足够低的训练误差,往往是由于特征维度过少,导致拟合的函数无法满足训练集,导致误差较大.

过拟合值模型的训练误差与测试误差之间的差距过大,在训练集上表现良好,在测试集上表现过差.

5.1. 解决欠拟合的方法

1. 加入新的特征,对于深度学习,可以利用因子分解机 子编码器等
2. 增加模型复杂度,对于线性模型来讲可以增加高次项,对于深度学习来说可以增加网络层数,神经元个数
3. 减小正则化项的系数,从而提高模型的学习能力.

5.2. 防止过拟合的方法

5.2.1. 正则化

• L1 正则化

L1正则化的目的是减小参数的绝对值总和:

$\Vert x{\Vert }_1={\sum }_i\left|x_i\right|$

• L2 正则化

L2正则化的目的是减少参数平方和的总和

$\Vert x{\Vert }_2={\sum }_i{x}_i^2$

• L1 L2混合正则化

调节L1与L2正则化$\alpha \Vert x{\Vert }_1+\frac{1-\alpha }{2}\Vert x{\Vert }_2$

L1正则化的最优参数的值很大概率会出现在坐标轴上,这样就会导致某一维的权重为0,产生系数权重矩阵.

L2的最优参数值很小概率会出现在坐标轴上,因此每一维的参数都不会是0.

所以,L1常用于特征选择的设置中,而机器学习中最常用的正则化方法是对权重施加L2范数约束.

5.2.2. L2正则化减小过拟合实例

1. 构造数据

import numpy as np 
import pandas as pd 
import random

import matplotlib.pyplot as plt 

from matplotlib.pylab import rcParams

rcParams['figure.figsize'] = 12, 10


x = np.array([1.4*i*np.pi/180 for i in range(0,300,4)])
np.random.seed(20)  #随机数
y = np.sin(x) + np.random.normal(0,0.2,len(x))  # 加噪音
data = pd.DataFrame(np.column_stack([x,y]),columns=['x','y'])
plt.plot(data['x'],data['y'],'.')

2. 训练模型,并对比结果

# 模型复杂度设置
for i in range(2,36):  
    colname = 'x_%d'%i      # 变量名变为 x_i形式
    data[colname] = data['x']**i
    print(data.head()) # 显示五行

# 模型复杂度可变
from sklearn.linear_model import LinearRegression
def linear_regression(data, power, models_to_plot):
    # 初始化预测器
    predictors=['x']
    if power>=2:
        predictors.extend(['x_%d'%i for i in range(2,power+1)])

    # 模型训练
    # linreg = LinearRegression(normalize=True)
    linreg = LinearRegression(normalize=False)
    linreg.fit(data[predictors],data['y'])

    # 预测
    y_pred = linreg.predict(data[predictors])

    # 是否要画图（复杂度是否在models_to_plot中）为了便于比较选择性画图
    if power in models_to_plot:
        plt.subplot(models_to_plot[power])
        plt.tight_layout()
        plt.plot(data['x'],y_pred)
        plt.plot(data['x'],data['y'],'.')
        plt.title('Plot for power: %d'%power)

    # 返回结果
    rss = sum((y_pred-data['y'])**2)
    ret = [rss]
    ret.extend([linreg.intercept_])
    ret.extend(linreg.coef_)
    return ret

col = ['rss','intercept'] + ['coef_x_%d'%i for i in range(1,33)]
ind = ['model_pow_%d'%i for i in range(1,33)]
coef_matrix_simple = pd.DataFrame(index=ind, columns=col)

# 定义作图的位置与模型的复杂度
models_to_plot = {1:331,3:332,6:333,8:334,11:335,14:336,22:337,28:338,32:339}

# 画图
for i in range(1,33):
    coef_matrix_simple.iloc[i-1,0:i+2] = linear_regression(data, power=i, models_to_plot=models_to_plot)

结果如下:

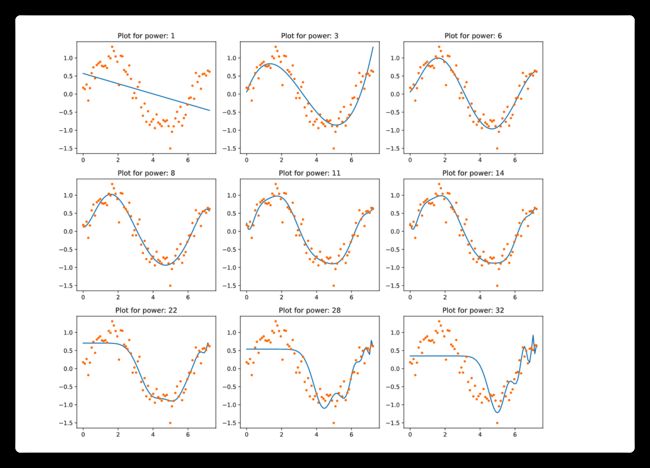
可以看到, 在模型建模过于复杂($x^{2}8x^{3}2$)的时候,模型已经明显不适用了. 我们再来看看加入正则化之后:

# 模型复杂度可变
from sklearn.linear_model import LinearRegression
def linear_regression(data, power, models_to_plot):
    # 初始化预测器
    predictors=['x']
    if power>=2:
        predictors.extend(['x_%d'%i for i in range(2,power+1)])

    # 模型训练
    # linreg = LinearRegression(normalize=True)
    linreg = LinearRegression(normalize=True)
    linreg.fit(data[predictors],data['y'])

    # 预测
    y_pred = linreg.predict(data[predictors])

    # 是否要画图（复杂度是否在models_to_plot中）为了便于比较选择性画图
    if power in models_to_plot:
        plt.subplot(models_to_plot[power])
        plt.tight_layout()
        plt.plot(data['x'],y_pred)
        plt.plot(data['x'],data['y'],'.')
        plt.title('Plot for power: %d'%power)

    # 返回结果
    rss = sum((y_pred-data['y'])**2)
    ret = [rss]
    ret.extend([linreg.intercept_])
    ret.extend(linreg.coef_)
    return ret

col = ['rss','intercept'] + ['coef_x_%d'%i for i in range(1,33)]
ind = ['model_pow_%d'%i for i in range(1,33)]
coef_matrix_simple = pd.DataFrame(index=ind, columns=col)

# 定义作图的位置与模型的复杂度
models_to_plot = {1:331,3:332,6:333,8:334,11:335,14:336,22:337,28:338,32:339}

# 画图
for i in range(1,33):
    coef_matrix_simple.iloc[i-1,0:i+2] = linear_regression(data, power=i, models_to_plot=models_to_plot)

再看看结果:

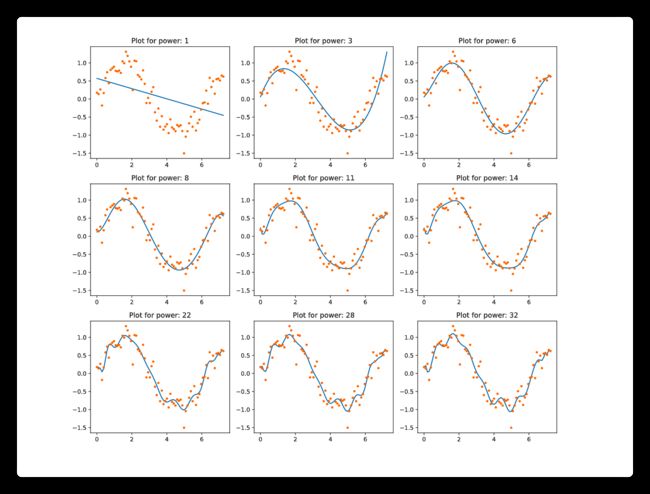
可以发现,在同样复杂度的模型下,模型相对要优秀的多. 这就是正则化在减小模型过拟合中的作用.

5.2.3. L1与L2的区别

• 先验假设

L1对权重$w$的先验假设是拉普拉斯分布,由最大后验概率估计导出.
L2的先验假设是高斯分布.由最大后验概率估计导出.

• 最大后验概率

$MAP=\log P(y\mid X,w)P(w)=\log P(y\mid X,w)+\log P(w)$

P(w)的意义是对权重系数w的概率分布的先验假设，在收集到训练样本后，则可根据{X,y}下的后验概率对w进行修正，从而做出对w的更好地估计。

1. L2
   假设权重$\omega$的先验分布为0均值的高斯分布,即:

$$w_j\sim N\left(0,{\sigma }^2\right)$$

则有:

$$\log P(w)=\log \prod _{j}p\left(w_j\right)=\log \prod _j\left[\frac{1}{\sqrt{2\pi }\sigma }{\mathrm{e}}^{-\frac{w_j^2}{2{\sigma }^2}}\right]=\frac{1}{-2{\sigma }^2}\sum _j{w}_j^2+C$$

可以看到,此时$logP(\omega )$的效果等价于在代价函数中增加L2正则项.

2. L1

假设权重$\omega$的先验分布是均值为0,参数为a的拉普拉斯分布,即:

$P\left(w_j\right)=\frac{1}{\sqrt{2a}}{\mathrm{e}}^{-\frac{|w_j|}{a}}$

则有:

$\log P(w)=\log {\prod }_{j}p\left(w_j\right)=\log {\prod }_j\left[\frac{1}{\sqrt{2a}}{\mathrm{e}}^{-\frac{|w_j|}{a}}\right]=-\frac{1}{a}{\sum }_j\left|w_j\right|+C$

可以看到,此时$logP(\omega )$的效果等价于在代价函数中增加L1正则项.

5.2.4. Batch Normalization

• 缓解梯度消失,加速网络训练,防止过拟合
• Batch Normalization会针对每一批数据在网络的每一层输入之前增加归一化处理，归一代的目的是为了使输入均值为0，标准差为1。

这样能将数据限制在统一的分布下。利用公式表示就是针对每层的第k个神经元，计算这一批数据在第k个神经元的均值与标准差，然后将归一化后的值作为该神经元的激活值

${\hat{x}}_k=\frac{x_k-E\left[x_k\right]}{\sqrt{\mathrm{var}\left[x_k+\epsilon \right]}}$

Batch Normalization通过对数据分布进行额外的约束增强模型的泛化能力，同时由于破坏了之前学到的特征分布，从而也降低了模型的拟合能力。所以为了重构还原最优的输入数据分布:

$$y_k=BN\left(x_k\right)=\gamma {\hat{x}}_k+\beta =\gamma \frac{x_k-E\left[x_k\right]}{\sqrt{\mathrm{var}\left[x_k\right]+\epsilon }}+\beta$$

其中$\gamma$和$\beta$为可训练参数

5.3. Dropout

Dropout 可以避免过拟合,Dropout并不会改变损失函数而是修改网络结构本身。通过对神经网络中的神经元做随机删减，从而降低了网络的复杂度。Dropout在训练大型深度神经网络时非常有用。

运用dropout相当于训练了非常多个仅有部分隐层单元的神经网络，每个这种神经网络，都能够给出一个分类结果，这些结果有的是正确的，有的是错误的。随着训练的进行，大部分网络都能够给出正确的分类结果。

5.4. 迭代截断

迭代截断主要是在模型对训练数据集迭代收敛之前停止迭代来防止过拟合。方法就是在训练的过程中，记录到目前为止最好的准确率，当连续n次Epoch没达到最佳准确率时，就可以停止迭代了。n可以根据实际情况取，如100、200等。

5.5. 交叉验证

k-fold交叉验证是把训练样例分成k份，然后进行k次交叉验证过程，每次使用不同的一份样本作为验证集合，其余k-1份样本合并作为训练集合。每个样例会在一次实验中被用作验证样例，在k-1次实验中被用作训练样例。每次实验中，使用上面讨论的交叉验证过程来决定在验证集合上取得最佳性能的迭代次数，并选择恰当的参数。

6. 常用梯度下降法与优化器

机器学习中的大部分问题都是优化问题,而绝大部分优化问题都可以使用梯度下降法处理,其数学原理是函数沿梯度方向具有最大的效率,在优化的时候沿着负梯度的方向去减小函数的值:

• 梯度方向

$$\mathrm{gradf}\left(x_0,x_1,\cdots ,x_n\right)=\left(\frac{\partial f}{\partial x_0},\frac{\partial f}{\partial x_1},\cdots ,\frac{\partial f}{\partial x_n}\right)$$

沿着负梯度方向减小函数值用表达如下:

$x_0=x_0-\alpha \frac{\partial f}{\partial x_0},x_1=x_1-\alpha \frac{\partial f}{\partial x_1},\cdots ,x_n=x_n-\alpha \frac{\partial f}{\partial x_n}$

以上公式就是执行了一次梯度下降,在算法中会重复直到收敛.

所以梯度下降是一种优化算法，通过迭代的方式寻找模型的最优参数；最优参数即指使目标函数达到最小值时的参数。如果目标函数是凸函数，那么梯度下降的解是全局最优解，不过在一般情况下，梯度下降无法保证全局最优。

6.1. 梯度下降法

6.1.1. 随机梯度下降与小批量梯度下降

标准梯度下降法每次都需要对所有训练样本的平均损失来更新参数,相当消耗计算资源. 于是大家常用的是随机梯度下降算法(SGD)或者小批量(batch值为32,46,128等).

随机梯度下降每次只采用单个样本来估计当前的梯度,并不稳定,最常用的是小批量梯度下降法.

6.1.2. 动量算法

动量算法:

$$\begin{array}{c}g\leftarrow \frac{1}{m}{\nabla }_{\theta }\sum _{i}L\left(f\left(x_i;\theta \right),y_i\right)\\ v_t=a{v}_{t-1}-\epsilon g_t\\ {\theta }_{t+1}={\theta }_t+v_t\end{array}$$

动量算法引入了变量v充当速度角色,以及相关的超参数$\alpha$,其一般取0.5,0.9,0.99分别对应最大2倍,最大10倍和100倍的步长.

动量算法可以用来解决鞍点问题;也可以用于SGD加速,特别是针对高区率,小幅但是方向一致的梯度对象. 动量方法的训练过程更加稳定,同时在鞍点处因为惯性的作用,更因可能离开平缓的梯度部分.

随机梯度下降法每次更新的步长只是梯度乘以学习略,而动量算法的步长还取决于历史梯度序列的大小和排序,当若干连续的梯度方向相同时,步长会被不断增大.

6.1.3. NAG算法(Nesterov动量)

NAG是对参数施加当前速度后才进行梯度计算的,这个设计让算法有了对前方环境的预判能力,换句话讲,NAG算法相当于在标准动量方法中添加了一个修正因子,并且在计算参数的梯度时,在损失函数中减去了动量项.

$$\begin{array}{c}\hat{\theta }=\theta +av\\ g\leftarrow \frac{1}{m}{\nabla }_{\hat{\theta }}\sum _{i}L\left(f\left(x_i;\hat{\theta }\right),y_i\right)\\ v_t=a{v}_{t-1}-\epsilon g_t\\ {\theta }_{t+1}={\theta }_t+v_t\end{array}$$

6.1.4. 自适应学习率算法

学习率决定了参数空间搜索的步长,所以非常岁要,但也比较难设置.

6.1.4.1. AdaGrad

• 设定一个全局学习率$\epsilon$

$${\epsilon }_n=\frac{\epsilon }{\delta +\sqrt{{\sum }_{j=1}^{n-1}{g}_i\odot g_i}}$$

• 步骤

1. 预先设定 全局学习率$\epsilon$,初试参数$\theta$,数值稳定量$\delta$
2. 中间变量: 梯度累积值$r$
3. 迭代过程:
   $$\begin{array}{c}\tilde{g}\leftarrow \frac{1}{m}{\nabla }_{\theta }\sum _{i}L\left(f\left(x_i;\theta \right),y_i\right)\\ r\leftarrow r+\tilde{g}\odot \tilde{g}\\ \theta \leftarrow \theta -\frac{\epsilon }{\delta +\sqrt{r}}\odot \tilde{g}\end{array}$$

AdaGard更新参数的过程如下:

$$w_{t+1}\leftarrow w_t-\frac{\eta }{\sqrt{{\sum }_{t=0}^t{\left(g_i\right)}^2}}{g}_t$$

其中,KaTeX parse error: Undefined control sequence: \g at position 1: \̲g̲_t为参数的梯度.

6.1.4.2. RMSProp

RMSProp是AdaGrad算法的升级版,在非凸优化问题上表现很好,因为它使用指数衰减来处理历史信息,可以使得模型在找到凸结构后幻速收敛. RMSProp与AdaGrad的区别在于用来控制历史信息获取的衰减系数,算法的具体步骤如下:

• 预设定: 全局学习率 $\epsilon$ ,初试参数$\theta$ , 数值稳定量$\delta$, 衰减系数$\rho$
• 中间变量: 梯度累积量$r$

迭代公式:

$$\begin{array}{rl}\tilde{g}\leftarrow & \frac{1}{m}{\nabla }_{\theta }\sum _{i}L\left(f\left(x_i;\theta \right),y_i\right)\\ r\leftarrow \rho r+(1-\rho )\tilde{g}\odot \tilde{g}& \\ & \theta \leftarrow \theta -\frac{\epsilon }{\delta +\sqrt{r}}\odot \tilde{g}\end{array}$$

RMSProp可以解决AdaGrad在多隐层网络中过早结束训练的缺点,适合处理非平稳的目标,但同时也引入了新的超参数衰减系数,并且依旧依赖于全局学习率.

6.1.4.3. Adam

Adam(Adaptive Moment Estimation) 是常见的深度学习训练时使用的优化器. 相比于AdaGrad算法,Adam能让每次迭代的学习率处在一定范围内,因而比较稳定.

算法的具体过程:

• 需要预先设定的值:

  1. 步长因子$\epsilon$
  2. 初始参数$\theta$
  3. 数值稳定量$\delta$
  4. 一阶动量衰减系数${\rho }_1$
  5. 二阶动量衰减系数${\rho }_2$

(默认:$\epsilon =0.001,\delta =10^{-8},{\rho }_1=0.9,{\rho }_2=0.999$)

• 中间变量

  1. 一阶动量$s$
  2. 二阶动量$r$

• 迭代过程
  $$\begin{array}{c}\tilde{g}\leftarrow \frac{1}{m}{\nabla }_{\theta }\sum _{i}L\left(f\left(x_i;\theta \right),y_i\right)\\ s\leftarrow {\rho }_{1}s+(1-\rho )\tilde{g}\\ r\leftarrow {\rho }_{2}r+\left(1-{\rho }_2\right)\tilde{g}\odot \tilde{g}\\ \theta \leftarrow \theta -\epsilon \frac{\frac{S}{1-{\rho }_1}}{\delta +\sqrt{\frac{r}{1-{\rho }_2}}}\odot \tilde{g}\end{array}$$

优化算法的选择并没有绝对的原则,没有哪个算法具有绝对优势,应该根据具体任务来选择. 事实上在面对具体问题的时候可以将Adam和RMSProp都训练一次,比较结果差距,在选择恰当的优化器.

6.2. 比较牛顿法与梯度下降法

6.2.1. 牛顿法的基本思想

• 极小点估计值$x_K$,对$f(x)$做二阶泰勒展开,从该点的附件找到极值点的下一个估计值. 这里设$x_K$为当前的估计值,那么$f(x)$在$x_k$附件的二阶泰勒展开式为:

$$\phi (x)=f\left(x_k\right)+f^{\prime }\left(x_k\right)\left(x-x_k\right)+\frac{1}{2}{f}^{\prime \prime }\left(x_k\right){\left(x-x_k\right)}^2$$

由于求得是最值,由极值的必要条件可知,$\varphi (x)$应该满足KaTeX parse error: Expected group after '^' at position 5: \phi^̲'(x)=0,即

$$f^{\prime }\left(x_k\right)+f^{\prime \prime }\left(x_k\right)\left(x-x_k\right)=0$$

从而求得:

$$x=x_k-\frac{f^{\prime }\left(x_k\right)}{f^{\prime \prime }\left(x_k\right)}$$

于是,给定初始值$x_0$,就可以得到如下迭代式:

$$x_{k+1}=x_k-\frac{f^{\prime }\left(x_k\right)}{f^{\prime \prime }\left(x_k\right)}k=0,1,\cdots$$

迭代式中的$d_k=-H_k^{-1}\cdot g_k$成为牛顿方向,下面给出完整的牛顿迭代算法:

1. 给定初值$x_0$和精度的阈值$\epsilon$,并令$K=0$
2. 计算$g_k$和$H_k$
3. 若$\Vert g_k\Vert <\epsilon$,则停止迭代,否则确定搜索方向$d_k=-H_k^{-1}\cdot g_k$
4. 计算新的迭代点$X_{k+1}=X_k+d_k$
5. 令$k=k+1$,转到步骤2

6.2.2. 两者比较

由上可得梯度下降法与牛顿下降法最大区别是梯度下降法使用的梯度信息是一阶导数，而牛顿法除了一阶导数外，还会使用二阶导数的信息。

牛顿法的优点是收敛速度快，能用更少的迭代次数找到最优解，缺点是每一步都需要求解目标函数的Hessian矩阵的逆矩阵，计算量非常大。

7. 其他问题

7.1. 常见的损失函数

7.1.1. 0-1 loss

直接记录分类错误的次数

7.1.2. Hinge Loss

最常用在SVM的最大间隔分类中,对可能的输出$t=\pm 1$和分类器分数$y$,预测值y的hinge loss定义如下:

$L(y)=\max (0.1-t\ast y)$

7.1.3. Log Loss

对于对数函数，由于其具有单调性，在求最优化问题时，结果与原始目标一致，在含有乘积的目标函数中（如极大似然函数），通过取对数可以转化为求和的形式，从而大大简化目标函数的求解过程

7.1.4. Squared Loss 平方损失

即真实值与预测值之差的平方和。通常用于线性模型中，如线性回归模型。

7.1.5. Exponential Loss 指数损失

指数函数的特点是越接近正确结果误差越小，Adaboost算法即使用的指数损失目标函数。但是指数损失存在的一个问题是误分类样本的权重会指数上升，如果数据样本是异常点，会极大地干扰后面基本分类器学习效果。

7.2. 如何判断函数凸或非凸

首先定义凸集,如果x,y属于某个集合M,并且所有的$\theta x+(1-\theta )y$也属于M,那么M为一个凸集. 如果函数$f$的定义域是凸集,并且满足:

$f(\theta x+(1-\theta )y)⩽\theta f(x)+(1-\theta )f(y)$

则该函数为凸函数. 上述条件还能推出更普适的结果.

$f\left({\sum }_{i=1}^k{\theta }_i{x}_i\right)⩽{\sum }_{i=1}^k{\theta }_{i}f\left(x_i\right)$
${\sum }_{i=1}^k{\theta }_i=1,{\theta }_i⩾0$

如果函数存在二阶导数且为正，或者多元函数的Hessian矩阵半正定则均为凸函数

7.3. 数据不平衡问题应该如何解决

• 正负样本的数量差距很大

解决方案包括:

7.3.1. 数据采样

数据采样分为上采样和下采样。上采样是将少量数据类别的数据重复复制使得各类别的比例维持在正常水平，不过这种方法容易导致过拟合，所以需要在生成新数据的时候加入较小的随机扰动。下采样则相反，从多数数据类中筛选出一部分从而使各类别数据比例维持在正常水平，但是容易丢失比较重要的信息，所以需要多次随机下采样。

7.3.2. 数据合成

数据合成是利用已有样本的特征相似性生成更多新的样本。

7.3.3. 加权

加权是通过对不同类别分类错误施加不同权重的代价，使得机器学习时更侧重样本较少且容易出错的样本。

7.3.4. 一分类

当正负样本比例严重失衡时，采样和数据合成会导致原始数据的真实分布产生变化太大，从而导致模型训练结果并不能真正反映实际的情况，训练时会产生很大的偏差。那么此时可以用一分类的方法解决。例如One-class SVM，该算法利用高斯核函数将样本空间映射到核空间，在核空间中找到一个包含所有数据的高维球体。如果测试数据位于这个高维球体之中，则归为多数类，否则就归为少数类。

7.4. 熵相关定义

在物理学中,熵表示一个热力系统的无序程度

$\Delta S=\frac{Q}{T}$

其中Q是吸收或者释放的热量,T是温度

计算机领域将其定义为离散随机事件的出现概率。一个系统越是有序，信息熵就越低；反之，系统越是混乱，信息熵就越高。所以信息熵用来衡量系统有序化程度。

如果一个随机变量X的可能取值为$X=\left\{x_1,x_2,\dots ,x_k\right\}$,概率分布为$P\left(X=x_i\right)=p_i(i=1,2,\dots ,n)$,则随机变量X的熵定义为

$\begin{array}{rl}H(X)& =-\sum _{x}p(x)\log p(x)\\ & =\sum _{x}p(x)\log \frac{1}{p(x)}\end{array}$

• 联合熵,两个随机变量X,Y的联合分布可求得联合熵:

$H(X,Y)=-{\sum }_{x}p(x,y)\log p(x,y)$

• 条件熵,在随机变量X发生的前提下，随机变量Y带来的新的熵即为Y的条件熵：

$H(X\mid Y)=-{\sum }_{x,y}p(x,y)\log p(y\mid x)$

其含义是衡量在已知随机变量X的条件下随机变量Y的不确定性。

• 推论$H(YX)=H(X,Y)-H(X)$

$$\begin{array}{rl}H(X,Y)-H(X)& =-\sum _{x}p(x,y)\log p(x,y)+\sum _{x}p(x)\log p(x)\\ & =-\sum _{x,y}p(x,y)\log p(x,y)+\sum _{x,y}p(x,y)\log p(x)\\ & =-\sum _{x,y}p(x,y)\log \frac{p(x,y)}{p(x)}\\ & =-\sum p(x,y)\log p(x\mid y)\end{array}$$

• KL散度:

设$f(x),g(x)$是X中取值的两个概率分布,则$f$对$g$的KL散度是:

$D(f\Vert g)=-{\sum }_{x}f(x)\log \frac{f(x)}{g(x)}=E_{f(x)}\log \frac{f(x)}{g(x)}$

• 互信息

两个随机变量X，Y的互信息定义为X，Y的联合分布和各自独立分布乘积的KL散度
$I(X,Y)={\sum }_{x,y}f(x,y)\log \frac{f(x,y)}{f(x)f(y)}$

在定义完KL散度和互信息后，即得：H(Y)-I(X,Y)=H(Y|X)，推导如下：

$\begin{array}{rl}H(Y)-I(X,Y)& =-\sum _{y}f(x)\log f(y)-\sum _{x,y}f(x,y)\log \frac{f(x,y)}{f(x)f(y)}\\ & =-\sum _y\left(\sum _{x}f(x,y)\right)\log f(x)-\sum _{x,y}f(x,y)\log \frac{f(x,y)}{f(x)f(y)}\\ & =-\sum _{x}f(x,y)\log f(x)-\sum _{x,y}f(x,y)\log \frac{f(x,y)}{f(x)f(y)}\\ & =-\sum f(x,y)\log f(y\mid x)=H(Y\mid X)\end{array}$

用韦恩图表示，如图2-3所示，互信息I(X,Y)表示在Y给定下X的混乱程度的减少量，或Y给定下X的混乱程度的减少量。也就是Y或X信息增益。

图2-3中H(X,Y)表示联合熵，满足H(X,Y)=H(X)+H(Y|X)。另外可以看到，虽然信息增益互信息有等价关系，但熵与互信息的角度不同，前者侧重一个特征对象，后者侧重两两对象的关系。

7.5. 主成分分析与因子分析的区别

在做数据挖掘时，变量之间信息的高度重叠和高度相关会给结果分析带来许多障碍。所以需要在削减变量的个数的同时尽可能避免信息丢失和信息不完整。

主成分分析的具体算法步骤已经在“特征工程”一节中展示过，其基本思想是将具有一定相关性的指标$x_1,x_2,\dots ,x_p$，重新组合成一组个数较少的互不相关的综合新指标。新指标应该既能最大程度反映原变量所代表的信息，又能保证新指标之间保持相互无关。

因子分析的基本思想是根据相关性大小把原始变量分组，使得同组内的变量之间相关性较高，而不同组的变量间的相关性则较低.原始变量进行分解后会得到公共因子和特殊因子。公共因子是原始变量中共同具有的特征，而特殊因子则是原始变量所特有的部分。

它们之间的区别如下:

1）主成分分析是从空间生成的角度寻找能解释诸多变量变异绝大部分的几组彼此不相关的主成分。而因子分析是寻找对变量起解释作用的公共因子和特殊因子，以及公共因子和特殊因子组合系数。

2）因子分析把变量表示成各因子的线性组合，而主成分分析中则把主成分表示成了各变量的线性组合。

3）主成分分析中不需要假设，因子分析有一些假设，例如公共因子和特殊因子之间不相关等。

4）主成分分析中，由于给定的协方差矩阵或者相关矩阵的特征值是唯一的，所以主成分一般是固定的；而因子分析可以通过旋转得到不同的因子。

7.6. 什么是最小风险贝叶斯决策

贝叶斯定理会根据一件事发生的先验知识计算出它的后验概率。数学上，它表示为：一个条件样本发生的真正率占真正率和假正率之和的比例，即：

$P(A\mid B)=\frac{P(B\mid A)P(A)}{P(B)}$

最小风险贝叶斯决策的算法步骤描述如下:

1. 在已知$P({\omega }_i)，P(X|{\omega }_i)，i=1,\dots ,c$及给出待识别的$X$的情况下，计算后验概率$P(X|\omega$i)$。

2. 利用计算出的后验概率及决策表,按下面的公式计算出采取$a_j$的条件风险

$R\left(a_i\mid X\right)={\sum }_{j=1}^c\lambda \left(a_i,{\omega }_j\right)P\left({\omega }_j\mid X\right)$

3. 对上面计算得到的a个条件风险值R(ai|X)进行比较，找出使其条件风险最小的决策ak，即$R\left(a_k\mid x\right)={\min }_{i=1,\cdots ,a}R\left(a_i\mid x\right)$

此时则将$a_k$称为最小风险贝叶斯决策.

7.7. 什么是贝叶斯最小错误概率和最小风险

例如,有一种病症,正常率为$p({\omega }_1)=0.9$,发病率为$p({\omega }_2)=0.1$ ,某人的检查结果为x,由概率曲线查出:

$P\left(x\mid {\omega }_1\right)=0.2,P\left(x\mid {\omega }_2\right)=0.4$

风险代价矩阵为:

$$L=\left[\begin{array}{ll}{L}_{11}& L_{12}\\ L_{21}& L_{22}\end{array}\right]=\left[\begin{array}{ll}0& 6\\ 1& 0\end{array}\right]$$

下面分别通过计算贝叶斯最小错误概率和贝叶斯最小风险的方式判别$x$是${\omega }_1$还是${\omega }_2$

基于最小错误率的贝叶斯决策是利用概率论中的贝叶斯公式，得出使得错误率最小的分类规则。而基于最小风险的贝叶斯决策，引入了损失函数，得出使决策风险最小的分类。当在0-1损失函数条件下，基于最小风险的贝叶斯决策变成基于最小错误率的贝叶斯决策。

用贝叶斯最小错误概率计算如下:

$$\begin{array}{rl}& P\left({\omega }_1\mid x\right)\propto P\left({\omega }_1\right)P\left(x\mid {\omega }_2\right)\\ & P\left({\omega }_2\mid x\right)\propto P\left({\omega }_2\right)P\left(x\mid {\omega }_2\right)\end{array}$$

由于:

$$l=\frac{P\left(x\mid {\omega }_1\right)}{P\left(x\mid {\omega }_2\right)}=\frac{1}{2}>\frac{P\left({\omega }_2\right)}{P\left({\omega }_1\right)}=\frac{1}{9}$$

所以,$x\in {\omega }_1$

用于计算贝叶斯最小风险的方式:

$r_j(x)={\sum }_{i=1}^2{L}_{ij}P\left(x\mid {\omega }_i\right)P\left({\omega }_i\right),j=1,2$

由于:

$$l^{\prime }=\frac{P\left(x\mid {\omega }_1\right)}{P\left(x\mid {\omega }_2\right)}=\frac{1}{2}>\frac{P\left({\omega }_2\right)}{P\left({\omega }_1\right)}\frac{L_{21}-L_{22}}{L_{12}-L_{11}}=\frac{1}{54}$$

所以$x\in {\omega }_1$

.

8. 结语

先不要什么结语,因为很多地方还没有写实现代码.后续会在这个基础上更新的. 祝好!