【机器学习基础】样本类别不平衡的解决办法

目录

一 数据不平衡现象以及分析

二 解决措施

1.采样

（1）随机下采样（Random undersampling of majority class）

（2）随机过采样

（3）Edited Nearest Neighbor算法

（4）Repeated Edited Nearest Neighbor算法

（5）EasyEnsemble算法

         （6）BalanceCascade算法

（7）NearMiss算法

（8）Tomek Link算法

2.数据合成

（1）SMOTE算法

（2）Borderline-SMOTE算法

（3）ADASYN算法

三 参考资料

---

一 数据不平衡现象以及分析

    在进行一些分类的任务时，很多算法模型都有一个假设是数据的分布是均匀的，在数据分布均匀的前提下，模型才能发挥出更好的效果，但是在我们实际的应用场景中，我们的数据往往达不到这样理想的情况，特别是在多分类任务中，不同类别之间的差距很有可能就比较大，而且很多情况下都会存在“长尾现象”，比如下图给的一个例子：

    可以看到对于上述例子，有的类别样本量达到了4K，有的却是个位数，当然这个取决于问题本身，其实对于大部分的数据集来说，都会存在样本不平衡的问题，但是就看这个不平衡的影响程度，也有可能相同的不平衡比例下，不同数据集大小的影响程度也不同。很简单的举个例子，有A,B两个类别，一个数据集A和B分别有1000万和50万条数据，另一个数据集A和B只有1万和500条数据，很明显后者是很难训练出好的模型。由于针对不同的实际问题具体的数据处理方式都会有所不同，本文只讨论一些公共的针对数据不平衡问题的解决办法。

二 解决措施

1.采样

    采样是使得数据集趋向平衡的最简单直接的方式，采样从思想上分成过采样和欠采样，过采样是使得小类别的样本数据量增加，欠采样是减少大类别样本数据量。

 （1）随机下采样（Random undersampling of majority class）

    随机下采样的思想非常简单，就是从数量多的类别中，随机选取一些样本剔除掉，这种方法的弊端也很明显，被剔除的样本可能包含着一些重要信息，致使学习出来的模型效果不好。这个方法在Python的库imblearn.under_sampling-RandomUnderSampler可以直接调用。

（2）随机过采样

    随机过采样就是通过有放回的抽样，不断的从少数类的抽取样本，不过要注意的是这个方法很容易会导致过拟合。、

（3）Edited Nearest Neighbor算法

    对于大类别的样本，如果他的大部分k近邻样本都跟他自己本身的类别不一样，我们就将他删除。

（4）Repeated Edited Nearest Neighbor算法

    一直重复Edited Nearest Neighbor算法直到没有样本需要被删除为止

（5）EasyEnsemble算法

    EasyEnsemble算法是一种有效的不均衡数据分类方法。它将多数类样本随机分成多个子集，每个子集分别与少数类合并，得到多个新的训练子集，并利用每个训练子集训练一个AdaBoost基分类器，最后集成所有基分类器，得到最终的分类器。       

    EasyEnsemble算法有效解决了数据不均衡问题，且减少欠采样造成的多数类样本信息损失。但是，EasyEnsemble算法未考虑少数类样本极度欠缺的情况，由于少数类样本数远小于正确训练分类器所需的样本数，导致基学习器的分类性能差，进而最终的分类器性能也很差。另外，噪声是另一个影响分类器性能的关键因素，在EasyEnsemble算法中并未考虑。

（6）BalanceCascade算法

    BalanceCascade和EasyEnsemble其实大致上是类似的，如果说EasyEnsemble是基于无监督的方式从多数类样本中生成子集进行欠采样，那么BalanceCascade则是采用了有监督结合Boosting的方式。在第n轮训练中，将从多数类样本中抽样得来的子集与少数类样本结合起来训练一个基学习器H，训练完后多数类中能被H正确分类的样本会被剔除。在接下来的第n+1轮中，从被剔除后的多数类样本中产生子集用于与少数类样本结合起来训练，最后将不同的基学习器集成起来。BalanceCascade的有监督表现在每一轮的基学习器起到了在多数类中选择样本的作用，而其Boosting特点则体现在每一轮丢弃被正确分类的样本，进而后续基学习器会更注重那些之前分类错误的样本。

 

（7）NearMiss算法

    NearMiss的思想也是从大类别的样本中抽取一定数量的样本跟小类别样本放到一起进行训练，只不过与随机欠采样不同的就是选择样本的时候有一定的规则性，也是为了缓解一定程度上的信息丢失问题，NearMiss分成以下三类：
    NearMiss-1：采样的规则为选择到最近的K个少数类样本平均距离最近的多数类样本。

    NearMiss-2：采样的规则为选择到最远的K个少数类样本平均距离最近的多数类样本。

    NearMiss-3：对于每个小众样本，选择离它最近的K个大众样本，目的是保证每个小众样本都被大众样本包围。

 

优缺点：
NearMiss-1考虑的是与最近的K个小众样本的平均距离，是局部的，易受离群点的影响；NearMiss-2考虑的是与最远的K个小众样本的平均距离，是全局的。而NearMiss-3方法则会使得每一个小众样本附近都有足够多的大众样本，显然这会使得模型的精确度高、召回率低。有论文中证明了在某些数据下NearMiss-2方法的效果最好。但三种方法的计算量普遍都很大。

（8）Tomek Link算法

    Tomek Link表示不同类别之间距离最近的一对样本，即这两个样本互为最近邻且分属不同类别。这样如果两个样本形成了一个Tomek Link，则要么其中一个是噪音，要么两个样本都在边界附近。这样通过移除Tomek Link就能“清洗掉”类间重叠样本，使得互为最近邻的样本皆属于同一类别，从而能更好地进行分类。

优缺点：
可以减少不同类别之间的样本重叠，但当作为欠采样时，无法控制欠采样的数量，能剔除的大众样本比较有限，故最好作为数据清洗的方法，结合其他方法使用。
实现方法：
Python:imblearn.under_sampling-TomekLinks（ratio='auto’为移除多数类的样本, 当ratio='all’时, 两个样本均被移除。）

2.数据合成

（1）SMOTE算法

    SMOTE的全称是Synthetic Minority Over-Sampling Technique 即“人工少数类过采样法”，非直接对少数类进行重采样，而是设计算法来人工合成一些新的少数样本。

算法流程：
1.对于小众中每一个样本，计算该点与小众中其他样本点的距离，得到最近的k个近邻（即对小众点进行KNN算法）。
2.根据样本不平衡比例设置一个采样比例以确定采样倍率，对于每一个小众样本，从其k近邻中随机选择若干个样本，假设选择的近邻为
3.对于每一个随机选出的近邻，分别与原样本按照如下的公式构建新的样本：

SMOTE算法的缺陷

    该算法主要存在两方面的问题:

• 一是在近邻选择时,存在一定的盲目性。从上面的算法流程可以看出,在算法执行过程中,需要确定K值,即选择多少个近邻样本,这需要用户自行解决。从K值的定义可以看出,K值的下限是M值(M值为从K个近邻中随机挑选出的近邻样本的个数,且有M< K),M的大小可以根据负类样本数量、正类样本数量和数据集最后需要达到的平衡率决定。但K值的上限没有办法确定,只能根据具体的数据集去反复测试。因此如何确定K值,才能使算法达到最优这是未知的。
• 另外,该算法无法克服非平衡数据集的数据分布问题,容易产生分布边缘化问题。由于负类样本的分布决定了其可选择的近邻,如果一个负类样本处在负类样本集的分布边缘,则由此负类样本和相邻样本产生的“人造”样本也会处在这个边缘,且会越来越边缘化,从而模糊了正类样本和负类样本的边界,而且使边界变得越来越模糊。这种边界模糊性,虽然使数据集的平衡性得到了改善,但加大了分类算法进行分类的难度．

针对SMOTE算法的进一步改进

    针对SMOTE算法存在的边缘化和盲目性等问题,很多人纷纷提出了新的改进办法,在一定程度上改进了算法的性能,但还存在许多需要解决的问题。

    Han等人Borderline-SMOTE: A New Over-Sampling Method in Imbalanced Data Sets Learning在SMOTE算法基础上进行了改进,提出了Borderhne.SMOTE算法,解决了生成样本重叠(Overlapping)的问题该算法在运行的过程中,查找一个适当的区域,该区域可以较好地反应数据集的性质,然后在该区域内进行插值,以使新增加的“人造”样本更有效。这个适当的区域一般由经验给定,因此算法在执行的过程中有一定的局限性。

'''
SMOTE参数说明：
imblearn.over_sampling.SMOTE(
sampling_strategy = ‘auto’,
random_state = None, ## 随机器设定
k_neighbors = 5, ## 用相近的 5 个样本（中的一个）生成正样本
m_neighbors = 10, ## 当使用 kind={'borderline1', 'borderline2', 'svm'}
out_step = ‘0.5’, ## 当使用kind = 'svm'
kind = 'regular', ## 随机选取少数类的样本
– borderline1： 最近邻中的随机样本b与该少数类样本a来自于不同的类
– borderline2： 随机样本b可以是属于任何一个类的样本;
– svm：使用支持向量机分类器产生支持向量然后再生成新的少数类样本
svm_estimator = SVC(), ## svm 分类器的选取
n_jobs = 1, ## 使用的例程数，为-1时使用全部CPU
ratio=None
)
'''

from imblearn.over_sampling import SMOTE
sm = SMOTE(random_state = 42, n_jobs = -1)
x, y = sm.fit_sample(x_val, y_val)

 

（2）Borderline-SMOTE算法

    这个是对SMOTE算法的一个改进，SMOTE算法在生成新样本的时候，是对所有的小众样本都考虑进去了，但实际建模过程中发现那些处于边界位置的样本更容易被错分，因此增加的新样本如果是在边界位置附近的话，可以对于模型的分类效果带来更大的提升。

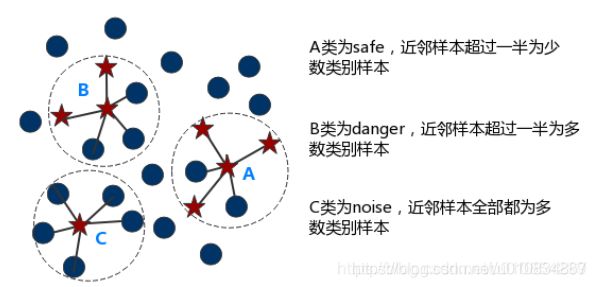
Borderline SMOTE采样过程是将少数类样本分为3类，分别为Safe、Danger和Noise，具体说明如下。最后，仅对表为Danger的少数类样本过采样。
  Safe，样本周围一半以上均为少数类样本，如图中点A
  Danger：样本周围一半以上均为多数类样本，视为在边界上的样本，如图中点B
  Noise：样本周围均为多数类样本，视为噪音，如图中点C
 

    Borderline SMOTE有两个版本：Borderline SMOTE1和Borderline SMOTE2。Borderline SMOTE1在对Danger点生成新样本时，在K近邻随机选择少数类样本（与SMOTE相同），Borderline SMOTE2则是在k近邻中的任意一个样本(不关注样本类别)

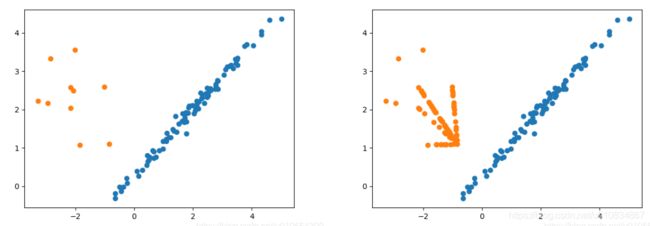
采样前后效果对比：

优缺点：
两种Borderline SMOTE方法都可以加强边界处模糊样本的存在感，且Borderline SMOTE-2又能在此基础上使新增样本更加靠近真实值。
实现方法：
Python：imblearn.over_sampling-SMOTE，kind参数中可选borderline1或borderline2；

下面给出一份包调用样例提供参考

from collections import Counter
from sklearn.datasets import make_classification
from imblearn.over_sampling import BorderlineSMOTE
X, y = make_classification(n_classes=2, class_sep=2,
                           weights=[0.1, 0.9], n_informative=2, n_redundant=0, flip_y=0,
                           n_features=2, n_clusters_per_class=1, n_samples=100, random_state=9)
print('Original dataset shape %s' % Counter(y))
sm = BorderlineSMOTE(random_state=42,kind="borderline-1")
X_res, y_res = sm.fit_resample(X, y)

再给出一份实现代码提供参考：

from sklearn.neighbors import NearestNeighbors
from sklearn.utils import safe_indexing
 
from base_sampler import *
import numpy as np
 
 
# 处于多数类与少数类边缘的样本
def in_danger(imbalanced_featured_data, old_feature_data, old_label_data, imbalanced_label_data):
    nn_m = NearestNeighbors(n_neighbors=11).fit(imbalanced_featured_data)
    # 获取每一个少数类样本点周围最近的n_neighbors-1个点的位置矩阵
    nnm_x = NearestNeighbors(n_neighbors=11).fit(imbalanced_featured_data).kneighbors(old_feature_data,
                                                                                    return_distance=False)[:,1:]
    nn_label = (imbalanced_label_data[nnm_x] != old_label_data).astype(int)
    n_maj = np.sum(nn_label, axis=1)
    return np.bitwise_and(n_maj >= (nn_m.n_neighbors - 1) / 2, n_maj < nn_m.n_neighbors - 1)
 
 
# 产生少数类新样本的方法
def make_sample(imbalanced_data_arr2, diff):
    # 将数据集分开为少数类数据和多数类数据
    minor_data_arr2, major_data_arr2 = seperate_minor_and_major_data(imbalanced_data_arr2)
    imbalanced_featured_data = imbalanced_data_arr2[:, : -1]
    imbalanced_label_data = imbalanced_data_arr2[:, -1]
    # 原始少数样本的特征集
    old_feature_data = minor_data_arr2[:, : -1]
    # 原始少数样本的标签值
    old_label_data = minor_data_arr2[0][-1]
    danger_index = in_danger(imbalanced_featured_data, old_feature_data, old_label_data, imbalanced_label_data)
    # 少数样本中噪音集合，也就是最终要产生新样本的集合
    danger_index_data = safe_indexing(old_feature_data, danger_index)
    # 获取每一个少数类样本点周围最近的n_neighbors-1个点的位置矩阵
    nns = NearestNeighbors(n_neighbors=6).fit(old_feature_data).kneighbors(danger_index_data,
                                                                           return_distance=False)[:, 1:]
    # 随机产生diff个随机数作为之后产生新样本的选取的样本下标值
    samples_indices = np.random.randint(low=0, high=np.shape(danger_index_data)[0], size=diff)
    # 随机产生diff个随机数作为之后产生新样本的间距值
    steps = np.random.uniform(size=diff)
    cols = np.mod(samples_indices, nns.shape[1])
    reshaped_feature = np.zeros((diff, danger_index_data.shape[1]))
    for i, (col, step) in enumerate(zip(cols, steps)):
        row = samples_indices[i]
        reshaped_feature[i] = danger_index_data[row] - step * (danger_index_data[row] - old_feature_data[nns[row, col]])
    new_min_feature_data = np.vstack((reshaped_feature, old_feature_data))
    return new_min_feature_data
 
 
# 对不平衡的数据集imbalanced_data_arr2进行Border-SMOTE采样操作，返回平衡数据集
# :param imbalanced_data_arr2: 非平衡数据集
# :return: 平衡后的数据集
def Border_SMOTE(imbalanced_data_arr2):
    # 将数据集分开为少数类数据和多数类数据
    minor_data_arr2, major_data_arr2 = seperate_minor_and_major_data(imbalanced_data_arr2)
    # print(minor_data_arr2.shape)
    # 计算多数类数据和少数类数据之间的数量差,也是需要过采样的数量
    diff = major_data_arr2.shape[0] - minor_data_arr2.shape[0]
    # 原始少数样本的标签值
    old_label_data = minor_data_arr2[0][-1]
    # 使用K近邻方法产生的新样本特征集
    new_feature_data = make_sample(imbalanced_data_arr2, diff)
    # 使用K近邻方法产生的新样本标签数组
    new_labels_data = np.array([old_label_data] * np.shape(major_data_arr2)[0])
    # 将类别标签数组合并到少数类样本特征集，构建出新的少数类样本数据集
    new_minor_data_arr2 = np.column_stack((new_feature_data, new_labels_data))
    # print(new_minor_data_arr2[:,-1])
    # 将少数类数据集和多数据类数据集合并，并对样本数据进行打乱重排，
    balanced_data_arr2 = concat_and_shuffle_data(new_minor_data_arr2, major_data_arr2)
    return balanced_data_arr2
 
 
# 测试
if __name__ == '__main__':
    imbalanced_data = np.load('imbalanced_train_data_arr2.npy')
    print(imbalanced_data.shape)
    minor_data_arr2, major_data_arr2 = seperate_minor_and_major_data(imbalanced_data)
    print(minor_data_arr2.shape)
    print(major_data_arr2.shape)
    # 测试Border_SMOTE方法
    balanced_data_arr2 = Border_SMOTE(imbalanced_data)
    print(balanced_data_arr2.shape)

（3）ADASYN算法

    ADASYN名为自适应合成抽样(adaptive synthetic sampling)，其最大的特点是采用某种机制自动决定每个少数类样本需要产生多少合成样本，而不是像SMOTE那样对每个少数类样本合成同数量的样本。

算法步骤如下：

1.首先计算需要合成的样本总量：

 

                                                    

 

    其中为多数类样本数量，为少数类样本数量，为系数。G即为总共想要合成的少数类样本数量，如果β=1则是合成后各类别数目相等。
​

2.对于每个少类别样本，找出其K近邻个点，并计算：

 

                                                  

 

    其中为K近邻个点中多数类样本的数量，Z为规范化因子以确保 构成一个分布。这样若一个少数类样本的周围多数类样本越多，则其 也就越高。

3.最后对每个少类别样本计算需要合成的样本数量，再用SMOTE算法合成新样本：

                                                 

 

优缺点：

    ADASYN利用分布来自动决定每个少数类样本所需要合成的样本数量，相当于给每个少数类样本赋了一个权重，周围的多数类样本越多则权重越高。

    ADASYN的缺点是易受离群点的影响，如果一个少数类样本的K近邻都是多数类样本，则其权重会变得相当大，进而会在其周围生成较多的样本。

 

三 参考资料

    以上内容有部分是借鉴了网上的资料，本人知识有限，若哪里写的不对，还望各位读者见谅并多多指教，下面贴出参考的一些资料清单：

[1]不平衡数据采样方法整理

[2]不平衡数据处理之SMOTE、Borderline SMOTE和ADASYN详解及Python使用

[3]机器学习之类别不平衡问题 (3) —— 采样方法