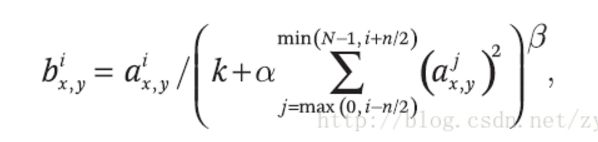经典卷积神经网络(2)--AlexNet卷积网络模型
背景
2012年,Hinton的学生Alex Krizhevsky借助深度学习相关理论提出了深度卷积网络模型AlexNet.在2012年ILSVRC竞赛中取得top-5错误率为15.3%,并取得大赛第一名。
和LeNet-5模型相比,AlexNet算是它的一个宽泛的版本。
AlexNet的结构如上图所示,共包含了8个学习层——5个卷积层与3个全连接层,相比于之前的LeNet-5网络,AlexNet有以下几个创新点:
1 使用ReLU激活函数
在过去,神经网络的激活函数通常是sigmoid或者tanh函数,这两种函数最大的缺点就是其饱和性,当输入的x过大或过小时,函数的输出会非常接近+1与-1,在这里斜率会非常小,那么在训练时引用梯度下降时,其饱和性会使梯度非常小,严重降低了网络的训练速度。 而ReLU的函数表达式为max(0, x),当x>0时输出为x,斜率恒为1,在实际使用时,神经网络的收敛速度要快过传统的激活函数数十倍。
2 利用多个GPU进行分布式计算
3 Local response normalization(局部响应归一化)
一般会在卷积层之后直接加上一个池化操作,但是AlexNet在卷积层和池化层之间加入了一个LRN层。Alex等人发现通过LRN这种归一化方式可以帮助提高网络的泛化性能。LRN的公式如下:
• bix,y,是归一化后的值,i是通道的位置,代表更新第几个通道的值,x与y代表待更新像素的位置。
• aix,y是输入值,是激活函数Relu的输出值,N是卷积核的个数。
• k、alpha、beta、n/2 都是自定义系数,可以先不用理会有什么用
LRN的作用就是,对位置(x, y)处的像素计算其与几个相邻的特征图的像素值的和,并除以这个和来归一化。特征图的顺序可以是任意的,在训练开始前确定顺序即可。其中的k, N, α, β都是超参数,论文中给出了所用的值为k=2, n=5, α=10e-4, β=0.75。在AlexNet中,LRN层位于ReLU之后。在论文中,Alex指出应用LRN后top-1与top-5错误率分别提升了1.4%与1.2%。
Hinton等人认为LRN层模仿生物神经系统的侧抑制机制,对局部神经元的活动创建竞争机制,使得响应比较大的值相对更大,并抑制其他响应较小的神经元,提高模型泛化能力。但是,后来的论文比如《Very Deep Convolution Networks for Large-Scale Image Recognition》(也就是提出VGG网络的文章)中证明,LRN对CNN并没有什么作用,反而增加了计算复杂度,因此,这一技术也不再使用了。
Tensorflow提供了nn.lrn()函数来实现LRN层的功能。
# 输入, n , K
tf.nn.lrn(input,depth_radius=None,bias=None,alpha=None,beta=None,name=None)4 Overlapping pooling
池化层是CNN中非常重要的一层,可以起到提取主要特征,减少特征图尺寸的作用,对加速CNN计算非常重要,然而通常池化的大小与步进被设置为相同的大小,当池化的大小大于步进时,就成为了overlapping pooling,这也是AlexNet中使用的池化技术。论文中提到,使用这种池化可以一定程度上减小过拟合现象。
5 Reducing Overfitting 减少过拟合
AlexNet中有六千万个参数,也非常容易产生过拟合现象,而AlexNet中采用了两种方式来对抗过拟合。
1.对抗过拟合最简单有效的办法就是扩大训练集的大小
训练时,对原始的256x256大小的图片随机裁剪为224x224大小,并进行随机翻转,这两种操作相当于增加了样本的数量。在测试时,AlexNet把输入图片与其水平翻转在四个角处与正中心共五个地方各裁剪下224x224大小的子图,即共裁剪出10个子图,均送入AlexNet中,并把10个softmax输出求平均,这个均值就是这张图片的最终预测结果。如果没有这些操作,AlexNet将出现严重的过拟合,使网络的深度不能达到这么深。
2.Dropout是神经网络中一种非常有效的减少过拟合的方法
在AlexNet中,在训练时,每层的keep_prob被设置为0.5。dropout只用于全连接层。
模型结构细节¶
- conv1阶段DFD(data flow diagram):
第一层输入数据为原始的227* 227* 3的图像(输入图像的尺寸是224* 224,在进行第一次卷积的时候会padding 3个像素变成227* 227),这个图像被11* 11* 3的卷积核进行卷积运算,卷积核对原始图像的每次卷积都生成一个新的像素。移动的步长是4个像素。因此,卷积核在移动的过程中会生成(227-11)/4+1=55个像素,共有96个卷积核,会生成555596个卷积后的像素层。96个卷积核分成2组,每组48个卷积核。对应生成2组55* 55* 48的卷积后的像素层数据。这些像素层经过relu1单元的处理,生成激活像素层,尺寸仍为2组55* 55* 48的像素层数据。
这些像素层经过pool(池化)的处理,池化核的尺度为3* 3,步长为2,则池化后图像的尺寸为(55-3)/2+1=27。 即池化后像素的规模为27* 27* 96;然后经过LRN归一化处理;第一卷积层运算结束后形成的像素层的规模为27* 27* 96。这96层像素层分为2组,每组48个像素层,每组在一个独立的GPU上进行运算。
conv2阶段DFD(data flow diagram):
第二层输入数据为第一层输出的27* 27* 96的像素层,272796的像素数据分成272748的两组像素数据,两组数据分别再两个不同的GPU中进行运算。每个卷积核尺寸为55*48,步长是1个像素。因此,卷积核在移动的过程中会生成(27-5+2 2)/1+1=27个像素。共有256个尺寸为5* 548的卷积核;这256个卷积核分成两组,每组针对一个GPU中的272748的像素进行卷积运算。会生成两组27 27* 128个卷积后的像素层。这些像素层经过relu2单元的处理,生成激活像素层,尺寸仍为两组2727128的像素层。
这些像素层经过pool运算(池化运算)的处理,池化核的尺度为3* 3,运算的步长为2,则池化后图像的尺寸为(27-3)/2+1=13。 即池化后像素的规模为2组131 3 128的像素层;然后经过LRN归一化处理;第二卷积层运算结束后形成的像素层的规模为2组13* 13* 128的像素层。分别对应2组128个卷积核所运算形成。每组在一个GPU上进行运算。即共256个卷积核,共2个GPU进行运算。
conv3阶段DFD(data flow diagram):
第三层输入数据为第二层输出的2组13* 13* 128的像素层;每个GPU中都有192个卷积核,每个卷积核的尺寸是3* 3* 256。每个GPU中的卷积核都能对2组13* 13* 128的像素层的所有数据进行卷积运算。步长是1个像素。因此,运算后的卷积核的尺寸为(13-3+1* 2)/1+1=13。这些像素层经过relu3单元的处理,生成激活像素层,尺寸仍为2组13* 13* 192像素层。
conv4阶段DFD(data flow diagram):
conv5阶段DFD(data flow diagram):
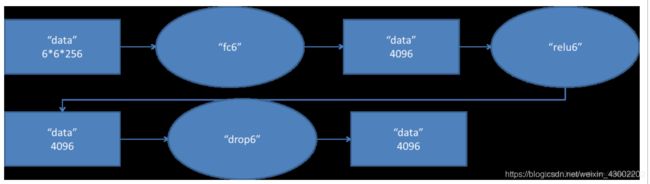
fc6阶段DFD(data flow diagram):
卷积核大小66*2564096,共有4096个卷积核;每个6* 6*256尺寸的滤波器对第六层的输入数据进行卷积运算生成一个运算结果。
卷积核和输入数据大小一样,因此可将该层看作全连层。
fc7阶段DFD(data flow diagram):
第七层有4096个神经元节点
第六层输出的4096个数据与第七层的4096个神经元进行全连接,然后经由relu7进行处理后生成4096个数据,再经过dropout7处理后输出4096个数据。
fc8阶段DFD(data flow diagram):
第八层有1000个神经元节点
#第七层输出的4096个数据与第八层的1000个神经元进行全连接,经过训练后输出被训练的数值。
import tensorflow as tf
import math
import time
from datetime import datetime #导入datetime库中的datetime类
batch_size = 32
num_batches = 100
# 在函数inference_op()内定义前向传播的过程
def inference_op(images):
parameters = [] #在反向传播时要调用
# 在命名空间conv1下实现第一个卷积层
with tf.name_scope("conv1"):
kernel = tf.Variable(tf.truncated_normal([11, 11, 3, 96], dtype=tf.float32,
stddev=1e-1), name="weights")
conv = tf.nn.conv2d(images, kernel, [1, 4, 4, 1], padding="SAME")
biases = tf.Variable(tf.constant(0.0, shape=[96], dtype=tf.float32),
trainable=True, name="biases")
conv1 = tf.nn.relu(tf.nn.bias_add(conv, biases))
# 打印第一个卷积层的网络结构
print(conv1.op.name, ' ', conv1.get_shape().as_list())
parameters += [kernel, biases]
# 添加一个LRN层和最大池化层
lrn1 = tf.nn.lrn(conv1, 4, bias=1.0, alpha=0.001 / 9.0, beta=0.75, name="lrn1")
pool1 = tf.nn.max_pool(lrn1, ksize=[1, 3, 3, 1], strides=[1, 2, 2, 1],
padding="VALID", name="pool1")
# 打印池化层网络结构
print(pool1.op.name, ' ', pool1.get_shape().as_list())
# 在命名空间conv2下实现第二个卷积层
with tf.name_scope("conv2"):
kernel = tf.Variable(tf.truncated_normal([5, 5, 96, 256], dtype=tf.float32,
stddev=1e-1), name="weights")
conv = tf.nn.conv2d(pool1, kernel, [1, 1, 1, 1], padding="SAME")
biases = tf.Variable(tf.constant(0.0, shape=[256], dtype=tf.float32),
trainable=True, name="biases")
conv2 = tf.nn.relu(tf.nn.bias_add(conv, biases))
parameters += [kernel, biases]
# 打印第二个卷积层的网络结构
print(conv2.op.name, ' ', conv2.get_shape().as_list())
# 添加一个LRN层和最大池化层
lrn2 = tf.nn.lrn(conv2, 4, bias=1.0, alpha=0.001 / 9.0, beta=0.75, name="lrn2")
pool2 = tf.nn.max_pool(lrn2, ksize=[1, 3, 3, 1], strides=[1, 2, 2, 1],
padding="VALID", name="pool2")
# 打印池化层的网络结构
print(pool2.op.name, ' ', pool2.get_shape().as_list())
# 在命名空间conv3下实现第三个卷积层
with tf.name_scope("conv3"):
kernel = tf.Variable(tf.truncated_normal([3, 3, 256, 384],
dtype=tf.float32, stddev=1e-1),
name="weights")
conv = tf.nn.conv2d(pool2, kernel, [1, 1, 1, 1], padding="SAME")
biases = tf.Variable(tf.constant(0.0, shape=[384], dtype=tf.float32),
trainable=True, name="biases")
conv3 = tf.nn.relu(tf.nn.bias_add(conv, biases))
parameters += [kernel, biases]
# 打印第三个卷积层的网络结构
print(conv3.op.name, ' ', conv3.get_shape().as_list())
# 在命名空间conv4下实现第四个卷积层
with tf.name_scope("conv4"):
kernel = tf.Variable(tf.truncated_normal([3, 3, 384, 384],
dtype=tf.float32, stddev=1e-1),
name="weights")
conv = tf.nn.conv2d(conv3, kernel, [1, 1, 1, 1], padding="SAME")
biases = tf.Variable(tf.constant(0.0, shape=[384], dtype=tf.float32),
trainable=True, name="biases")
conv4 = tf.nn.relu(tf.nn.bias_add(conv, biases))
parameters += [kernel, biases]
# 打印第四个卷积层的网络结构
print(conv4.op.name, ' ', conv4.get_shape().as_list())
# 在命名空间conv5下实现第五个卷积层
with tf.name_scope("conv5"):
kernel = tf.Variable(tf.truncated_normal([3, 3, 384, 256],
dtype=tf.float32, stddev=1e-1),
name="weights")
conv = tf.nn.conv2d(conv4, kernel, [1, 1, 1, 1], padding="SAME")
biases = tf.Variable(tf.constant(0.0, shape=[256], dtype=tf.float32),
trainable=True, name="biases")
conv5 = tf.nn.relu(tf.nn.bias_add(conv, biases))
parameters += [kernel, biases]
# 打印第五个卷积层的网络结构
print(conv5.op.name, ' ', conv5.get_shape().as_list())
# 添加一个最大池化层
pool5 = tf.nn.max_pool(conv5, ksize=[1, 3, 3, 1], strides=[1, 2, 2, 1],
padding="VALID", name="pool5")
# 打印最大池化层的网络结构
print(pool5.op.name, ' ', pool5.get_shape().as_list())
# 将pool5输出的矩阵汇总为向量的形式,为的是方便作为全连层的输入
pool_shape = pool5.get_shape().as_list()
nodes = pool_shape[1] * pool_shape[2] * pool_shape[3]
reshaped = tf.reshape(pool5, [pool_shape[0], nodes])
# 创建第一个全连接层
with tf.name_scope("fc_1"):
fc1_weights = tf.Variable(tf.truncated_normal([nodes, 4096], dtype=tf.float32,
stddev=1e-1), name="weights")
fc1_bias = tf.Variable(tf.constant(0.0, shape=[4096],
dtype=tf.float32), trainable=True, name="biases")
fc_1 = tf.nn.relu(tf.matmul(reshaped, fc1_weights) + fc1_bias)
parameters += [fc1_weights, fc1_bias]
# 打印第一个全连接层的网络结构信息
print(fc_1.op.name, ' ', fc_1.get_shape().as_list())
# 创建第二个全连接层
with tf.name_scope("fc_2"):
fc2_weights = tf.Variable(tf.truncated_normal([4096, 4096], dtype=tf.float32,
stddev=1e-1), name="weights")
fc2_bias = tf.Variable(tf.constant(0.0, shape=[4096],
dtype=tf.float32), trainable=True, name="biases")
fc_2 = tf.nn.relu(tf.matmul(fc_1, fc2_weights) + fc2_bias)
parameters += [fc2_weights, fc2_bias]
# 打印第二个全连接层的网络结构信息
print(fc_2.op.name, ' ', fc_2.get_shape().as_list())
# 返回全连接层处理的结果
return fc_2, parameters
#通过Graph类的as_default()函数定义一个默认计算图
with tf.Graph().as_default():
# 创建模拟的图片数据.
image_size = 224
images = tf.Variable(tf.random_normal([batch_size, image_size, image_size, 3],
dtype=tf.float32, stddev=1e-1))
# 在计算图中定义前向传播模型的运行,并得到不包括全连部分的参数
# 这些参数用于之后的梯度计算
fc_2, parameters = inference_op(images)
init_op = tf.global_variables_initializer()
#tf.ConfigProto()主要的作用是配置tf.Session的运算方式,比如gpu运算或者cpu运算
# gpu_options.allocator_type 用于设置GPU的分配策略,值为"BFC"表示采用最佳适配合并算法
config = tf.ConfigProto()
config.gpu_options.allocator_type = "BFC"
with tf.Session(config=config) as sess:
sess.run(init_op)
num_steps_burn_in = 10
total_dura = 0.0 #总耗时的初始值
total_dura_squared = 0.0 #耗时平方和的初始值
back_total_dura = 0.0 #反向传播的总耗时,耗时平方和的初始值
back_total_dura_squared = 0.0
for i in range(num_batches + num_steps_burn_in): #P298
start_time = time.time()
_ = sess.run(fc_2)
duration = time.time() - start_time #每一轮前向传播的的耗时
if i >= num_steps_burn_in:
if i % 10 == 0:
print('%s: step %d, duration = %.3f' %
(datetime.now(), i - num_steps_burn_in, duration)) #当前日期时间,起始轮数,该轮耗时
total_dura += duration
total_dura_squared += duration * duration
average_time = total_dura / num_batches
# 打印前向传播的运算时间信息
print('%s: Forward across %d steps, %.3f +/- %.3f sec / batch' %
(datetime.now(), num_batches, average_time,
math.sqrt(total_dura_squared / num_batches - average_time * average_time)))
# 使用gradients()求相对于fc_2的L2 loss的所有模型参数的梯度 #L2 loss:对output求L2范数作为损失函数
# 函数原型gradients(ys,xs,grad_ys,name,colocate_gradients_with_ops,gate_gradients,
# aggregation_method=None)
# 一般情况下我们只需对参数ys、xs传递参数,他会计算ys相对于xs的偏导数,并将
# 结果作为一个长度为len(xs)的列表返回,其他参数在函数定义时都带有默认值,
# 比如grad_ys默认为None,name默认为gradients,colocate_gradients_with_ops默认
# 为False,gate_gradients默认为False
grad = tf.gradients(tf.nn.l2_loss(fc_2), parameters)
# 运行反向传播测试过程
for i in range(num_batches + num_steps_burn_in):
start_time = time.time()
_ = sess.run(grad)
duration = time.time() - start_time
if i >= num_steps_burn_in:
if i % 10 == 0:
print('%s: step %d, duration = %.3f' %
(datetime.now(), i - num_steps_burn_in, duration))
back_total_dura += duration
back_total_dura_squared += duration * duration
back_avg_t = back_total_dura / num_batches
# 打印反向传播的运算时间信息
print('%s: Forward-backward across %d steps, %.3f +/- %.3f sec / batch' %
(datetime.now(), num_batches, back_avg_t,
math.sqrt(back_total_dura_squared / num_batches - back_avg_t * back_avg_t)))