【每日挠头算法题】LeetCode 1337. 矩阵中战斗力最弱的 K 行 —— 二分 + 排序 / 堆

作者主页：@进击的安度因
学习社区：进击的安度因（个人社区）
专栏链接：每日挠头算法题

一、题目描述

今天的题目其实可以暴力求解，但是我们今天主要为了讲解 二分 和 堆，以练习为主~

链接：1337. 矩阵中战斗力最弱的 K 行

描述：

给你一个大小为 m * n 的矩阵 mat，矩阵由若干军人和平民组成，分别用 1 和 0 表示。

请你返回矩阵中战斗力最弱的 k 行的索引，按从最弱到最强排序。

如果第 i 行的军人数量少于第 j 行，或者两行军人数量相同但 i 小于 j，那么我们认为第 i 行的战斗力比第 j 行弱。

军人 总是 排在一行中的靠前位置，也就是说 1 总是出现在 0 之前。

示例1：

输入：mat = 
[[1,1,0,0,0],
 [1,1,1,1,0],
 [1,0,0,0,0],
 [1,1,0,0,0],
 [1,1,1,1,1]], 
k = 3
输出：[2,0,3]
解释：
每行中的军人数目：
行 0 -> 2 
行 1 -> 4 
行 2 -> 1 
行 3 -> 2 
行 4 -> 5 
从最弱到最强对这些行排序后得到 [2,0,3,1,4]

示例2：

输入：mat = 
[[1,0,0,0],
 [1,1,1,1],
 [1,0,0,0],
 [1,0,0,0]], 
k = 2
输出：[0,2]
解释： 
每行中的军人数目：
行 0 -> 1 
行 1 -> 4 
行 2 -> 1 
行 3 -> 1 
从最弱到最强对这些行排序后得到 [0,2,3,1]

提示：

• m == mat.length
• n == mat[i].length
• 2 <= n, m <= 100
• 1 <= k <= m
• matrix[i][j] 不是 0 就是 1

二、思路及代码实现

首先梳理一下题目大意：

给定一个矩阵，矩阵元素由 1 和 0 组成，1 为军人，0 为平民。军人数量就是矩阵的战斗力。军人 1 出现在矩阵每一行的 靠前位置 。

如果 第 i 行 1 数量少于第 j 行，或者第 i 行和第 j 行 1 的数量相同，但是 i < j 那么认为 第 i 行的战斗力 比第 j 行弱 。

题目要求返回前 k 行的索引，就是按照顺序返回 1 最少的前 k 行。

所以这道题目先得求出每行的 1 的个数：

求每行 1 的个数可以通过遍历每一行来实现，但是我认为最好的方法还是 二分 。

由于二维数组每行是从 1 开始，到 0 结束，所以数组整体是有序的。那么我只需要二分出 1 的 右边界点 就可以了。

但是要求出前 k 行战斗力最弱的索引仅有 战斗力 是没用的，我们需要之后比较战斗力的同时返回相应索引，并且对于战斗力相同的情况下需要比较 索引的大小 。所以需要考虑一下 用什么存储数据 。

了解了这些，我们接下来讲解我们的主要解法。解法分为两种：二分 + 排序 和 二分 + 小堆 。

1. 二分 + 排序

这里我们采用的二分方式是 二分出右边界点 ，用之前的二分模板：

// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

每次二分需要将 每行中1的个数 和 当前行数 存储到对应的空间中。

所以我们可以定义一个结构体，用来专门存放两种类型的数据：

typedef struct data
{
    int combat; // 战斗力
    int row; // 行数
}data;

紧接着动态开辟一个结构体数组 tmp ，用来存储数据；一个 k 个大小的数组 res 作为返回的数组。

在二分的过程中：

• 如果二分出来的边界点的值 不等于 1 ，说明二分结果错误，那么此行战斗力 combat 为 0 ，存到正确位置
• 如果二分出来的边界点的值 等于 1 ，说明二分结果正确，将 l(r) + 1 存入结构体数组的对应位置

有了结构体数组，那么进行排序就好了，这里直接使用 qsort ，注意需要处理一下 特殊情况 ：第 i 行和第 j 行 1 的数量相同，但是 i < j 那么认为 第 i 行的战斗力 比第 j 行弱 。

最后将数据存入返回数组中，返回即可。

过程相对简单，直接上代码：

typedef struct data
{
    int combat; // 战斗力
    int row; // 行
}data;

int cmp(const void* e1, const void* e2)
{
    data* ee1 = (data*)e1;
    data* ee2 = (data*)e2;
    // 战斗力大小 或 战斗力相等 行数不同
    return (ee1->combat > ee2->combat) || (ee1->combat == ee2->combat && ee1->row > ee2->row);
}

int* kWeakestRows(int** mat, int matSize, int* matColSize, int k, int* returnSize)
{
    // 答案数组
    int* res = (int*)malloc(sizeof(int) * k);
    data* tmp = (data*)malloc(sizeof(data) * matSize);
    int col = *matColSize;
    *returnSize = k;

    // 二分，将数据存入 tmp 中
    for (int i = 0; i < matSize; i++) {
        int l = 0, r = col - 1;
        while (l < r) {
            int mid = l + r + 1 >> 1;
            if (mat[i][mid] == 1) {
                l = mid;
            } else if (mat[i][mid] == 0) {
                r = mid - 1;
            }
        }
        if (mat[i][l] != 1) {
            tmp[i].combat = 0; // 无战斗力
        } else {
            tmp[i].combat = l + 1;
        }
        tmp[i].row = i; // 存入索引
    }
    
    qsort(tmp, matSize, sizeof(data), cmp);

    for (int i = 0; i < k; i++)
    {
        res[i] = tmp[i].row;
    }

    return res;
}

2. 二分 + 堆

这种方法其实是我第一次就想到的，但是中途调试了很久，觉得这种思路比排序难一些就把它放到第二个。

先讲常规操作：

这里我们采用的存储结构是用 二维数组 ，将其定义为全局变量 int heap[100][2] ：

将每一行看作是一个元素，存放 战斗力 和 索引 。

开辟一个 ans 作为返回数组。

紧接着就是二分，并将元素 战斗力存入二维数组每行的 0 下标处，将 行的索引存入二维数组每行的 1 下标处 。

准备工作完成，接下来开始讲解剩余步骤。

我想到堆的原因就是因为之前的堆排序和TopK当时我看了很久，看这道题题目我就觉得可以用堆解决。

之前说过建堆的优先级是 向下调整建堆 > 向上调整建堆 ，我们当前使用 向下调整算法 来构建一个大小为矩阵的行数的 小堆 。

直接使用 heap 这个全局数组，以它为基准来建堆。

就拿我们 示例1 给出的矩阵计算出的结果作为堆中的数据，计算结果为：

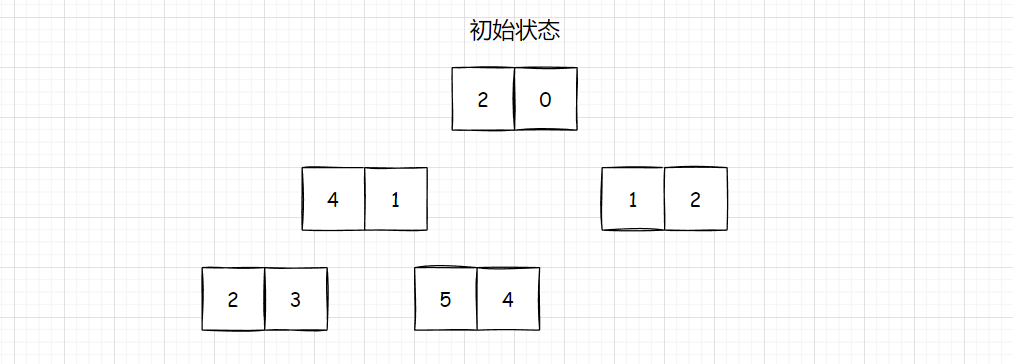
• heap[0][0] = 2 heap[0][1] = 0
• heap[1][0] = 4 heap[1][1] = 1
• heap[2][0] = 1 heap[2][1] = 2
• heap[3][0] = 2 heap[3][1] = 3
• heap[4][0] = 5 heap[4][1] = 4

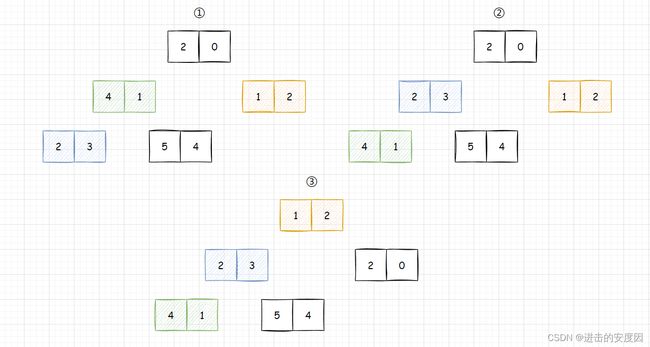
将其写成堆的样子：

接着就是写 向下调整算法 ，向下调整算法需要注意几点：

• 小堆是由 战斗力强弱 起主要衡量，战斗力相等需要看行之间的关系
• 构建的是小堆，每次交换的是最小孩子
• 求最小孩子时，需要额外判断战斗力相等时的情况
• 判断调整时也需要判断战斗力相等的情况
• 交换数据时，由于这里是二维数组，所以是交换一行的数据，传参传每行的地址，交换函数的参数要写成二级指针

构建过程：

最后我们需要 索引 放入返回数组中：

主要方法是给定一个 end 等于 当前堆的行数 。

在循环 k 次，先将 二维数组第一行第二列的元素 存入返回数组 ans 中，然后交换堆顶和堆底的元素。

向下调整重新建堆，将 end-- ，每次丢弃堆中1个元素，最后 ans 中的结果就是战斗力最弱的 K 行 。

接下来看看代码怎么写：

int heap[100][2];

void Swap(int** p1, int** p2)
{
    int* tmp = *p1;
    *p1 = *p2;
    *p2 = tmp;
}

// 向下调整
void AdjustDown(int n, int parent)
{
    int child = 2 * parent + 1;

    while (child < n) {
        // 求最小孩子
        if (child + 1 < n && (heap[child + 1][0] < heap[child][0] || (heap[child + 1][0] == heap[child][0] && heap[child + 1][1] < heap[child][1]))) {
            child++;
        }
        // 判断是否调整
        if (heap[child][0] < heap[parent][0] || (heap[child][0] == heap[parent][0] && heap[child][1] < heap[parent][1])) {
            // 交换两行
            Swap(heap[child], heap[parent]);
            parent = child;
            child = 2 * parent + 1;
        } else {
            break;
        }
    }
}

int* kWeakestRows(int** mat, int matSize, int* matColSize, int k, int* returnSize)
{
    int cnt = 0;
    *returnSize = k;
    for (int i = 0; i < matSize; i++) {
        // 将 k 行元素的索引存入 heap 中
        int l = 0, r = *matColSize - 1;
        while (l < r) {
            int mid = l + r + 1>> 1;
            if (mat[i][mid] == 0) {
                r = mid - 1;
            }
            if (mat[i][mid] == 1) {
                l = mid;
            }
        }
        // 0 下标处存战斗力
        // 1 下标处存索引
        if (mat[i][l] != 1)
        {
            heap[cnt][0] = 0;
        } else {
            heap[cnt][0] = l + 1;
        }
        heap[cnt][1] = i;
        cnt++;
    }

    // 将 res 数组中元素建小堆，不断取出堆顶元素
    int* ans = (int*)malloc(sizeof(int) * k);
    for (int i = (cnt - 1 - 1) / 2; i >= 0; i--) {
        // 向下调整堆中元素
        AdjustDown(cnt, i);
    }

    int end = cnt - 1, j = 0;
    while (k > 0) {
        // 将索引存入 ans 数组
        ans[j++] = heap[0][1];
        Swap(heap[0], heap[end]);
        AdjustDown(end--, 0);
        k--;
    }
    return ans;
}

完结撒花