神经网络之梯度下降法原理
0. 前言
梯度下降法是神经网络的一个优化算法,在回调权值的过程中有重要的作用,下面先回顾一下神经网络指明一下梯度下降在何时用上。
1. 回顾神经网络
先来回归一下神经网络的学习过程,如下图:

上图是一个模型,其中w是参数,也是我们说的权重,x是输入的数据。w和x运算之后得到的h是输出结果。假设期望结果(实际值)是y,损失是loss,则:
h h h = w x wx wx
l o s s = ( h − y ) 2 = ( w x − y ) 2 loss = (h-y)^2 = (wx-y)^2 loss=(h−y)2=(wx−y)2
求解目标就是使得损失loss最小
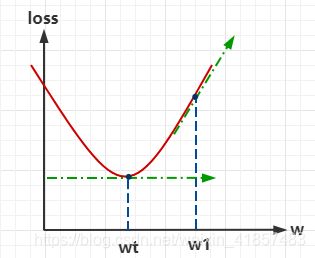
从上图中可以看到,损失在 w t w_t wt时最小,即在 w t w_t wt时导数为0。在数学上,我们可以通过公式定理直接求得某个函数的导数,再直接求得最小值,但在计算机中却需要经过一定的过程。
2. 基本原理
用下图来讲解一下导数的几何意义

若对 x 0 x_0 x0这点求导,即 f ( x 0 ) ′ f(x_0)' f(x0)′,此处导数的几何意义就是这一点在函数图像上的切线,也叫斜率、梯度。
下面,回到前面loss-w的图像:
模型开始,会随机取一个 w w w的值,此处假定为 w 1 w_1 w1:

这时的 w 1 w_1 w1对应的损失比较大,所以先对其进行求导,现在希望得到下一时刻的 w t w_t wt值,如果损失要变小,就要在 w 1 w_1 w1左侧。此时,梯度下降的思想就出来的,先看下面的式子:
W t = W 1 + ( − α ∗ d w ) W_t = W_1 + (-\alpha*dw) Wt=W1+(−α∗dw)
在 w 1 w_1 w1处,求导( d w dw dw)后,要继续减小损失, α \alpha α是移动的一个步长,移动之后,此处是往左侧移动,所以就是 W 1 + ( − α ∗ d w ) W_1 + (-\alpha*dw) W1+(−α∗dw)得到下一个 w t w_t wt的值。经过多次上述过程重复的运算,就可以得到一个最佳的 w w w的值。
到这一步,也许你还是没有特别清楚。别着急,下面举一个实际的例子来进行说明,进很好理解了!
3. 举例说明
用 y = x 2 y = x^2 y=x2 这个式子来进行说明,即求解这个函数的最小值。
通过数学的方法可以知道,它是在 x = 0 x=0 x=0的时候取得最小值0.
现在,先把它的函数图像画出来:
前面说了,在计算机中,是通过不断尝试求得最小值,下面模拟一下这个过程。
补充
在数学上有如下定理:
- 若对任意 x ∈ ( a , b ) x∈(a, b) x∈(a,b),都有 f ′ ( x ) > 0 f'(x)>0 f′(x)>0,则 f ( x ) f(x) f(x)在 [ a , b ] [a,b] [a,b]上单增;
- 若对任意 x ∈ ( a , b ) x∈(a, b) x∈(a,b),都有 f ′ ( x ) < 0 f'(x)<0 f′(x)<0 ,则 f ( x ) f(x) f(x)在 [ a , b ] [a,b] [a,b]上单减;
① 首先,假设初始 x 0 = 2 x_0 = 2 x0=2,这一点的导数是 y ′ ( x 0 ) = 2 x 0 = 4 > 0 y'(x_0) = 2x_0 = 4 > 0 y′(x0)=2x0=4>0 ,导数大于0,是递增的,即 x ↑ x\uparrow x↑, y ↑ y\uparrow y↑;因为我们的目标是求解 y y y 的最小值,所以下一步要减小 x x x 的值;
② x 1 < x 0 x_1
② x 2 > x 1 x_2>x_1 x2>x1 是显而易见的,假设此时 x 2 = 1.2 x_2 = 1.2 x2=1.2,这一点的导数是 y ′ ( x 2 ) = 2 x 2 = 2.4 > 0 y'(x_2) = 2x_2 = 2.4 > 0 y′(x2)=2x2=2.4>0 ,导数大于0,是递增的,即 x ↑ x\uparrow x↑, y ↑ y\uparrow y↑;因为我们的目标是求解 y y y 的最小值,所以下一步要减小 x x x 的值;
③ x 3 < x 2 x_3
需要不断重复上面的这个过程来不断逼近最小值,即迭代。
再次简化一下这个过程:
① x 0 = 2 x_0 = 2 x0=2, y ′ ( x 0 ) = 4 > 0 y'(x_0) = 4 > 0 y′(x0)=4>0, x ↑ x\uparrow x↑ y ↑ y\uparrow y↑;
② x 1 = x 0 − Δ 0 x_1 = x_0 -\Delta_0 x1=x0−Δ0
x 1 = − 1.3 x_1 = -1.3 x1=−1.3, y ′ ( x 1 ) = − 2.6 < 0 y'(x_1) = -2.6 < 0 y′(x1)=−2.6<0, x ↑ x\uparrow x↑ y ↓ y\downarrow y↓;
③ x 2 = x 1 + Δ 1 x_2 = x_1 +\Delta_1 x2=x1+Δ1
x 2 = 1.2 x_2 = 1.2 x2=1.2, y ′ ( x 2 ) = 2.4 > 0 y'(x_2) = 2.4 > 0 y′(x2)=2.4>0, x ↑ x\uparrow x↑ y ↑ y\uparrow y↑;
④ …
现在,对于整个过程理清楚了,但是还是有很多问题:
- 在上面的过程中,递增就减小 x x x 的取值,递减就增大 x x x 的取值,对于增大和减小的那些 Δ \Delta Δ 有没有通用的取值?
- 对于上面的 + + +和 − - −能否统一符号?
即能否用一个通式来表示上面这个过程?
通过观察上面的式子,可以看到,是 + + + 还是 − - −,取决于求导之后是大于0还是小于0;所以可以直接让 Δ > 0 \Delta>0 Δ>0,只要前面是负号,再根据其求导的正负就能确定最终是 + + + 还是 − - −
也就是可以写成下面的式子:
x k + 1 = x k − Δ f ′ ( x k ) x_{k+1} = x_k - \Delta f'(x_k) xk+1=xk−Δf′(xk)
Δ \Delta Δ有时候也用 α \alpha α表示,这是步长,也称作学习率,一般大于0;也就是说 Δ \Delta Δ 控制我们每次调整的大小, f ′ ( x k ) f'(x_k) f′(xk) 控制方向。
在求导为正的时候,就是 x k x_k xk 减去某个值,求导为负的时候,就是 x k x_k xk 加上某个值。
这就是对神经网络中梯度下降这个优化算法的整个说明了,下一篇博客打算用代码来模拟一下这个过程。
