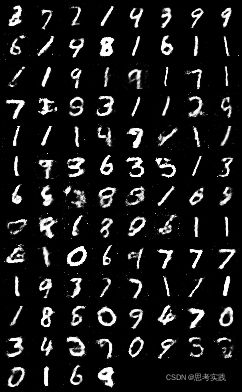Pytorch_GAN_mnist细节讲解从理论到实践
目录
理论部分
代码部分
理论部分
理论部分,网上一大堆资料,按自己的思路整理了一遍,尽量把每个细节(理论、公式、训练方式、代码),给大家讲解清楚,个人花了一天时间入门Gan的基础,其实对于大部分人都是做应用,但是还是如果感兴趣,还是得花功夫在数学上,里面一些细节的推导,设计到数学基础,就会感觉有些许吃力,不过说实话,目前的遇见的问题数学基础还都只是大学数学就能解释的。
//从简洁的概念解释,到GAN的loss函数的理解,训练方式,GAN的理论强大之处
简单理解与实验生成对抗网络GAN_我爱智能-CSDN博客_生成对抗网络
GAN目标函数的理解
GAN目标函数的理解_网络安全小菜狗的博客-CSDN博客
简单理解与实验生成对抗网络GAN_我爱智能-CSDN博客_生成对抗网络
//关于数学推导部分,这是最详细的部分了,如果觉得基础不太好,可以去看paddle_gan的视频讲解
GAN入门理解及公式推导 - 知乎
生成对抗网络(GAN)的数学原理全解//有收获,但挺标题党的不如前一个数学严密
生成对抗网络(GAN)的数学原理全解 - 知乎
伪代码算法训练过程
看了上面的一些资料,我相信你对GAN的原理已经有了大概的认识了,很大程度上要理解一个深度学习模型算法,除了他的结构上的原理,还有很重要的一点,就是衡量输出结果与预测结果的好坏,也就是loss函数,深度学习各种框架让我们感觉loss函数好像很简单,其实当你深入为什么选择某种loss函数,loss函数与你的模型息息相关,你会对loss函数图像的下降有进一步的理解。
一文搞懂交叉熵在机器学习中的使用,透彻理解交叉熵背后的直觉_史丹利复合田的博客-CSDN博客_交叉熵的理解
笔记 | 什么是Cross Entropy//讲的直白,数学的严肃理论推导也在参考资料中,总体来说,不错。
笔记 | 什么是Cross Entropy - 知乎
P为真实样本的分布,Q为生成数据的分布,大概是说KL散度越小,这是一种衡量模型训练的标准,表示q分布和p分布越接近,可以说生成器就训练的比较好了,loss越小,说明P分布与Q分布约接近,G网络生成的图片也就越逼真,这样也到达了目的。
代码部分
通常来说都是先训练的D再训练的G,可以看伪代码和第一个上方的第一个链接。
完整代码:Pytorch_example: 使用Pytorch完成的任务 - Gitee.com
代码参考的资料部分
案例带你学Pytorch系列(3)——GAN生成对抗网络
PyTorch搭建GAN网络
import os
import torch
import torchvision
import torch.nn as nn
from torchvision import transforms
from torchvision.utils import save_image
# Device configuration
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
# Hyper-parameters
latent_size = 64
hidden_size = 256
image_size = 784
num_epochs = 200
batch_size = 100
sample_dir = 'samples'
# Create a directory if not exists
if not os.path.exists(sample_dir):
os.makedirs(sample_dir)
# Image processing
# transform = transforms.Compose([
# transforms.ToTensor(),
# transforms.Normalize(mean=(0.5, 0.5, 0.5), # 3 for RGB channels
# std=(0.5, 0.5, 0.5))])
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize(mean=[0.5], # 1 for greyscale channels
std=[0.5])])
# MNIST dataset
mnist = torchvision.datasets.MNIST(root='../../data/',
train=True,
transform=transform,
download=True)
# Data loader
data_loader = torch.utils.data.DataLoader(dataset=mnist,
batch_size=batch_size,
shuffle=True)
# Discriminator
D = nn.Sequential(
nn.Linear(image_size, hidden_size),#28*28(image)through dataloader->784->256
nn.LeakyReLU(0.2),
nn.Linear(hidden_size, hidden_size),#256->256
nn.LeakyReLU(0.2),
nn.Linear(hidden_size, 1),#256->1
nn.Sigmoid())#scale 0-1
# Generator
G = nn.Sequential(
nn.Linear(latent_size, hidden_size),#64->256
nn.ReLU(),
nn.Linear(hidden_size, hidden_size),#256->256
nn.ReLU(),
nn.Linear(hidden_size, image_size),#256->784
nn.Tanh())
# Device setting
D = D.to(device)
G = G.to(device)
# Binary cross entropy loss and optimizer:告诉生成数据的分布与真实数据的分布有多大的距离
criterion = nn.BCELoss()
d_optimizer = torch.optim.Adam(D.parameters(), lr=0.0002)
g_optimizer = torch.optim.Adam(G.parameters(), lr=0.0002)
def denorm(x):
out = (x + 1) / 2
return out.clamp(0, 1)
# ================================================================== #
# 像素值出现在(-1,1)的原因是:
# transforms.ToTensor()将图片归一化到(0,1)
# transforms.Normalize([0.5, 0.5, 0.5], [0.5, 0.5, 0.5])])将图片归一化到(-1,1)#
# ================================================================== #
def reset_grad():
d_optimizer.zero_grad()
g_optimizer.zero_grad()
# Start training
total_step = len(data_loader)
for epoch in range(num_epochs):
for i, (images, _) in enumerate(data_loader):
images = images.reshape(batch_size, -1).to(device)#shape(100,784)
# Create the labels which are later used as input for the BCE loss
real_labels = torch.ones(batch_size, 1).to(device)
fake_labels = torch.zeros(batch_size, 1).to(device)
# ================================================================== #
# Train the discriminator #
# ================================================================== #
# Compute BCE_Loss using real images where (x, y): - y * log(D(x)) - (1-y) * log(1 - D(x))
# Second term of the loss is always zero since real_labels == 1
outputs = D(images)
d_loss_real = criterion(outputs, real_labels)
real_score = outputs
# Compute BCELoss using fake images
# First term of the loss is always zero since fake_labels == 0
z = torch.randn(batch_size, latent_size).to(device)#高斯随机分布数据按生成模型输入的size给出
fake_images = G(z)
outputs = D(fake_images)
d_loss_fake = criterion(outputs, fake_labels)
fake_score = outputs
# Backprop and optimize
d_loss = d_loss_real + d_loss_fake
#GAN目标函数的理解:https://blog.csdn.net/weixin_42101364/article/details/115750844
reset_grad()
d_loss.backward()
d_optimizer.step()
# ================================================================== #
# Train the generator #
# ================================================================== #
# Compute loss with fake images
z = torch.randn(batch_size, latent_size).to(device)
fake_images = G(z)
outputs = D(fake_images)#outputs is equal to D(G(Z))
#(x, y): - y * log(D(x)) - (1-y) * log(1 - D(x))
# We train G to maximize log(D(G(z)) instead of minimizing log(1-D(G(z)))
# For the reason, see the last paragraph of section 3. https://arxiv.org/pdf/1406.2661.pdf
g_loss = criterion(outputs, real_labels)#我们说这个时候是希望假样本的标签是1的,基于这一点,可以理解,这样就可以去很好的定义loss
# Backprop and optimize
reset_grad()
g_loss.backward()
g_optimizer.step()
if (i+1) % 200 == 0:
print('Epoch [{}/{}], Step [{}/{}], d_loss: {:.4f}, g_loss: {:.4f}, D(x): {:.2f}, D(G(z)): {:.2f}'
.format(epoch, num_epochs, i+1, total_step, d_loss.item(), g_loss.item(),
real_score.mean().item(), fake_score.mean().item()))
# Save real images
if (epoch+1) == 1:
images = images.reshape(images.size(0), 1, 28, 28)#(batch_size,channel,width,height)
save_image(denorm(images), os.path.join(sample_dir, 'real_images.png'))
# Save sampled images
fake_images = fake_images.reshape(fake_images.size(0), 1, 28, 28)
save_image(denorm(fake_images), os.path.join(sample_dir, 'fake_images-{}.png'.format(epoch+1)))
# Save the model checkpoints
torch.save(G.state_dict(), 'G.ckpt')
torch.save(D.state_dict(), 'D.ckpt')这里因为我们的epoch是200,save fake images在每个epoch里面,也就保存了200多张fake images,每张图片都是batchsize=100也就是100个数字,在 if(epoch+1)==1,也就是在第一轮epoch中,保存了一个batch_size=100的图片。你能区分那个是真实数据,那个是真实数据吗,左边是通过训练200轮生成的图片,右边是真实数据,怎么样,效果还不错。
我有个习惯一般训练好的模型,如果我要应用起来,是一定需要部署的,而这个最基础的第一步就是模型推理。
import os
import torch
import torchvision
import torch.nn as nn
from torchvision import transforms
from torchvision.utils import save_image
# ================================================================== #
# 可以说GD分类器训练完毕后就是完全独立的两个模型,可以分别进行推理使用,
# 一般我们需要使用的不是分辨网络,而是生成器,所以在这里我只弄了Generator推理,
# 如果有需要,也可以很好写Discriminator的推理,不会可以下方评论
# ================================================================== #
# Hyper-parameters
latent_size = 64
hidden_size = 256
image_size = 784
num_epochs = 200
batch_size = 100
sample_dir = 'samples'
# Device configuration
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model_path = "G.ckpt"
def denorm(x):
out = (x + 1) / 2
return out.clamp(0, 1)
# ================================================================== #
# 像素值出现在(-1,1)的原因是:
# transforms.ToTensor()将图片归一化到(0,1)
# transforms.Normalize([0.5, 0.5, 0.5], [0.5, 0.5, 0.5])])将图片归一化到(-1,1)#
# ================================================================== #
# Generator
G = nn.Sequential(
nn.Linear(latent_size, hidden_size),#64->256
nn.ReLU(),
nn.Linear(hidden_size, hidden_size),#256->256
nn.ReLU(),
nn.Linear(hidden_size, image_size),#256->784
nn.Tanh())
# Device setting
G = G.to(device)
G.load_state_dict(torch.load(model_path))
#准备噪声
z = torch.randn(batch_size, latent_size).to(device)#高斯随机分布数据按生成模型输入的size给出
fake_images = G(z)
# Save sampled images
fake_images = fake_images.reshape(fake_images.size(0), 1, 28, 28)
save_image(denorm(fake_images), os.path.join(sample_dir, 'inference.png'))
参考资料
像素值出现在(-1,1)的原因是:
transforms.ToTensor()将图片归一化到(0,1)
transforms.Normalize([0.5, 0.5, 0.5], [0.5, 0.5, 0.5])])将图片归一化到(-1,1)
————————————————
版权声明:本文为CSDN博主「xzxz_123」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/weixin_44887621/article/details/120535309
图片保存:torchvision.utils.save_image(img, imgPath)
深度学习模型中,一般使用如下方式进行图像保存(torchvision.utils中的save_image()函数),
这种方式只能保存RGB彩色图像,如果网络的输出是单通道灰度图像,则该函数依然会输出
三个通道,每个通道的数值都是相同的,即“伪灰度图像”,虽然从视觉效果上看不出区别,
但是图像所占内存比正常情况大了两倍。
————————————————
版权声明:本文为CSDN博主「代码小白的成长」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/weixin_43723625/article/details/108159190可以看到,优化D的时候,也就是判别网络,其实没有生成网络什么事,后面的G(z)这里就相当于已经得到的假样本。优化D的公式的第一项,使的真样本x输入的时候,得到的结果越大越好,可以理解,因为需要真样本的预测结果越接近于1越好嘛。对于假样本,需要优化是的其结果越小越好,也就是D(G(z))越小越好,因为它的标签为0。但是呢第一项是越大,第二项是越小,这不矛盾了,所以呢把第二项改成1-D(G(z)),这样就是越大越好,两者合起来就是越大越好。 那么同样在优化G的时候,这个时候没有真样本什么事,所以把第一项直接却掉了。这个时候只有假样本,但是我们说这个时候是希望假样本的标签是1的,所以是D(G(z))越大越好,但是呢为了统一成1-D(G(z))的形式,那么只能是最小化1-D(G(z)),本质上没有区别,只是为了形式的统一。之后这两个优化模型可以合并起来写,就变成了最开始的那个最大最小目标函数了。
所以回过头来我们来看这个最大最小目标函数,里面包含了判别模型的优化,包含了生成模型的以假乱真的优化,完美的阐释了这样一个优美的理论。
————————————————
版权声明:本文为CSDN博主「on2way」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/on2way/article/details/72773771交叉熵(cross entropy)是深度学习中常用的一个概念,一般用来求目标与预测值之间的差距。以前做一些分类问题的时候,没有过多的注意,直接调用现成的库,用起来也比较方便。最近开始研究起对抗生成网络(GANs),用到了交叉熵,发现自己对交叉熵的理解有些模糊,不够深入。遂花了几天的时间从头梳理了一下相关知识点,才算透彻的理解了,特地记录下来,以便日后查阅。
————————————————
版权声明:本文为CSDN博主「史丹利复合田」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/tsyccnh/article/details/79163834案例带你学Pytorch系列(3)——GAN生成对抗网络//同款代码的讲解
https://blog.csdn.net/houhuipeng/article/details/90261299交叉熵(cross entropy)是深度学习中常用的一个概念,一般用来求目标与预测值之间的差距。
以前做一些分类问题的时候,没有过多的注意,直接调用现成的库,用起来也比较方便。
最近开始研究起对抗生成网络(GANs),用到了交叉熵,发现自己对交叉熵的理解有些模糊,
不够深入。遂花了几天的时间从头梳理了一下相关知识点,才算透彻的理解了,特地记录下来,
以便日后查阅。
————————————————
版权声明:本文为CSDN博主「史丹利复合田」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/tsyccnh/article/details/79163834