PART 4 描述性统计分析
总体要求
理解统计基本概念、理解描述性统计相关只是内容、理解描述性统计图表定义及适用场景、能够应用描述性统计知识描述及探索业务问题
1、统计基本概念
1.1 统计学含义及其应用【熟知】
1.1.1 含义
统计学是一门收集、处理、分析、理解数据并从数据中心得出结论的科学
1.1.2 统计学分析步骤
收集数据→处理数据→分析数据（描述性统计分析、推理性统计分析）→解释数据
1.1.3 统计学分析数据的方法
- 描述性分析
研究数据收集、处理和描述的统计学方法
总体规模、对比关系、集中趋势、离散程度、偏态、峰态、……
- 推断性分析
研究如何利用样本数据来推断总体特征的统计学方法
估计、假设检验、列联分析、方差分析、相关分析、回归分析、……
1.1.4 统计学应用
随着计算机的发展及各种统计软件的开发，作为一门基础学科的统计学在金融、保险、生物、经济等领域得到了广泛应用。
1.2 统计学的基本概念【熟知】
1.2.1 数据
统计学的对象是数据。
-
数据的形式
数字：可以进行比较、加减乘除等运算，严格的数据符号，常用阿拉伯数字表示
文字：不可运算，如男、女等
- 数据的分类
| 按照计量尺度分类 | 概念 | 举例 | 是否可排序 | 是否可计算 | 数据类型 | 等级 |
| 分类型数据 | 对事物进行分类的结果 | 国籍、性别 | × | × | 定性数据 | 低级 |
| 顺序型数据 | 对事物类别顺序的测度 | 产品等级、健康等级 | √ | × | 定性数据 | 中级 |
| 数值型数据 | 对事物的精确测度 | 身高、体重 | √ | √ | 定量数据 | 高级 |
- 数据的其他分类
| 分类角度 | 类别 | 举例 |
| 按来源不同 | 直接来源（一手数据、原始资料） | 亲自梳理 |
| 间接来源（二手数据、次级资料） | 从别人的结果挖出来 | |
| 按收集方式不同 | 观测的数据 | 没办法控制变量，所见即所得。如观测居民收入情况，没办法控制其他变量 |
| 实验的数据 | 可以控制其他变量。如测量药品是否有效，可以控制体温、血压等其他变量 | |
| 按与时间的关系不同 | 截面数据 | 在一个时间点或一个时间段取到的数据。如企业上个月的数据 |
| 时间序列数据 | 跟着时间会发生变化的数据，其特点是过去会影响今天，今天会影响未来。如股票 | |
| 混合数据（面板数据） | 即含有时间属性，又含有空间属性的数据。如企业去年一年（时间）在全国各个省市（空间）的销量 | |
| 按概型不同 | 离散型数据 | 如卖出去商品的个数 |
| 连续性数据 | 如时间，可以无限细分 | |
| 一种特殊的数据 | 虚拟变量数据 | 如教育水平、产品质量 |
1.2.2 总体和样本
- 总体（population）
指研究的所有元素的集合，其中每个元素成为个体。
如：现研究全校学生的平均年龄，总体是：全校学生和总体相关的事物，统计学上用希腊字母表示。
- 样本（sample）
从总体中抽取的一部分元素的集合。
如：为研究全校学生的平均年龄，由于总体太大，从中抽取100人进行研究，该研究中的样本是抽取的这100个学生。
和样本相关的事物，统计学生用英文字母表示。
构成样本的元素的数目称为样本容量。
所有和总体有关的东西都是一个定值，所有和样本有关的东西都是一个变量。
1.2.3 参数和统计量
- 参数（parameter）
指研究者想要了解的总体的某种特征值
主要有总体均值（
）、总体标准差（
）、总体比例（
）等
- 统计量（statistics）
指根据样本数据计算出来的一个量，即样本的某个特征值；
常见的统计量有样本均值（
）、样本标准差（s）、样本比例（p）等。
1.2.4 变量
- 变量
指描述事物某种特征的概念。如商品销售额、受教育程度、产品的质量等级等。
- 变量与数据的关系
变量的具体表现称为变量值，即数据。
- 变量的分类
根据变量的数据计量尺度不同来分
分类变量（categorical variable）：说明事物类别的一个名称
顺序变量（rank variable）：说明事物有序类别的一个名称
数值型变量（metric variable）：说明事物数字特征的一个名称
2、数据的描述性统计
2.1 描述性统计图表【领会】
2.1.1 直方图
定义：由一系列高度不等的巨型表示数据分布的情况。
- 频数分布直方图
定义：在统计数据时，横轴按组距分类，纵轴表示频数，每个矩阵的高代表对应组距里数据的频数，称这样的统计图为频数分布直方图。
组数：把数据按照不同的范围分成几个组，分成的组的个数称为组数。
组距：每一组数据的极差。
特点：
a.能够显示各组频数分布的情况
b.易于显示各组之间频数的差别
- 绘制直方图
- 收集数据。作直方图的数据一般大于50个
- 选择数据列，插入图表：直方图
- 确定数组、极差、组距
- 绘制注意事项
- 抽取的样本数量过小，将会产生较大的误差，可信度低，也就失去了统计的意义。因此，样本数不应少于50个。
- 组数选用不当，偏大或偏小，都会造成对分布状态的判断有误。
2.1.2 散点图
定义：梳理统计分析中，数据点在平面直角坐标系上的分布图，表示因变量随自变量而变化的大致趋势。
特点：
- 展示数据的分布情况
- 发现变量之间的关系
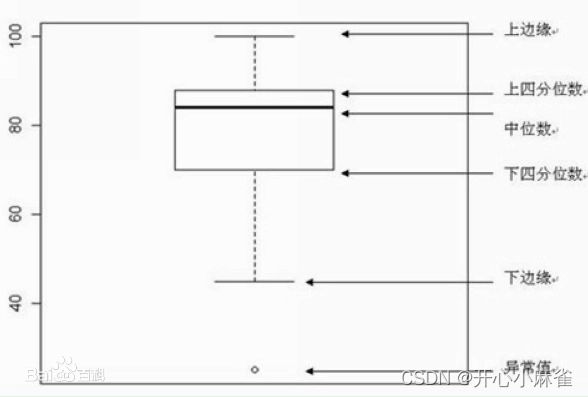
2.1.3 箱型图
又称为盒须图或箱线图，显示一组数据分散情况的统计图
2.2 集中趋势的描述——平均指标【领会】
集中趋势（Central tendency）：一组数据向其中心值靠拢的趋势
测度集中趋势就是寻找数据水平的代表值或中心值
-
各类型数据可用指标
分类型数据可用 众数
顺序型数据可用 众数、分位数
数值型数据可用 众数、分位数、均值
2.2.1 众数
定义：出现次数最多的变量值
表示的符号：
计算：寻找数据中出现次数最多的值（众数的不唯一性）
2.2.2 分位数
定义：指根据对数据位置进行划分，处于某些特定位置上的数，常用的分位数有二分位数（也叫“中位数”）、四分位数、十分位数、百分位数等
- 中位数（二分位数）
定义：数据排序后，处于中间位置上的值
表示的符号：
计算：数据的个数为n，则中位数的位置=
（偶数个数据的中位数为中间两数平均值，奇数个数据的中位数为最中间的数值）
- 四分位数
定义：分为下四分位数和上四分位数两种，指排序后处于25%和75%位置上的值
表示的符号：下四分位数
，上四分位数
计算：数据的个数为n，则
下四分位数的位置：
上四分位数的位置：
2.2.3 均值（mean）
- 算术平均数
定义：数据的和与数据个数之比
表示的符号：
计算：
简单算术平均数（根据未分组数据计算的）：
加权算术平均数（根据分组数据计算的）：
（其中：数据个数为n，分组数据的组数为k，
为组中值，
为各组的频数，每一组的权重为
。）
特点：易受极端值影响
- 几何平均数
定义：n个变量值乘积的n次方根
表示的符号：G
计算：
简单几何平均数（根据未分组数据计算的）：G=![\sqrt[n]{x_{1}x_{2}...x_{n}}](http://img.e-com-net.com/image/info8/ba6a838944594527b603f9e9955f498d.gif){kind=small}
加权几何平均数（根据分组数据计算的）：G=![\sqrt[(f1+f2+...+fn)]{x_{1}^{f1}x_{2}^{f2}...x_{n}^{fn}}](http://img.e-com-net.com/image/info8/509604e433904ceab88e97d9bef2808d.gif){kind=small}
（其中，数据个数为n，分组数据的组数为k，为组中值，为各组的频数。）
特点：
a.易受极端值影响
b.常用于增长率数据的研究（如利率）
c.所有数据需大于0
- 调和平均数
定义：变量值倒数的算数平均数的倒数
表示的符号：H
计算：
简单调和平均数（根据未分组数据计算的）：
加权调和平均数（根据分组数据计算的）：
（其中：数据个数为n，分组数据的组数为k，为组中值，为各组的频数。）
特点：
a.易受极端值影响
b.常用于效率数据的研究
c.有一项为0就无法计算H
- 均值不等式
对于同一组数据，一定满足：算术平均数≥几何平均数≥调和平均数
当所有数据取值相同的时候，等号成立。
2.3 离散程度的描述——变异指标【领会】
- 离散程度：
定义：反映各变量远离其中心值的程度，是数据分布的另一个重要特征
从另一个侧面说明了集中趋势测试度值的代表程度
2.3.1 极差（range）
定义：一组数据的最大值与最小值之差
表示的符号：R
计算：R=max(
)-min()
特点：
a.离散程度的最简单测度值
b.极易受极端值影响
c.未考虑数据的分布
2.3.2 平均差（mean deviation）
定义：各变量值与其均值离差绝对值的平均数
表示的符号：
计算：
未分组数据：
分组数据：
(为组中值)
特点：
a.能全面反映一组数据的离散程度：越大，表示数据越分散。
b.数学性质较差，实际中应用较少
2.3.3 方差和标准差
- 根据总体数据计算的，称为总体方差、总体标准差；
- 根据样本数据计算的，称为样本方差、样本标准差；
定义：变量值与其算术平均数的离差的平方的算术平均数
表示的符号：
总体方差：
总体标准差：
样本方差：
样本标准差：s
计算：
-
总体方差
未分组数据：
分组数据：
(为组中值)
- 总体标准差：
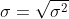
- 样本方差
未分组数据：
分组数据：
（为组中值）
- 样本标准差：
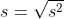
注：样本方差计算公式的分母是n-1
- 样本方差自由度（degree of freedom）
- 自由度是指一组数据中可以自由取值的数据的个数
特点：
a.数据离散程度的最常用测量度值
b.反映了各变量值与均值的平均差异：方差或标准差越大，表示变量值与均值的平均差异越大
2.3.4 离散系数（变异系数）
定义：是标准差与均值之比
表示的符号：
计算：
特点：
a.是对数据相对离散程度的测度
b.消除了数据水平不同和数据计量单位不同对数据离散程度的影响
c.常用于对不同组别数据离散程度的比较
2.4 分布形态的描述——偏态与峰态【领会】
2.4.1 偏态（skewness）
定义：是指数据分布偏斜程度。
测量方法：使用偏态系数来测度数据的偏态。偏态系数用符号SK表示。
偏态系数的计算：（公式有多种，这里选常见的一种）
未分组数据：
分组数据：
偏态的判断：
- SK=0对称分布；SK>0右偏分布；SK<0左偏分布
- 偏态的程度
低度偏态分布：0<|SK|≤0.5
中等偏态分布：0.5<|SK|≤1
高度偏态分布：|SK|＞1
- 偏态对众数、中位数和均值之间关系的影响
对称分布：均值=中位数=众数
左偏分布：均值＜中位数＜众数
右偏分布：众数＜中位数＜均值
2.4.2 峰态（kurtosis）
定义：是指数据分布的扁平程度。
测量方法：使用峰态系数来测度数据的峰态。峰态系数用符号K表示。
峰态系数的计算：（公式有多种，这里选常见的一种）
未分组数据：
分组数据：
峰态的判断：K=0扁平峰度适中 K＞0尖峰分布 K＜0扁平分布
峰态的程度：
低度尖峰分布：0<|K|≤0.5
中等尖峰分布：0.5<|K|≤1
高度尖峰分布：|K|>1
2.5 总体规模的描述——总量指标
反映在一定时间、空间条件下某种现象的总体规模、总水平或总成果的统计指标。如：营业额、利润
2.6 对比关系的描述——相对指标
是两个有相互联系的指标数值之比。
如：目标完成率（实际完成/计划完成）
【应用】能够应用描述性统计知识对业务数据进行恰当的数据特征描述，针对数据描述特征阐述业务问题、探索问题原因、提出解决问题的方法