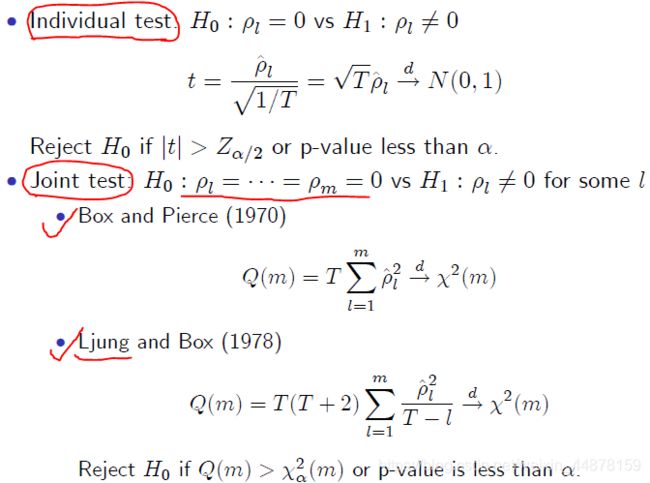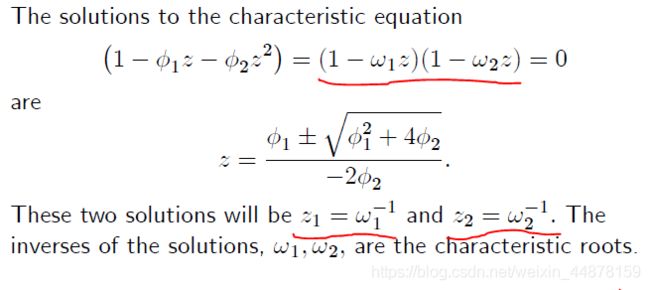统计 | 时间序列学习笔记

（所有ppt截图，以及部分代码，来自中财黄白老师的ppt）

一、复习

Lecture 1、2

1、损失函数与最优一步预测

• 一个随机过程：$Z_t\equiv {\left(Y_t,X_t^{\prime }\right)}^{\prime }$，$X_t$是一个向量，$Y_t$是我们感兴趣的变量
• 我们可以利用T期观测：$\left\{Z_1,\dots ,Z_t\right\}$，来估计模型参数${\hat{\beta }}_t$
• 由此得到一步预测：$f\left(Z_t,{\hat{\beta }}_t\right)$令$f_{t,1}\equiv f\left(Z_t,{\hat{\beta }}_t\right)$，用$f_{t,1}$来估计$Y_{t+1}$
• 一步预测误差：$e_{t+1}\equiv Y_{t+1}-f_{t,1}$
• 一步预测误差的损失函数：$c\left(e_{t+1}\right)$，最优预测$f_{t,1}^{\ast }$使得损失函数能够达到最小：$$f_{t,1}^{\ast }=arg\underset{f_{t,1}}{\min }{\int }_{-\infty }^{\infty }c\left(y-f_{t,1}\right)d{F}_t(y)$$
  则最优预测误差：$e_{t+1}^{\ast }=Y_{t+1}-f_{t,1}^{\ast }$
• 求$f_{t,1}^{\ast }$的过程：
  令偏导数等于0，$$\frac{\partial }{\partial f_{t,1}}{\int }_{-\infty }^{\infty }c\left(y-f_{t,1}^{\ast }\right)d{F}_t(y)=0$$ 当积分和求导符号互换时，$$\begin{array}{rl}& {\int }_{-\infty }^{\infty }\frac{\partial }{\partial f_{t,1}}c\left(y-f_{t,1}^{\ast }\right)d{F}_t(y)\equiv E\left(\frac{\partial }{\partial f_{t,1}}c\left(Y_{t+1}-f_{t,1}^{\ast }\right)|I_t\right)\\ & \equiv E\left(g_{t+1}|I_t\right)=0\end{array}$$ 其中，$I_t=\left\{Z_1,\dots ,Z_t\right\}$， $g_{t+1}\equiv \frac{\partial }{\partial f_{t,1}}c\left(Y_{t+1}-f_{t,1}^{\ast }\right)$

2、平方损失函数

• 平方损失函数：$c\left(Y_{t+1}-f_{t,1}\right)\equiv {\left(Y_{t+1}-f_{t,1}\right)}^2$. 所以$g_{t+1}\equiv \frac{\partial }{\partial f_{t,1}}c\left(Y_{t+1}-f_{t,1}^{\ast }\right)=-2e_{t+1}^{\ast }$，那么$$E\left(e_{t+1}^{\ast }|I_t\right)=0$$所以，$E\left(Y_{t+1}-f_{t,1}^{\ast }|I_t\right)=0$，即$$f_{t,1}^{\ast }=E\left(Y_{t+1}|I_t\right)$$

另外，在check loss下，$f_{t,1}^{\ast }=q_{\alpha }\left(Y_{t+1}|I_t\right)$

3、平稳性的定义

• 严平稳（Strictly stationarity）：$\{X_t\}$为一时间序列，$对于任意的m，$\tau$，有$$F_{t_1,t_2,,...,tm}(x_1,x_2,...,x_m)=F_{t_1+\tau ,t_2+\tau ,...,t_m+\tau }(x_1,x_2,...,x_m)$$联合概率分布相等
• 宽平稳（Covariance stationarity）：若时间序列满足$\{X_t\}$以下条件，
  (1)一阶原点矩存在，$E{X}_t=\mu$，$\mu$为常数
  (2)二阶原点矩存在，$E{X}_t^2<\infty$
  (3)协方差至于时间间隔有关，$\gamma (t,s)=\gamma (k,k+s-t)$
  则该时间序列是宽平稳的。又称弱平稳或二阶平稳（second-order stationary、wide-sense stationarity、weak stationarity）。

对于一个时间序列$\{X_t\}$
（1）均值${\mu }_t$
（2）协方差$\gamma (t,s)=cov(X_t,X_s)=\mathbb{E}\left(X_t-{\mu }_t\right)\left(X_s-{\mu }_s\right)$

注：严平稳和宽平稳不能互相推断
虽然严平稳比宽平稳的条件更严格，但二者不能互相推断。

• 严平稳的时间序列不一定是宽平稳的。如：服从柯西分布的严平稳序列，不存在一阶、二阶矩，所以不是宽平稳的。只有二阶矩存在的严平稳序列才是宽平稳的。
• 宽平稳的时间序列也不一定是严平稳的。只有时间序列$\{X_t\}$是正态时间序列时，宽平稳才能推出严平稳。

正态时间序列
一个随机时间序列$\{X_t\}$，若对于任意时间$(t_1,...,t_n)$，$(x_{t_1},...,x_{t_n})$满足联合正态分布，那么这个时间序列是正态时间序列。

3、遍历性

时间序列可以被研究，需要具有一些性质：遍历性和平稳性

• Ensemble average：
  随机过程$\left\{X\left({\omega }_i,t\right),t=1,\dots ,n\right\}$的某一个样本路径$\left\{x_1^{(i)},x_2^{(i)},\dots x_n^{(i)}\right\}$，即$x_t^{(i)}=X\left({\omega }_i,t\right)$。均值$\mu =E(X_t)$可以被ensemble averages${\hat{\mu }}_t=k^{-1}{\sum }_{i=1}^k{X}_t^{(i)},t=1,\dots ,n$所估计

事实上，i只有一个。

人不能同时踏进两条河流。

• time average：实际上，我们只有$\left\{x_1^{(1)},x_2^{(1)},\dots x_n^{(1)}\right\}$对于${\omega }_1$。因为时间序列的平稳性有：${\mu }_t=\mathbb{E}(X_t)=\mu$，我们用time average${\bar{x}}_n=n^{-1}{\sum }_{t=1}^n{x}_t^{(1)}$来估计$\mu$
• 均值的遍历性（ergodicity）：如果time average收敛于常数均值，${\bar{x}}_n{\to }^p\mu$，那么我们称该时间序列式均值遍历的。

4、经济模型

CAPM

• 资本资产定价模型(Capital Asset Pricing Model)$$\mathbb{E}\left(R_p-r_f\right)=\beta \mathbb{E}\left(R_m-r_f\right)$$也可以被写成
  $$\mathbb{E}\left(R_p\right)=r_f+\beta \left(\mathbb{E}\left(R_m\right)-r_f\right)$$其中，$R_p$是投资组合的收益率，$r_f$是无风险利率，$\beta$是风险系数，$R_m$是市场收益率，${\mathbb{E}}_{(}{R}_m)-r_f$表示风险溢价。
  根据最小二乘法，可以得到：$$\beta =\frac{\mathrm{cov}\left(R_p-r_f,R_m-r_f\right)}{\mathrm{var}\left(R_m-r_f\right)}=\frac{{\sigma }_{XY}}{{\sigma }_X^2}$$
  $\beta$与相关系数$\rho =\frac{{\sigma }_{XY}}{{\sigma }_X{\sigma }_Y}=\beta \frac{{\sigma }_X}{{\sigma }_Y}$有关。
• 意义：
  1.任何风险性资产的预期报酬率=无风险利率+资产风险溢酬。
  2.资产风险溢酬=风险的价格×风险的数量
  3.风险的数量 = β
  4.风险的价格 = $E(R_m)-r_f$

HM

• 无条件均值模型：$\mathbb{E}\left(R_{it}\right)={\mu }_i$，有时也被称为 HM模型(Historical Mean Model)。对于某一资产i，我们有：$$R_{it}=\mathbb{E}\left(R_{it}\right)+{\xi }_{it}={\mu }_i+{\xi }_{it}$$ $$\mathbb{E}\left({\xi }_{it}\right)=0,\mathrm{Var}\left({\xi }_{it}\right)={\sigma }_{{\xi }_i}^2$$其中，${\xi }_{it}$被称作不正常回报，$R_{it}$被称为名义收益或额外收益，回归的决定系数$R^2=0$

Market Model

• 条件均值模型：$\mathbb{E}\left(R_{it}|R_{mt}\right)={\alpha }_i+{\beta }_i{R}_{mt}$。对于某项资产i来讲，$$R_{it}=\mathbb{E}\left(R_{it}|R_{mt}\right)+{\epsilon }_{it}={\alpha }_i+{\beta }_i{R}_{mt}+{\epsilon }_{it}$$ $$\mathbb{E}\left({\epsilon }_{it}\right)=0,\mathrm{Var}\left({\epsilon }_{it}\right)={\sigma }_{{\epsilon }_i}^2$$回归的决定系数为$R^2=1-\frac{{\sigma }_{{\epsilon }_i}^2}{{\sigma }_{{\xi }_i}^2}$，所以${\sigma }_{{\epsilon }_i}^2=\left(1-R^2\right){\sigma }_{{\xi }_i}^2\le {\sigma }_{{\xi }_i}^2$

setwd("D:/data")
library(fBasics)#时间序列一个重要的包
da = read.table("m-ibm6708.txt",header = T)#读到一个data.frame里
da[1,]
ibm = da$ibm

#Constane Mean Return Model
stdev(ibm)#因变量的标准差

#Market Model
sp = da$sprtn
plot(sp,ibm)
cor(sp,ibm)
marketmodel = lm(ibm~sp)
marketmodel
summary(marketmodel)

相关性
Pearson相关系数不适用描述非线性相关性、不适用于描述分布非正态的随机变量间的相关、对于异常点不具有稳健性。
其他几种相关系数：
1、Spearman’s rank correlation
2、Pseudo correlation
3、Kendall’s $\tau$
注：如果X和Y满足联合正态分布，则他们之间的Pearson’s $\rho$ = Spearman’ rank correlation = Pseudo correlation

#Measure of Correlation and Dependence
cor(sp,ibm)    #pearson's correlation
cor(sp,ibm,method = "spearman")#Spearman's rank correlation
cor(rank(sp),rank(ibm))        #Spearman's rank correlation
cor(sp,ibm,method = "kendall")#Kendall's tau

#invariance to monotonic nonlinear transformation
cor(exp(sp),exp(ibm))                   #not invariant
cor(exp(sp),exp(ibm),method = "spearman")#invaraint
cor(rank(exp(sp)),rank(exp(ibm)))
cor(exp(sp),exp(ibm),method = "kendall")#invaraint

有效市场假说

二、ARMA

1、基本概念

• 均值和方差：$\mu =\mathbb{E}\left(r_t\right)$，$\mathrm{Var}\left(r_t\right)=\mathbb{E}\left[{\left(r_t-\mu \right)}^2\right]$
  自协方差：${\gamma }_l=\mathrm{Cov}\left(r_t,r_{t-l}\right)=\mathbb{E}\left(r_t-\mu \right)\left(r_{t-l}-\mu \right)$
  自相关系数：${\rho }_l=\frac{\mathrm{Cov}\left(r_t,r_{t-l}\right)}{\mathrm{Var}\left(r_t\right)}=\frac{{\gamma }_l}{{\gamma }_0}$
• 样本均值和样本方差：${\bar{r}}_T=\frac{1}{T}{\sum }_{t=1}^T{r}_t$，$s_T^2=\frac{1}{T-1}{\sum }_{t=1}^T{\left(r_t-\bar{r}\right)}^2$
  样本自相关系数（ACF）：${\hat{\rho }}_l=\frac{{\sum }_{t=l+1}^T\left(r_t-{\bar{r}}_T\right)\left(r_{t-l}-{\bar{r}}_T\right)}{{\sum }_{t=1}^T{\left(r_t-{\bar{r}}_T\right)}^2}$

相关系数是否为0的假设检验：

2、AR模型

---

• AR(1)
  模型：$$r_t={\varphi }_0+{\varphi }_1{r}_{t-1}+a_t$$或
  $$\left(1-{\varphi }_{1}B\right)r_t={\varphi }_0+a_t$$
  平稳性条件：当且仅当$|{\varphi }_1|<1$时（充分必要条件），AR(1)平稳

当所有特征根在单位圆外时，AR模型平稳

均值：$\mu =\mathbb{E}\left(r_t\right)=\frac{{\varphi }_0}{1-{\varphi }_1}$
（所以得到AR(1)的另一种表达：$\left(r_t-\mu \right)={\varphi }_1\left(r_{t-1}-\mu \right)+a_t$）
方差：$\mathrm{Var}\left(r_t\right)=\frac{{\sigma }_a^2}{1-{\varphi }_1^2}$
自相关系数：${\rho }_1={\varphi }_1,{\rho }_2={\varphi }_1^2,\dots ,{\rho }_k={\varphi }_1^k$

一步预测：${\hat{x}}_n(1)={\varphi }_1{x}_n$
一步预测误差：$e_n(1)=x_{n+1}-{\hat{x}}_n(1)=a_{n+1}$
一步预测误差的方差：$\mathrm{Var}\left[e_n(1)\right]=\mathrm{Var}\left(a_{n+1}\right)={\sigma }_a^2$

两步预测：${\hat{x}}_n(2)={\varphi }_1{\hat{x}}_n(1)={\varphi }_1^2{x}_n$
两步预测误差：$e_n(2)=x_{n+2}-{\hat{x}}_n(2)=a_{n+2}+{\varphi }_1{a}_{n+1}$
一步预测误差的方差：$\mathrm{Var}\left[e_n(2)\right]=\left(1+{\varphi }_1^2\right){\sigma }_a^2$

k步预测：${\hat{x}}_n(l)={\varphi }_1^l{x}_n$
k步预测误差：$e_n(l)=a_{n+l}+{\varphi }_1{a}_{n+l-1}+\cdots +{\varphi }_1^{l-1}{a}_{n+1}$
k步预测误差的方差：$\mathrm{Var}\left[e_n(l)\right]=\left(1+{\varphi }_1^1+\cdots +{\varphi }_1^{2(l-1)}\right){\sigma }_a^2$

---

• AR(2)
  模型：$$r_t={\varphi }_0+{\varphi }_1{r}_{t-1}+{\varphi }_2{r}_{t-2}+a_t$$也可以写成$$\left(1-{\varphi }_{1}B-{\varphi }_2{B}^2\right)r_t={\varphi }_0+a_t$$
  平稳性条件：当特征方程$\left(1-{\varphi }_{1}z-{\varphi }_2{z}^2\right)=0$的所有跟位于单位圆外时，AR(2)平稳

均值：$\mathbb{E}\left(r_t\right)=\frac{{\varphi }_0}{1-{\varphi }_1-{\varphi }_2}$
自相关系数：${\rho }_0=1$，${\rho }_1=\frac{{\varphi }_1}{1-{\varphi }_2}$，${\rho }_l={\varphi }_1{\rho }_{l-1}+{\varphi }_2{\rho }_{l-2}$ (for l>2)

3、MA模型

---

• MA(1)
  == 模型==：$r_t=\mu +a_t-\theta a_{t-1}$
  平稳性：MA模型总是平稳的
  可逆性：$|\theta |<1$
  均值：$\mathbb{E}\left(r_t\right)=\mu$
  方差：$\mathrm{Var}\left(r_t\right)=\left(1+{\theta }^2\right){\sigma }_a^2={\gamma }_0$
  自协方差：${\gamma }_1=\mathrm{Cov}\left(r_t,r_{t-1}\right)=-\theta {\sigma }_a^2$，${\gamma }_2=\mathrm{Cov}\left(r_t,r_{t-l}\right)=0$ for $l>1$
  自相关系数：${\rho }_1=\frac{{\gamma }_1}{{\gamma }_0}=\frac{-\theta }{1+{\theta }^2}$，${\rho }_l=0$ for $l>1$
  注：由自相关系数可以看出，MA模型两步及以上无记忆性

一步预测：${\hat{r}}_t(1)=\mu -\theta a_n$
一步预测误差：$e_n(1)=a_{n+1}$

多步预测：${\hat{r}}_n(l)=\mu$ for $l>1$
多步预测的误差：$e_n(l)=a_{n+l}-\theta a_{n+l-1}$
多步预测的误差的方差：$\left(1+{\theta }^2\right){\sigma }_a^2={\gamma }_0$

---

• MA(2)
  模型：$r_t=\mu +a_t+{\theta }_1{a}_{t-1}+{\theta }_2{a}_{t-2}=\mu +\left(1+{\theta }_{1}B+{\theta }_2{B}^2\right)a_t$（R语言）
  均值：$E\left(r_t\right)=\mu$
  方差：$\mathrm{Var}\left(r_t\right)=\left(1+{\theta }_1^2+{\theta }_2^2\right){\sigma }_a^2={\gamma }_0$$\mathrm{Var}\left(r_t\right)=\left(1+{\theta }_1^2+{\theta }_2^2\right){\sigma }_a^2={\gamma }_0$
  自相关系数：${\rho }_2\ne 0,$ but ${\rho }_l=0$ for $l>2$

多步预测：${\hat{r}}_n(l)=\mu$ for $l>2$
多步预测的方差：Variance of multi-step ahead forecast error is unconditional
variance of $r_t$

3、ARMA模型