模型效果评估指标(ROC、AUC/KS、Lift、PSI)
以二分类问题为例
混淆矩阵(Confusion Matrix)
对测试集数据进行预测,得到下列混淆矩阵中的数据

注:TP、FN、FP、TN以预测的结果是否准确来命名。
预测模型评估指标的本质是从模型预测结果出发来度量模型性能优劣的,如分类模型从混淆矩阵中得到各种不同的性能指标,回归模型直接从预测结果与真实结果的偏差角度进行分析。
根据混淆矩阵计算召回率(Recall)和精准率(Precision)指标
R e c a l l = T P T P + F N Recall = \frac{TP}{TP+FN} Recall=TP+FNTP
P r e c i s i o n = T P T P + F P Precision = \frac{TP}{TP+FP} Precision=TP+FPTP
召回率与精准率是一对相互制约、此消彼长(负相关)的指标,实际应用中往往会牺牲某一指标来提高另一指标。
Gain的计算公式和Precision是一样的。
F1指标
F 1 = 2 × P r e c i s i o n × R e c a l l P r e c i s i o n + R e c a l l F_1 = \frac{2\times Precision\times Recall }{ Precision+Recall } F1=Precision+Recall2×Precision×Recall
F1指标综合考虑了召回率与精准率两个指标。
如果希望考虑更多的召回率或精准率,这有如下的变异形式,即 F β F_\beta Fβ指标:
F β = ( 1 + β 2 ) × P r e c i s i o n × R e c a l l β 2 × P r e c i s i o n + R e c a l l F_\beta = \frac{(1+\beta ^2)\times Precision\times Recall }{ \beta^2\times Precision+Recall } Fβ=β2×Precision+Recall(1+β2)×Precision×Recall
当 β = 1 \beta=1 β=1时, F β F_\beta Fβ指标蜕化为 F 1 F_1 F1指标,此时召回率与精准率的重要程度相同;
当 β > 1 \beta>1 β>1时,召回率的影响大于精准率;
当 β < 1 \beta<1 β<1时,精准率的影响大于召回率;
通过率定义为模型判断为好样本的数量占总样本数的比例,如下:
通 过 率 = T P + F P T P + F P + T N + F N 通过率 = \frac{TP+FP}{TP+FP+TN+FN} 通过率=TP+FP+TN+FNTP+FP
错误率和正确率(精度)(Accuracy)
错 误 率 = F P + F N T P + F P + T N + F N 错误率 = \frac{FP+FN}{TP+FP+TN+FN} 错误率=TP+FP+TN+FNFP+FN
A c c = T P + T N T P + F P + T N + F N Acc = \frac{TP+TN}{TP+FP+TN+FN} Acc=TP+FP+TN+FNTP+TN
概率密度评估指标
IV值(K-L距离)
相对熵,也称为K-L散度,然而,K-L散度没有对称性,对称化后的K-L散度即K-L距离就是IV值。
概率分布评估指标
根据混淆矩阵计算真正率(TPR)和假正率(FPR)指标
T P R = T P T P + F N = R e c a l l TPR = \frac{TP}{TP+FN}=Recall TPR=TP+FNTP=Recall
F P R = F P F P + T N FPR = \frac{FP}{FP+TN} FPR=FP+TNFP
一、ROC曲线、AUC和KS
截断点:每个分类模型都有一个截断点
以真正率TPR为纵坐标,以假正率FPR为横坐标绘制的曲线就是ROC(Receiver Operating Characteristic)曲线,全称为受试者工作特征曲线。ROC曲线上每个点表示分类模型在特定的截断点下的(TPR、FPR)。ROC曲线越靠近左上角模型的表现越好。

AUC值
AUC(Area under the curve)值,即ROC曲线与坐标轴围成的面积,面积越大表示模型的性能越好。AUC的取值范围为0~1之间,AUC的值存在小于0.5的情况,不过AUC的值要大于0.5才有意义。一般来说AUC大于0.75的模型效果表现较好。AUC越接近1,说明预测效果越好。

AUC = A + C = A + 0.5
| AUC值 | 模型性能 |
|---|---|
| 0.5 < A U C < 0.6 0.5 < AUC<0.6 0.5<AUC<0.6 | 区分能力较低 |
| 0.6 ⩽ A U C < 0.75 0.6 \leqslant AUC<0.75 0.6⩽AUC<0.75 | 区分能力中等 |
| 0.75 ⩽ A U C < 1 0.75 \leqslant AUC<1 0.75⩽AUC<1 | 区分能力较高 |
KS值
计算方法为:
K S = m a x ( T P R − F P R ) KS = max(TPR-FPR) KS=max(TPR−FPR)
KS值反应了模型对正负样本的区分能力,KS值越大表示对好坏样本的区分能力越强,模型的性能越优,最大的KS值对应的概率即为预测模型的最优切分阈值(cutoff)点。
| KS值 | 模型性能 |
|---|---|
| k s < 0.1 ks<0.1 ks<0.1 | 没有区分能力 |
| 0.1 ⩽ k s < 0.25 0.1 \leqslant ks<0.25 0.1⩽ks<0.25 | 区分能力一般 |
| 0.25 ⩽ k s < 0.4 0.25 \leqslant ks<0.4 0.25⩽ks<0.4 | 区分能力中等 |
| 0.4 ⩽ k s < 0.7 0.4 \leqslant ks<0.7 0.4⩽ks<0.7 | 区分能力强 |
| 0.7 ⩽ k s 0.7 \leqslant ks 0.7⩽ks | 区分能力太过 |
注意:KS值表征的是模型对正负样本的区分能力,但KS值本身没有倾向性,即对正样本区分好一些还是对负样本好一些,其KS值可能是一样的。因此,在实际使用过程中不能单看KS值这一单个指标,不能认为KS值很高,就断言模型可用。此时需要查看Recall和Precision,衡量模型对正样本的区分能力的好坏。
二、Lift提升度
Lift提升度(指数)衡量的是评分模型对坏样本的预测能力与不利用模型随机选择相比,模型的预测能力“变好”了多少倍,变好的倍数就是Lift,Lift越大,模型的效果越好,LIFT大于1说明模型表现优于随机。
l i f t = T P T P + F P P P + N lift = \frac{\frac{TP}{TP+FP}}{\frac{P}{P+N}} lift=P+NPTP+FPTP
Lift具体计算可以参考https://zhuanlan.zhihu.com/p/91223667
例如,不使用模型,采用随机粗放式的营销方式,客户转化成功率为1%,而使用模型进行精准营销,客户转化成功率为10%,那么lift = 10%/1% = 10
Gain是描述整体精准度的指标,在模型预测是Positive的样本中,模型预测正确的比例,这个比例也是越大越好,在0~1之间。
G a i n = T P T P + F P Gain = \frac{TP}{TP+FP} Gain=TP+FPTP
计算公式和精准率(Precision)的计算一样。
三、模型稳定性PSI
由于模型是以特定时间段的建模样本开发的,此模型是否适用于开发样本之外的样本(时间段不同或客群不同),必须经过稳定性测试才能得知。稳定度指标(population stability index ,PSI)可衡量测试样本和建模样本评分的分布差异,为最常见的模型稳定度评估指标。其实PSI表示的就是按分数分档后,针对不同客群样本,或者不同时间的样本,population分布是否有变化,就是看各个分数区间内样本占总样本的占比是否有显著变化。
P S I = ∑ ( a c t u a l − e x c e p t ) l n ( a c t u a l e x c e p t ) PSI = \sum(actual-except) ln\left(\frac{actual}{except}\right) PSI=∑(actual−except)ln(exceptactual)
PSI始终大于等于0,PSI越小,模型越稳定。
| PSI值 | 模型性能 |
|---|---|
| P S I < 0.1 PSI<0.1 PSI<0.1 | 样本分布有微小变化 |
| 0.1 ⩽ P S I < 0.2 0.1 \leqslant PSI<0.2 0.1⩽PSI<0.2 | 样本分布有变化 |
| P S I > 0.2 PSI>0.2 PSI>0.2 | 样本分布有显著变化 |
一般PSI小于0.25意味着变化在可接受范围内。
PSI既可以评估模型整体的稳定性,也可以评估特征的稳定性。
四、Gini系数
Gini系数经济学中用来评估收入分配公平程度,Gini系数具体指绝对公平线(Line of Equality)和洛伦茨曲线(Lorenz Curve)围成的面积与绝对公平线以下面积的比值,即Gini Coefficient = A面积/( A面积 + B面积)

用来评判分类预测模型的预测效果时,是指ROC曲线和中线围成的面积与中线之上面积的比值。

Gini = A /(A + B)= (AUC - C)/(A + B)=(AUC - 0.5)/ 0.5= (AUC-0.5) x 2 = 2AUC - 1
Gini系数与AUC是正相关的,且可以相互转换
宏平均(macro avg)和加权平均(weighted avg)
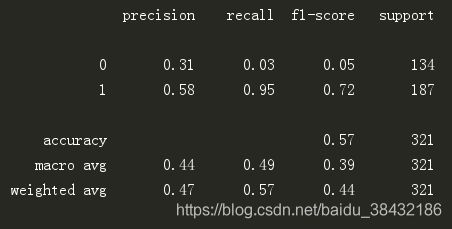
1、宏平均(macro avg)
对每个类别的精准率、召回率和F1加和,然后求平均
precision:macro avg = (P_0+P_1)/2=(0.31+0.58)/2 = 0.44
2、加权平均(weighted avg)
是对宏平均的一种改进,考虑了每个类别样本数量在总样本数量中的占比
precision:weighted avg = P_0*(support_0/support_all)+ P_1*(support_1/support_all = 0.31*(134/321) + 0.58*(187/321) = 0.47