Pytorch深度学习（二）

上一讲回顾

上一讲我们从零开始实现了Pytorch中的基本操作。

1. 首先从numpy中手写了基于最小loss（MSE）的线性回归程序（示例程序一）；
2. 然后从梯度下降的角度考虑，改写示例程序一，衍生成基于梯度下降的线性回归程序（示例程序二）；
3. 通过引入torch库函数，替换掉了原函数中的求梯度问题（采用.backward（）实现），完成了示例程序三；
4. 继续对示例程序三进行改写，定义了模型类，采用MSEloss以及SGD优化器，规范化了基于torch库的神经网络程序模型，整个模型框架分为四部分：
   4.1 准备数据集；
   4.2 设计模型类
   4.3 设计损失函数和优化器
   4.4 模型训练（forward, backward, update）
   完成了示例程序四；
5. 在示例程序四的基础上，针对二分类问题进行处理，定义评价函数为交叉熵$loss=-(ylog\hat{y}+(1-y)log(1-\hat{y}))$。Python程序中采用torch.nn.BCELoss，完成示例程序五
6. 在示例程序5中，添加多层神经网络串联，形成示例程序六。方法在构造模型类的时候，进行串联改写即可。
7. 示例程序七则考虑输入的数据集比较大，耗费内存的问题，引入batch的概念。方法是在准备数据集的部分定义class.详见示例程序。

下面继续：

该示例完成了手写数字识别的训练和测试，与之前的示例程序相比，该程序引入数据集与测试集（首次使用从网络上下载）。在测试集上不需要求梯度，with torch.no_grad():激活函数也改为了relu，计算Loss 采用CrossEntropyLoss（softmax）

import torch
from torchvision import  transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F 
import torch.optim as optim

batch_size = 64
transform = transforms.Compose([transforms.ToTensor(),
            transforms.Normalize((0.1307,),(0.3081 ))])

train_dataset = datasets.MNIST(root = '../dataset/mnist/',
                train=True,download=True,transform=transform)
train_loader = DataLoader(train_dataset,
                shuffle=True,batch_size=batch_size)
test_dataset = datasets.MNIST(root ='../dataset/mnist/',
                train=False,download=True,transform=transform)
test_loader = DataLoader(test_dataset,
                shuffle=False,batch_size=batch_size)

class Model(torch.nn.Module):  #继承于nn.Module
    def __init__(self):     #构造函数
        super(Model,self).__init__() #调用父类的构造
        self.linear1 = torch.nn.Linear(784,512)  #pytorch中的一个类，nn.linear,
        #继承于 Module 
        # 成员函数 weight,bias
        self.linear2 = torch.nn.Linear(512,256)
        self.linear3 = torch.nn.Linear(256,128)
        self.linear4 = torch.nn.Linear(128,64)
        self.linear5 = torch.nn.Linear(64,10)
        # self.sigmoid = torch.nn.Sigmoid()


    def forward(self,x):    #必须叫这个名字 ,父类中有forward这个函数
        #这个地方相当于override
        x = x.view(-1,784)
        x = F.relu(self.linear1(x))
        x = F.relu(self.linear2(x))
        x = F.relu(self.linear3(x))
        x = F.relu(self.linear4(x))
        # y_pred = torch.sigmoid(self.linear(x))
        return self.linear5(x)

model = Model()
epoch_list = []
loss_list = []
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr = 0.01, momentum = 0.5)  
            #  model.parameter()自动加载权重-all 权重  lr 自动学习率

def train(epoch):
    running_loss = 0.0
    for batch_idx,data in enumerate(train_loader,0):
        inputs, target = data
        optimizer.zero_grad()

        outputs = model(inputs)
        loss = criterion(outputs,target)
        loss.backward()
        optimizer.step()

        running_loss += loss.item()
        if batch_idx % 300 == 299:
            print('[%d, %5d] loss: %.3f' %(epoch+1,batch_idx+1,running_loss/300))
            running_loss = 0.0
def test():
    correct = 0
    total = 0
    with torch.no_grad():
        for data in test_loader:
            images, labels = data
            outputs = model(images)
            _,predicted = torch.max(outputs.data, dim=1)
            total += labels.size(0)
            correct += (predicted ==labels).sum().item()
    print('Accuracy on test set: %d %%' %(100*correct/total))
if __name__=='__main__':
    for epoch in range(10):
        train(epoch)
        test()

训练结果：

[1,   300] loss: 2.214
[1,   600] loss: 0.947
[1,   900] loss: 0.419
Accuracy on test set: 88 %
[2,   300] loss: 0.313
[2,   600] loss: 0.271
[2,   900] loss: 0.232
Accuracy on test set: 94 %
[3,   300] loss: 0.188
[3,   600] loss: 0.170
[3,   900] loss: 0.163
Accuracy on test set: 95 %
[4,   300] loss: 0.131
[4,   600] loss: 0.127
[4,   900] loss: 0.118
Accuracy on test set: 96 %
[5,   300] loss: 0.099
[5,   600] loss: 0.092
[5,   900] loss: 0.099
Accuracy on test set: 96 %
[6,   300] loss: 0.084
[6,   600] loss: 0.078
[6,   900] loss: 0.071
Accuracy on test set: 97 %
[7,   300] loss: 0.060
[7,   600] loss: 0.063
[7,   900] loss: 0.064
Accuracy on test set: 97 %
[8,   300] loss: 0.048
[8,   600] loss: 0.052
[8,   900] loss: 0.050
Accuracy on test set: 97 %
[9,   300] loss: 0.044
[9,   600] loss: 0.041
[9,   900] loss: 0.039
Accuracy on test set: 97 %
[10,   300] loss: 0.031
[10,   600] loss: 0.034
[10,   900] loss: 0.038
Accuracy on test set: 97 %

下面的例子考虑采用卷积神经网络以及池化层，并引入GPU来训练神经网络，这样CPU就再也不用100%满负荷跑了。

import torch
from torchvision import  transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F 
import torch.optim as optim

batch_size = 64
transform = transforms.Compose([transforms.ToTensor(),
            transforms.Normalize((0.1307,),(0.3081 ))])

train_dataset = datasets.MNIST(root = '../dataset/mnist/',
                train=True,download=True,transform=transform)
train_loader = DataLoader(train_dataset,
                shuffle=True,batch_size=batch_size)
test_dataset = datasets.MNIST(root ='../dataset/mnist/',
                train=False,download=True,transform=transform)
test_loader = DataLoader(test_dataset,
                shuffle=False,batch_size=batch_size)

class Model(torch.nn.Module):  #继承于nn.Module
    def __init__(self):     #构造函数
        super(Model,self).__init__() #调用父类的构造
        self.conv1 = torch.nn.Conv2d(1,10,kernel_size=5)
        self.conv2 = torch.nn.Conv2d(10,20,kernel_size=5)
        self.pooling = torch.nn.MaxPool2d(2)
        self.fc = torch.nn.Linear(320,10)
        # self.sigmoid = torch.nn.Sigmoid()


    def forward(self,x):    #必须叫这个名字 ,父类中有forward这个函数
        #这个地方相当于override
        batch_size = x.size(0)
        x = F.relu(self.pooling(self.conv1(x)))
        x = F.relu(self.pooling(self.conv2(x)))
        x = x.view(batch_size,-1)
        x = self.fc(x)
        # y_pred = torch.sigmoid(self.linear(x))
        return x

model = Model()
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
model.to(device)
epoch_list = []
loss_list = []
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr = 0.01, momentum = 0.5)  
            #  model.parameter()自动加载权重-all 权重  lr 自动学习率

def train(epoch):
    running_loss = 0.0
    for batch_idx,data in enumerate(train_loader,0):
        inputs, target = data
        inputs, target = inputs.to(device),target.to(device)
        optimizer.zero_grad()

        outputs = model(inputs)
        loss = criterion(outputs,target)
        loss.backward()
        optimizer.step()

        running_loss += loss.item()
        if batch_idx % 300 == 299:
            print('[%d, %5d] loss: %.3f' %(epoch+1,batch_idx+1,running_loss/300))
            running_loss = 0.0
def test():
    correct = 0
    total = 0
    with torch.no_grad():
        for data in test_loader:
            inputs, target = data
            inputs,target = inputs.to(device),target.to(device)
            outputs = model(inputs)
            _,predicted = torch.max(outputs.data, dim=1)
            total += target.size(0)
            correct += (predicted ==target).sum().item()
    print('Accuracy on test set: %d %%' %(100*correct/total))
if __name__=='__main__':
    for epoch in range(10):
        train(epoch)
        test()

[1,   300] loss: 0.649
[1,   600] loss: 0.203
[1,   900] loss: 0.145
Accuracy on test set: 96 %
[2,   300] loss: 0.109
[2,   600] loss: 0.101
[2,   900] loss: 0.094
Accuracy on test set: 97 %
[3,   300] loss: 0.078
[3,   600] loss: 0.076
[3,   900] loss: 0.076
[2,   900] loss: 0.094
Accuracy on test set: 97 %
[3,   300] loss: 0.078
[3,   600] loss: 0.076
[3,   900] loss: 0.076
Accuracy on test set: 98 %
[4,   300] loss: 0.067
[4,   600] loss: 0.064
[4,   900] loss: 0.062
Accuracy on test set: 98 %
[5,   300] loss: 0.051
[5,   600] loss: 0.065
[5,   900] loss: 0.051
Accuracy on test set: 98 %
[6,   300] loss: 0.050
[6,   600] loss: 0.050
[6,   900] loss: 0.048
Accuracy on test set: 98 %
[7,   300] loss: 0.047
[7,   600] loss: 0.045
[7,   900] loss: 0.045
Accuracy on test set: 98 %
[8,   300] loss: 0.040
[8,   600] loss: 0.043
[8,   900] loss: 0.041
Accuracy on test set: 98 %
[9,   300] loss: 0.040
[9,   600] loss: 0.038
[9,   900] loss: 0.038
Accuracy on test set: 98 %
[10,   300] loss: 0.035
[10,   600] loss: 0.035
[10,   900] loss: 0.039
Accuracy on test set: 98 %

可以看到准确率提高了。
后面，提出了梯度消失的问题（当神经网络层数逐渐增多之后），由于每层神经网络输出值在0~1之间，那么经过多次迭代之后，会出现梯度值接近0的情况，反馈之后造成前面的神经网络权重不在更新的情况。解决方法为引入 Residual Block 。

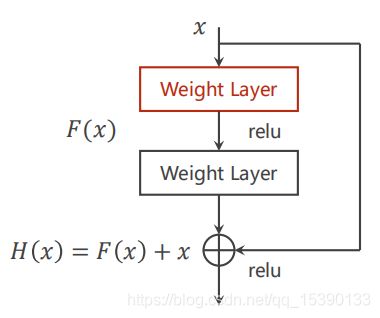
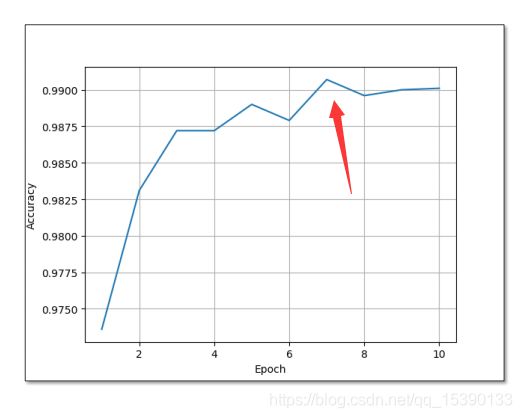
这个，在输出之后，就由原来在0附件，变成了在1附近变化，增加了前面神经网络的训练能力。具体代码就不在放了（本人不是图像专业，并没有进行实践，从老师给出的结果来看，准确度再次上升。达到99%），这里需要注意的是并不是网络层数越多越好，训练的轮数越多越好。这点需要通过实践训练看曲线得到。