决策树和随机森林算法原理和实现

决策树

概念

决策树是一种基本的分类与回归的方法。在机器学习中，经常用于解决分类问题，且有不错的效果。它是基于if-then的思想，对数据进行归类。

算法原理

决策树是选取数据中的特征，然后根据特征将训练样本切分，然后根据这个思想进行递归。决策树选取特征是通过信息熵和信息增益，选取信息增益较大的特征作为切分依据。

信息熵和信息增益

信息熵是指信息的不确定性的大小，信息熵越大说明信息的不确定性就越大。

信息熵的计算公式为
$$H(x)=-\sum _{i=1}^n{p}_{i}log{p}_i$$

而信息增益则是
$$g(D|A)=H(D)-H(D|A)$$

接下来举个例子，数据集如下，特征变量为：年龄情况、有无工作、有无房子、信贷情况

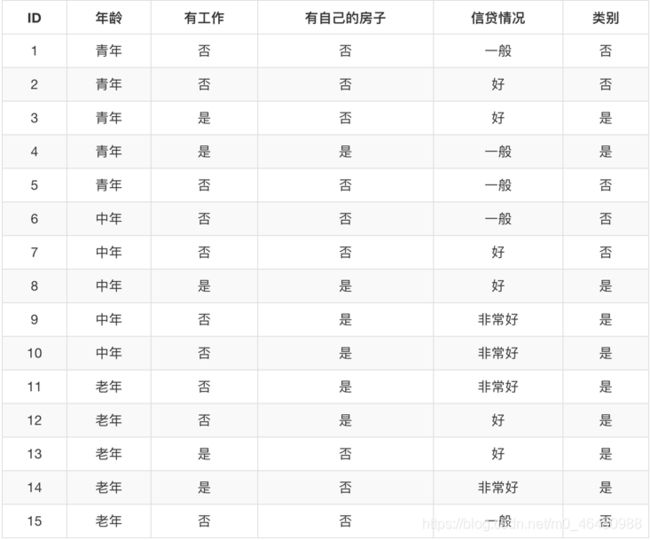
首先计算总的信息熵$H(D)$，$H(D)=-(\frac{9}{15}log\frac{9}{15}+(\frac{6}{15}log\frac{6}{15})$

然后计算单个特征的信息熵，例如年龄的信息熵为：
$$H(D|A_1)=-\frac{5}{15}\ast (\frac{2}{5}log\frac{2}{5}+\frac{3}{5}log\frac{3}{5})-\frac{5}{15}\ast (\frac{3}{5}log\frac{3}{5}+\frac{2}{5}log\frac{2}{5})-\frac{5}{15}\ast (\frac{4}{5}log\frac{4}{5}+\frac{1}{5}log\frac{1}{5})$$
其他特征的信息熵同理，然后可以计算各个特征的信息增益$g(D|A_1)=H(D)-H(D|A_1)$，然后选取信息增益最大的特征作为最优特征。然后基于该特征进行切分，如果分类数据切分出来之后的数据属于同一类则不需要继续切分。

Gini指数

基尼指数的定义为：
$$Gini(p)=\sum _{k=1}^K{p}_k(1-p_k)=1-\sum _{k=1}^K{p}_k^2$$
其中${\sum }_{k=1}^K{p}_k=1$，$p_k$是指样本点属于第$k$类的概率。

在CART决策树中，采用Gini指数来寻找最佳特征，计算每个特征的Gini指数，选择Gini指数最小的作为最有特征，每个特征中Gini指数最小的作为最佳分割点。

代码如下：

#读入数据
import pandas as pd
titanic = pd.read_csv("D:/Learning/train.csv")
#提取有效的数据
y = titanic.Survived
x = titanic[['Pclass','Age','Sex']]
print(x.isnull().sum())#查看空缺值
x["Age"] = x["Age"].fillna(int(x["Age"].mean()))#用均值填补空缺值

#导入所需的模块
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction import DictVectorizer
#数据切分
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3,random_state=1234)
#将离散数据使用One-Hot进行转化
dict = DictVectorizer()
x_train = dict.fit_transform(x_train.to_dict(orient="records")) #orient="records"是将数据转化为一行一行的字典形式
x_test = dict.transform(x_test.to_dict(orient="records"))

#引入决策树API
from sklearn.tree import DecisionTreeClassifier
#拟合模型
dt = DecisionTreeClassifier()
dt.fit(x_train,y_train)

#查看模型效果
print(dt.score(x_test,y_test))
y_pre = dt.predict(x_test)
from sklearn.metrics import classification_report
print(classification_report(y_test,y_pre))

#对模型进行调参，一般对数的深度进行调参
param = {"max_depth": [5, 8, 15, 25, 30]}
from sklearn.model_selection import GridSearchCV
gd = GridSearchCV(dt,param_grid=param,cv=10)
gd.fit(x_train,y_train)
print(gd.best_score_)
print(gd.score(x_test,y_test))
y_pre = gd.predict(x_test)
print(classification_report(y_test,y_pre))

决策树的优点是：(1)简单易理解，可以对结果进行可视化（可视化需要引入外部Graphviz进行配置）(2)数据的需求较少，要求较低
缺点：（1）决策容易过拟合 （2）容易受异常值影响

随机森林

随机森林是属于集成学习中的一种方法。集成学习是通过建立几个模型的组合来预测单一的预测问题。它的工作原理是生成多个分类器，然后各自独立地学习和做出预测。然后合成最后的预测结果。

算法流程

随机抽样

随机森林采用的是Bootstrap有放回抽样，每个样本被抽中的概率为$\frac{1}{n}$，不被抽中的概率为$1-\frac{1}{n}$，在有放回抽样中，每次抽样是独立的，所以$n$次抽样中样本不悲抽中的概率为$(1-\frac{1}{n}{)}^n$，当$n$趋近无穷是，样本呢不被抽中的概率为$\frac{1}{e}$。其中这些未被抽中的数据称为包外数据(Out of Bag,OOB).

Bagging 算法

通过进行多次Bootstrap抽样，每次抽样的数据集训练成为一个弱学习器模型，将获得的多个独立的弱学习器模型进行组合来预测结果。当若学习器是决策树的时候，这种Bagging算法就称之为随机森林。

随机森林概要

首先假设数据集地维度为$M\times N$从数据集中有放回地抽出$m$个样本，然后从N个特征中随机抽取$n$个特征。然后生成决策树，将决策树每次的结果记录下来。再通过多次的训练后，对训练好的决策树进行投票，取投票（单颗树分类结果）最多的那个类别作为整个随机森林的分类结果。若是解决回归问题，则将决策树的每个预测结果取均值作为最终的预测结果。

随机森林在回归问题上，预测的结果是多个决策树的平均值，即$\frac{1}{n}{\sum }_i^n{y}_i$，假设他们是服从独立同分布的，且方差为${\sigma }^2$,那么最终的方差为$\frac{{\sigma }^2}{n}$，从这方面可以说明随机森林是可以一定程度上降低预测方差的。

由于随机森林种存在外包数据，所以可以将外包数据作为模型的测试集，测试模型的误差，这个误差也被称之为外包误差。外包误差就是将错分类的数目除以外包数据的总数（外包数据的回归误差除以外包数据的总数）。故在训练过程中可以通过研究外包数据误差的变化来调参。

特征重要性

随机森林在平时的使用中，不仅可以预测结果，还可以用来判断特征的重要性。可以使用置换算法进行计算，从样本中选取某个特征值进行替换，查看替换结果对模型的影响是否敏感从而判断特征的重要性。

变量的重要性计算公式为：
对于分类数据：
$$v=\frac{n_{y^{\ast }}-n_{y^{\ast \ast }}}{n_{OOB}}$$
对于回归数据：
$$v=\frac{{\sum }_{i\in oob}exp(-(\frac{y_i-y_i^{\ast }}{m}{)}^2)-{\sum }_{i\in oob}exp(-(\frac{y_i-y_i^{\ast \ast }}{m}{)}^2)}{n_{OOB}}$$

其中$y^{\ast }$是替换前的数据，$y^{\ast \ast }$是替换后的数据，$y$是真实数据。
最终将计算得到的结果进行取平均，并归一化就可以得出各个的特征的重要程度。

代码如下

#导入随机森林的API
from sklearn.ensemble import RandomForestClassifier

#建立估计器
rf = RandomForestClassifier()

#定义搜索的树的范围和深度的大小
param = {"n_estimators": [120, 200, 300, 500, 800, 1200], "max_depth": [5, 8, 15, 25, 30]}

# 网格搜索和十折交叉验证
gc = GridSearchCV(rf, param_grid=param, cv=10)
gc.fit(x_train, y_train)
print("准确率：", gc.score(x_test, y_test))
print("查看选择的参数模型：", gc.best_params_)
y_pre = gd.predict(x_test)
#模型的F1值
print(classification_report(y_test,y_pre))

决策树的优点是：（1）模型的运行效率高，准确率高
（2）能够对数据量大的数据集进行处理
（3）能够较好地处理高纬度地数据，且不需要进行降维
（4）能够得出特征的重要性（由于数据集特征较少，本次模型不展示特征的重要性）
（5）能够容纳空缺值，由于算法本身的性质，故在缺失数据中也能够获得较好的结果