深度学习 Day 4——利用RNN玩转股票预测

深度学习 Day 4——利用RNN玩转股票预测

一、前言

活动地址：CSDN21天学习挑战赛

• 本文为365天深度学习训练营 中的学习记录博客
• 参考文章地址： 深度学习100例-循环神经网络（RNN）实现股票预测 | 第9天

在上一周，我们跟着k同学啊学习了利用CNN实现天气识别的功能，并且我们也进行了环境的配置以及在这期间问题的解决，如果大家没有看过我上一周的博客的话，可以推荐大家去看一看，支持一下我的创作，非常感谢！

这是我的学习专栏：Python深度学习专栏

我很希望大家能从中学习到很多知识，我也如此，我们一起学习，一起进步。

好啦，废话不多说，现在已经到了学习活动的第二周了，我们要开始新的一周的学习任务了。

本周的学习任务目标是：利用循环神经网络（RNN）实现股票的预测

二、准备工作

1、我的环境

• 电脑系统：Windows 11
• 语言环境：Python 3.8
• 编译器：PyCharm
• 深度学习环境：TensorFlow 2.3.0
• 我的电脑显卡：NVIDIA GeForce RTX 3070

2、设置GPU

和之前一样，如果使用的时CPU就可以忽略这一点，有条件的话最好使用GPU

import tensorflow as tf

gpus = tf.config.list_logical_devices("GPU")
if gpus:
    tf.config.experimental.set_synchronous_execution(gpus[0], True)
    tf.config.set_visible_devices([gpus[0], "GPU"])

3、加载数据

导入matplotlib库读取股票文件内容以及pandas库来处理数据

import matplotlib.pyplot as plt
import pandas as pd

plt.rcParams['font.sans-serif'] = ['SimHei']    # 正常显示中文
plt.rcParams['axes.unicode_minus'] = False  # 正常显示负号

data = pd.read_csv('E:\深度学习\数据\SH600519.csv')
plt.show()

可以发现一共有2426行×8列数据，然后我们可以设置前2126天的数据作为训练集，表格从0开始计数，后300作为测试集。

training_set = data.iloc[0:2426 - 300, 2:3].values
test_set = data.iloc[2426 - 300:, 2:3].values

三、数据预处理

1、归一化

我们需要进行数据归一化的处理，因为这可以使得预处理的数据被限定在一定的范围内，从而消除奇异样本数据导致的不良影响，数据归一化处理后，可以加快梯度下降求最优解的速度，且有可能提高精度。

from sklearn.preprocessing import MinMaxScaler
from sklearn import metrics

sc = MinMaxScaler(feature_range=(0, 1))
training_set = sc.fit_transform(training_set)
test_set = sc.transform(test_set)

2、设置训练集和测试集

可能有人会问我们为什么要设置测试集和训练集，我们先来了解一下深度学习的简单流程：

1. 使用大量和任务相关的数据集来训练模型
2. 通过模型在数据集上的误差不断迭代训练模型，得到对数据集拟合合理的模型
3. 将训练好调整好的模型应用到真实的场景中

我们的最终目的就是将训练好的模型运用到真实的环境中去，而我们希望模型在真实的数据上预测的结果误差越小越好，在真实环境中的误差被称作泛化误差，但是我们不能通过直接将繁华误差当作了解模型泛化能力的信号，那是因为在运用环境以及训练模型之间往复代价很高，同时也不能之间使用训练模型时的泛化误差来作为真实环境下的泛化误差。

最好的解决方式就是将我们的数据分成两个部分，测试集和训练集。有了测试集，我们想要验证模型的最终效果，只需将训练好的模型在测试集上计算误差，即可认为此误差即为泛化误差的近似，我们只需让我们训练好的模型在测试集上的误差最小即可。

一般来说将数据集的80%作为训练集，20%作为测试集，并且开始构建模型之前就需要对数据集进行划分，还需要对数据进行预处理。

import numpy as np

# 训练集
x_train = []
y_train = []

# 测试集
x_test = []
y_test = []

for i in range(60 , len(training_set)):
    x_train.append(training_set[i - 60:i, 0])
    y_train.append(training_set[i, 0])

for i in range(60 , len(test_set)):
    x_test.append(test_set[i - 60:i, 0])
    y_test.append(test_set[i, 0])

# 对训练集进行打乱
np.random.seed(7)
np.random.shuffle(x_train)
np.random.seed(7)
np.random.shuffle(y_train)
tf.random.set_seed(7)

我们将训练数据转换成数组形式：

x_train, y_train = np.array(x_train), np.array(y_train) # x_train形状为：(2066, 60, 1)
x_test, y_test = np.array(x_test), np.array(y_test)

"""
输入要求：[送入样本数， 循环核时间展开步数， 每个时间步输入特征个数]
"""
x_train = np.reshape(x_train, (x_train.shape[0], 60, 1))
x_test = np.reshape(x_test,  (x_test.shape[0], 60, 1))

四、构建模型

数据处理好之后，就可以开始构建我们的模型了

from tensorflow.keras.layers import Dropout, Dense, SimpleRNN

model = tf.keras.Sequential([
    SimpleRNN(100, return_sequences=True), 
    Dropout(0.1),                         
    SimpleRNN(100),
    Dropout(0.1),
    Dense(1)
])

五、激活模型

# 该应用只观测loss数值，不观测准确率，所以删去metrics选项，一会在每个epoch迭代显示时只显示loss值
model.compile(optimizer=tf.keras.optimizers.Adam(0.001),
              loss='mean_squared_error')  # 损失函数用均方误差

我们只需要记录loss值不需要记录准确率，待会会利用这些loss绘制直观图。

六、训练模型

history = model.fit(x_train, y_train,
                    batch_size=64,
                    epochs=20,
                    validation_data=(x_test, y_test),
                    validation_freq=1)                  #测试的epoch间隔数

model.summary()

运行出来的结果是：

Epoch 1/20
33/33 [==============================] - 1s 27ms/step - loss: 0.1262 - val_loss: 0.0670
Epoch 2/20
33/33 [==============================] - 1s 20ms/step - loss: 0.0172 - val_loss: 0.0786
Epoch 3/20
33/33 [==============================] - 1s 20ms/step - loss: 0.0126 - val_loss: 0.0037
Epoch 4/20
33/33 [==============================] - 1s 20ms/step - loss: 0.0089 - val_loss: 0.0160
Epoch 5/20
33/33 [==============================] - 1s 20ms/step - loss: 0.0064 - val_loss: 0.0352
Epoch 6/20
33/33 [==============================] - 1s 20ms/step - loss: 0.0052 - val_loss: 0.0207
Epoch 7/20
33/33 [==============================] - 1s 19ms/step - loss: 0.0048 - val_loss: 0.0307
Epoch 8/20
33/33 [==============================] - 1s 20ms/step - loss: 0.0046 - val_loss: 0.0255
Epoch 9/20
33/33 [==============================] - 1s 19ms/step - loss: 0.0037 - val_loss: 0.0246
Epoch 10/20
33/33 [==============================] - 1s 20ms/step - loss: 0.0031 - val_loss: 0.0069
Epoch 11/20
33/33 [==============================] - 1s 20ms/step - loss: 0.0029 - val_loss: 0.0077
Epoch 12/20
33/33 [==============================] - 1s 20ms/step - loss: 0.0027 - val_loss: 0.0097
Epoch 13/20
33/33 [==============================] - 1s 20ms/step - loss: 0.0023 - val_loss: 0.0091
Epoch 14/20
33/33 [==============================] - 1s 19ms/step - loss: 0.0024 - val_loss: 0.0084
Epoch 15/20
33/33 [==============================] - 1s 20ms/step - loss: 0.0020 - val_loss: 0.0092
Epoch 16/20
33/33 [==============================] - 1s 19ms/step - loss: 0.0019 - val_loss: 0.0084
Epoch 17/20
33/33 [==============================] - 1s 20ms/step - loss: 0.0020 - val_loss: 0.0057
Epoch 18/20
33/33 [==============================] - 1s 19ms/step - loss: 0.0018 - val_loss: 0.0064
Epoch 19/20
33/33 [==============================] - 1s 20ms/step - loss: 0.0018 - val_loss: 0.0071
Epoch 20/20
33/33 [==============================] - 1s 19ms/step - loss: 0.0016 - val_loss: 0.0056
Model: "sequential"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
simple_rnn (SimpleRNN)       (None, 60, 100)           10200     
_________________________________________________________________
dropout (Dropout)            (None, 60, 100)           0         
_________________________________________________________________
simple_rnn_1 (SimpleRNN)     (None, 100)               20100     
_________________________________________________________________
dropout_1 (Dropout)          (None, 100)               0         
_________________________________________________________________
dense (Dense)                (None, 1)                 101       
=================================================================
Total params: 30,401
Trainable params: 30,401
Non-trainable params: 0
_________________________________________________________________

七、可视化结果

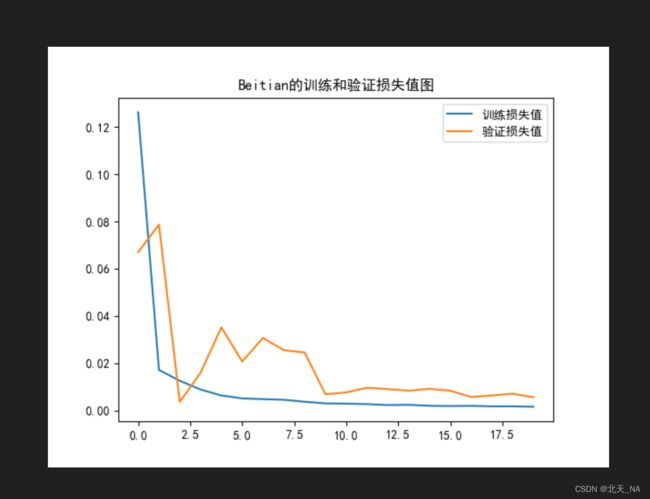
通过matplotlib将我们训练出来的loss值进行直观的绘图：

plt.plot(history.history['loss'], label='Training Loss')
plt.plot(history.history['val_loss'], label='Validation Loss')
plt.title('Training and Validation Loss by Beitian')
plt.legend()
plt.show()

运行出来的图片结果为：

可以发现跟原作者的图差不多。

接下来，我们要进行对数据的预测，这是很重要的工作，因为我们就是构建模型之后要对股票后续数据的预测。

将真实数据和我们的预测数据进行对比就可以看出误差大概多少，是不是会偏差很多。

predicted_stock_price = model.predict(x_test)                       
# 测试集输入模型进行预测
predicted_stock_price = sc.inverse_transform(predicted_stock_price) 
# 对预测数据还原---从（0，1）反归一化到原始范围
real_stock_price = sc.inverse_transform(test_set[60:])              
# 对真实数据还原---从（0，1）反归一化到原始范围

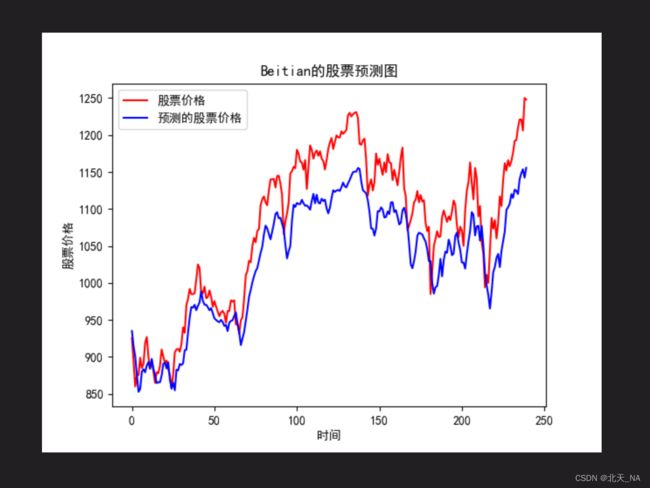
# 画出真实数据和预测数据的对比曲线
plt.plot(real_stock_price, color='red', label='Stock Price')
plt.plot(predicted_stock_price, color='blue', label='Predicted Stock Price')
plt.title('Stock Price Prediction by Beitian')
plt.xlabel('Time')
plt.ylabel('Stock Price')
plt.legend()
plt.show()

预测出来的图为：

可以看出走向基本一致，接下来我们还需要进行更加细致的评估计算工作，来进一步确定我们的模型误差结果。

模型的评估工作需要用到几个数学量，它们分别是：均方误差，均方根误差，平均绝对误差以及决定系数。

数学量	说明
均方误差	预测值减真实值求平方后求均值
均方根误差	对均方误差开方
平均绝对误差	预测值减真实值求绝对值后求均值
决定系数	反映模型拟合优度的重要的统计量

好啦，我们现在开始进行评估工作：

MSE = metrics.mean_squared_error(predicted_stock_price, real_stock_price)
RMSE = metrics.mean_squared_error(predicted_stock_price, real_stock_price)**0.5
MAE = metrics.mean_absolute_error(predicted_stock_price, real_stock_price)
R2 = metrics.r2_score(predicted_stock_price, real_stock_price)

print('均方误差: %.5f' % MSE)
print('均方根误差: %.5f' % RMSE)
print('平均绝对误差: %.5f' % MAE)
print('R2: %.5f' % R2)

最后的评估结果是：

均方误差: 2832.55128
均方根误差: 53.22172
平均绝对误差: 46.33842
R2: 0.59098

其中，均方误差、均方根误差以及平均绝对误差都是值越小越好，而系数R2则是越大表示模型越好，后续的博客我也会专门来讲一下这四者的含义以及计算公式。

到这里整个过程也就结束啦。

八、最后我想说

经过两天的学习终于把第二周的博客写完了，期间也遇见了一些问题让我花费啦很多的时间，后续的博客我就会来说一下我遇见的问题，以及我是如何解决的，请大家继续关注我接下来的博客，非常感谢！

这一周我们学习的是RNN和上一周的CNN有所区别，但是都是深度学习的范畴内。

本次的博主提供的案例我觉得非常有实际作用，以后我们也可以多写一些有助于简化我们生活的代码哈哈哈。

总的来说难确实很难，所以仍要继续努力才行，生活可不会因此就施予好运，所以的好运都要来自自己的努力奋斗，努力的人总不会太差。

最后，谢谢大家的阅读，也期待着大家的点赞收藏转发三连，你们的鼓励将是我创作的最大动力，我也会持续的更新我的CSDN博客的，以后也会更新其他的学习内容。