强化学习笔记_6_价值学习高级技巧

1. Experience Relay 经验回放

1.1. shortcomings of original algorithms

• Waste of Experience

  transition $(s_t,a_t,r_t,s_{t+1})$，称从开始到结束所有的transition为经验，原始算法中每次使用一个transition后丢弃。

• Correlated Updates

  原始算法中，相邻transition具有相关性，实验证明这种相关性不利于训练。

1.2. Experience Relay

• replay buffer：可储存最新的n个transition，n为超参数，通常设置在$10^5-10^6$之间。

• TD with Experience Relay

  • 目标函数：$L(w)=\frac{1}{T}{\sum }_{t=1}^T\frac{{\delta }_t^2}{2}$

  • Stochastic gradient descent (SGD)

    每次从replay buffer中随机均匀抽取一个transition $(s_1,a_i,r_i,s_{i+1})$；

    计算TD error ${\delta }_i$；

    随机梯度：$g_i=\frac{\partial {\delta }_i^2/2}{\partial w}={\delta }_i\cdot \frac{\partial Q(S_i{a}_i;w)}{\partial w}$；

    SDG：$w\leftarrow w-\alpha \cdot g_i$。

  • 实际中常常随机抽取多个transition（一个batch），计算多个随机梯度，以平均值更新参数$w$。

  • 打破了序列的相关性，可重复利用过去的经验。

1.3. Prioritized Experience Relay 优先经验回放

• Basic Idea

  不是所有transition都有相同的重要性。可以用TD error的值判断重要性，绝对值越大，说明网络越不熟悉该场景，其重要性越大。

• Importance Sampling

  使用非均匀抽样代替均匀抽样：

  • Option 1：抽样概率 $p_t\propto |{\delta }_t|+ϵ$（$ϵ$避免概率为0）

  • Option 2：抽样概率$p_t\propto \frac{1}{rank(t)}$

    $rank(t)$为${\delta }_t$的序号，${\delta }_t$绝对值越大，序号就越小，抽样概率越大。

• Scaling Learning Rate

  • 非均匀抽样，不同transiton得到的概率不同，会导致DQN的预测有偏差，应相应调整学习率以抵消偏差。

  • SGD：$w\leftarrow w-\alpha \cdot w$

  • 将学习率$\alpha$乘以$(n\cdot p_t{)}^{-\beta }$，超参数$\beta \in (0,1)$，起初较小，逐渐增大到1

    对于均匀抽样，$p_1=p_2\cdot \cdot \cdot =p_n=\frac{1}{n},n{\cdot }_t=1$；

    对于非均匀抽样，$p_t$越大，学习率越小。

• Update TD Error

  • 为每一条transition计算TD error ${\delta }_t$
  • 对新收集到还未使用的transition，${\delta }_t$未知，将其赋最大值，即拥有最高的优先级
  • 训练DQN的同时更新${\delta }_t$，权重也随之

2.Target Network ＆ Double DQN

2.1. Bootstrapping 自举

在强化学习中，指用一个估算去更新同类的估算：“using an estimated value in the update step for the same knid of estimated value.”

TD算法中，使用一个transition更新参数$w$。TD target中使用到了$s_{t+1}$，说明为了更新DQN在$t$时刻的估计，需使用到DQN在$t+1$时刻的预测。

2.2. Problem of Overestimation

• TD算法导致DQN高估行动价值action-value，原因：

  • Maximization：计算TD target时使用了最大化计算${\max }_{a}Q(s_{t+1},a;w)$，导致高估

    

    

  • Bootstrapping：用自己的估计更新自己，高估会一步步叠加（正反馈）

    计算TD target时使用到了$q_{t+1}={\max }_{a}Q(s_{t+1},a;w)$，并使用其更新$Q(s_t,a_t;w)$。

    如果DQN高估行动价值，则$Q(s_{t+1},a_t;w)$是高估的，maximization导致其进一步高估。

    更新参数，导致被更新参数高估$Q(s_t,a_t;w)$。

• Why is overestimation a shortcoming?

  均匀高估不会影响决策，不均匀高估影响决策。由于每个二元组$(s_t,a_t)$在replay buffer中的概率不同，故高估的程度不同。

• Solution：target network（解决bootstrapping），double DQN（解决maximization）

2.3. target network

target network: $Q(s,a;w^{-})$，与DQN网络$Q(s,a;w)$结构相同，参数不同。

使用$Q(s,a;w)$控制agent并收集经验transitions；

使用$Q(s,a;w^{-})$计算TD target，$y_t=r_t+\gamma \cdot {\max }_{a}Q(s_{t+1},a;w^{-})$。

• 使用一个transition对$w$进行参数更新的过程：
  • 观测得到transition $s_t,a_t,r_t,s_{t+1}$
  • TD target: $y_t=r_t+\gamma \cdot {\max }_{a}Q(s_{t+1},a;w^{-})$
  • TD error: ${\delta }_t=Q(s_t,a_t;w)-y_t$
  • SGD: $w\leftarrow w-\alpha \cdot {\delta }_t\cdot \frac{\partial Q(s_t,a_t;w)}{\partial w}$
• Periodically update $w^{-}$
  • Option1: $w^{-}\leftarrow w$
  • Option2: $w^{-}\leftarrow \tau \cdot w+(1-\tau \cdot w^{-})$

由于使用了另一个网络计算TD error，使用target network可以一定程度减小bootstrapping导致DQN高估的程度，但依然无法解决maximization导致的高估。同时，由于target network的参数依赖于DQN网络，故bootstrapping依然存在。

2.4. double DQN

• 计算TD target的方法：

  DQN：
  $$\begin{array}{rl}{a}^{\ast }& =\arg \underset{a}{\max }Q(s_{t+1},a;w)\\ y_t& =r_t+\gamma \cdot Q(s_{t+1},a^{\ast };w)\end{array}$$
  target network:
  $$\begin{array}{rl}{a}^{\ast }& =\arg \underset{a}{\max }Q(s_{t+1},a;w^{-})\\ y_t& =r_t+\gamma \cdot Q(s_{t+1},a^{\ast };w^{-})\end{array}$$
  double DQN:
  $$\begin{array}{rl}{a}^{\ast }& =\arg \underset{a}{\max }Q(s_{t+1},a;w)\\ y_t& =r_t+\gamma \cdot Q(s_{t+1},a^{\ast };w^{-})\end{array}$$
  

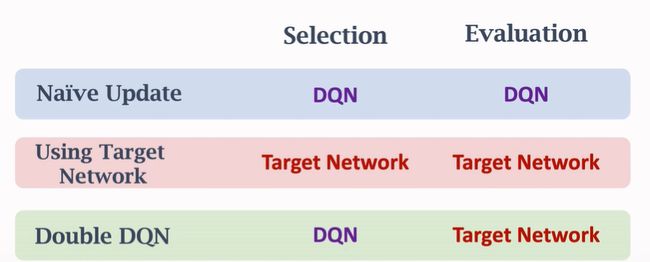
  大幅提升性能，虽然不能彻底消除高估，但是高估不太严重。

• Why does double DQN work better?

  Selection using DQN: $a^{\ast }=\arg {\max }_{a}Q(s_{t+1},a;w)$

  Evaluation using target network: $y_t=r_t+\gamma \cdot Q(s_{t+1},a^{\ast };w^{-})$
  $$Q(s_{t+1},a^{\ast };w^{-})\le \underset{a}{\max }Q(s_{t+1},a;w^{-})$$
  上式左侧Double DQN选择的$a^{\ast }$实际上不是$Q$值最大的动作，以部分避免高估。

3.Dueling Network

3.1. Advantage Function

• Definations

  Optimal action-value function: $Q^{\ast }(s,a)={\max }_{\pi }{Q}_{\pi }(s,a)$

  Optimal state-value function: $V^{\ast }(s)={\max }_{\pi }{V}_{\pi }(s)$

  Optimal advantage function（优势函数）: $A^{\ast }(s,a)=Q^{\ast }(s,a)-V^{\ast }(s)$

• Properties of Advantage Function

  Theorem 1: $V^{\ast }(s)={\max }_a{Q}^{\ast }(s,a)$
  $$\begin{array}{rl}{A}^{\ast }(s,a)& =Q^{\ast }(s,a)-V^{\ast }(s)\\ \underset{a}{\max }{A}^{\ast }(s,a)& =\underset{a}{\max }{Q}^{\ast }(s,a)-V^{\ast }(s)=0\end{array}$$
  将进行如下变换：
  $$\begin{array}{rl}{A}^{\ast }(s,a)& =Q^{\ast }(s,a)-V^{\ast }(s)\\ Q^{\ast }(s,a)& =V^{\ast }(s)+A^{\ast }(s,a)-ma{x}_a{A}^{\ast }(s,a)\end{array}$$
  Theorem 2: $Q^{\ast }(s,a)=V^{\ast }(s)+A^{\ast }(s,a)-ma{x}_a{A}^{\ast }(s,a)$

3.2. Dueling Network

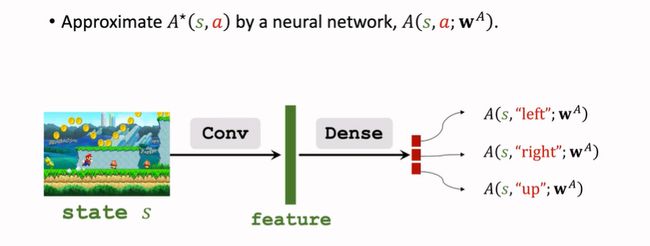
• Approximation Advantage Function $A(s,a;w^A)$

  

• Approximation State-Value Function $V(s;w^V)$

  

• Dueling Network

  根据Theorem 2，得到对动作价值函数的近似（与DQN相同）：
  $$Q^{\ast }(s,a;w^A,w^V)=V^{\ast }(s;w^V)+A^{\ast }(s,a;w^A)-ma{x}_a{A}^{\ast }(s,a;w^A)$$
  [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-xe0bBddO-1672473344043)(null)]

  Dueling Network与DQN的输入输出均相同，但是网络结构不同。

• Training

  学习参数$w=(w^A,w^V)$，训练过程与DQN相同，也可以应用其他高级技巧。

3.3. Overcome Non-identifiability

• Problem of Non-identifiability

  Equation 1: $Q^{\ast }(s,a)=V^{\ast }(s)+A^{\ast }(s,a)$

  Equation 2: $Q^{\ast }(s,a)=V^{\ast }(s)+A^{\ast }(s,a)-ma{x}_a{A}^{\ast }(s,a)$

  Equation 1中，无法通过学习$Q^{\ast }$唯一确定$V^{\ast },A^{\ast }$，如果$A^{\ast }$增加10，$V^{\ast }$减小10，得到的输出$Q^{\ast }$不变。若$A,V$两个网络存在反向的波动，二者相加后的输出呈现稳定，但是实际上$A,V$两个网络训练效果都不好。

  Equation 2解决了不唯一性，如果$A^{\ast }$增加10，$V^{\ast }$减小10，得到的结果减小10。