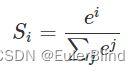深度学习是怎么工作的
深度学习是什么
要解解释深度学习是什么,我们不妨先看看深度学习解决的都是什么样的问题。
深度学习解决什么问题
-
按照信号角度划分
领域 应用 文本领域(NLP) 填词
问答
生成诗歌
词法、语法分析,错误修正
文本分类、文本摘要
情感分析、代码生成、代码解析图像领域 OCR
图片分类
目标检测
目标分割 (同类目标分割、实例目标分割)
图像生成(人脸图像生成、动漫图像生成、风格迁移)音频领域 语音降噪
声音克隆
声纹识别
语音转文字多模态 根据文本生成图像
描述图像景象其他 趋势预测
故障诊断 -
按照任务类型分类:
显然,根据其处理信号的领域来看,我们的直观感觉都放在了一个宏观问题的角度,这很难让我们看清深度学习任务的本质。所以我们按照深度学习任务类型来分区分,就会有一个更直观的概念。
-
回归任务
回归任务最明显的特征是其输出是连续值,常用于对一些趋势的预测,如天气趋势、购买量、点击量、股票趋势等。
-
分类任务
分类任务的输出是离散值,其输出状态一般个数是有限的,最常见的图像分类、目标检测等都属于该类任务
为什么说按照其任务类型来区分,我们就能直观的理解深度学习呢?原因在于,按照处理任务的角度来区分后,我们能够更直观的看到任务的输入与输出。不管是回归任务,还是分类任务,其输入的都是所谓的数据,是什么样的数据呢?这个取决于解决的问题,如图像处理,其数据就是每一张图片;文本任务中,数据就是给定的文本。这么说还不够好理解,有两个更专业的词汇描述得更贴切,一个叫特征,结合OOP的思想,这里的特征其实指的就是属性,如西瓜的颜色、重量、体积等,都是西瓜的一个特征。另一个词叫做张量,张量可以理解为多个对象的特征集合,深度学习的输入数据就是张量。
深度学习如何工作
在之前的描述中,我们能够理解对于一个深度学习函数的输入与输出了,但是跟我们平时写代码一样,对于一个确定的输入,以及一个确定的输出,我们的实现可以有很多种,那么深度学习是如何来统一这种形式的呢?这里的统一形式有两层含义,一个是指给定输入、输出的情况下,深度学习用一种统一的方法处理,使其能够正确输入输出;另一层含义是指,对于分类任务和回归任务两种不同类型任务,在深度学习中,其处理方案也是一致的。
从一个函数拟合的例子讲起(线性回归)
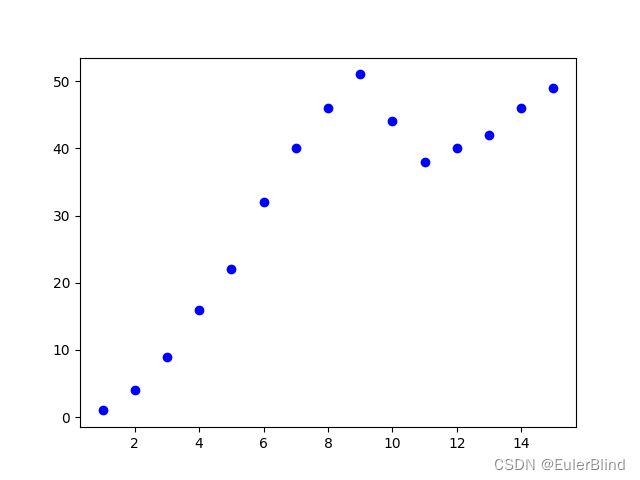
假如现在有一堆二维数据,
x = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]
y = [1, 4, 9, 16, 22, 32, 40, 46, 51, 44, 38, 40, 42, 46, 49]
这些数据在二维平面上展示出来如下图所示
现在的需求是,我们需要找到一条直线,使图中每个点到直线的距离和最短。显然,这个会涉及到直线方程,不妨假设,该直线方程为y=ax+b,其中a,b是参数。这个问题就可以转换为我们要求解一个合适的a,b使图中每个点到直线的距离和最短。那么使用深度学习的方案会如何处理呢?首先会随便找个a、b,然后跟图中的点依次计算距离差求和(我们记做损失loss)。现在假设选定a=0.5,b=0.5,loss =-412.5, 那么在图像上展示出来如下图所示,红色线代表当前的预测函数
之后的操作,如下代码所示,首先关注函数fit_grad_desc,在该函数内,主要流程如下:
1、首先随机取值a、b
2、进入循环,目的是更新参数a、b。更新的方法在grad_desc中,后面会讲。
3、计算当前参数下的损失(此处完全是为了可视化损失变化的过程)
4、绘制图像,使其可视化
然后我们关注一下grad_desc函数,之前也说了,该函数的作用主要就是为了更新参数a,b。那么如何更新a,b呢?
其实本质上就干了两件事,首先计算当前数据下,a、b的梯度(偏导数),然后沿逆梯度方向更新参数a、b。
x = np.array([1, 2, 3, 4, 5, 6, 7, 8])
y = np.array([1, 4, 9, 16, 22, 32, 34, 35])
def grad_desc(a, b, points, lr):
a_gradient = 0
b_gradient = 0
N = float(len(points))
for i in range(0, len(points)):
x = points[i, 0]
y = points[i, 1]
y_hat = a * x + b
point_loss = (y_hat - y)
a_gradient += x * point_loss
b_gradient += point_loss
grad_a = 2 / N * a_gradient
grad_b = 2 / N * b_gradient
new_a = a - (lr * grad_a)
new_b = b - (lr * grad_b)
return new_a, new_b
def fit_grad_desc(lr=0.01):
a = np.random.randn()
b = np.random.randn()
line_x = np.arange(0, 15, 0.1)
for i in range(30):
a, b = grad_desc(a, b, points, lr)
y_pred = a * x + b
line_y = a * line_x + b
loss = (y_pred - y).sum()
print("loss:", loss, 'a:', a, 'b:', b)
pyplot.scatter(x, y, c='b', marker='o')
pyplot.plot(line_x, line_y, c='r', label='grad_desc')
pyplot.plot(line_x, line_y1, c='b', label='scipy_fit')
pyplot.show()
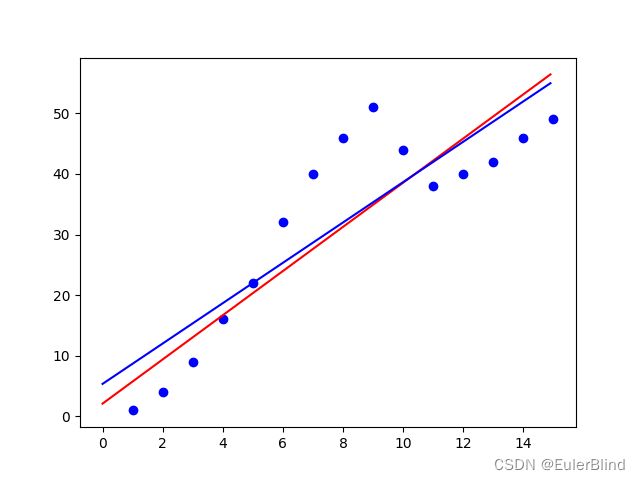
在使用学习率lr=0.01,迭代30次以后,我们能得到的效果如何呢?如下图所示(红色线是梯度下降拟合,蓝色线是使用scipy拟合),此时
a =3.644290748106896,b= 2.1175316102868713,loss =-10.922136072869428,显然,此时的效果比刚开始的拟合效果会更好。
如果能理解上述过程,那么恭喜你,你已经理解了深度学习的本质了。通俗来讲,深度学习本质上,对给定数据的一种拟合。当然,换一个角度,也是对已有数据的一种压缩,或者说是对数据中蕴含知识的压缩。
另外此处要说明的是,我们在这个过程中,所求的梯度,不是原始数据的梯度,具体来讲,我们对于原始数据(向量)x、y本身都是能够使用方法np.gradient()方法求解其梯度,而我们所需要的梯度是对于求解参数a,b的梯度,当然,在一些框架内部,已经封装过,此处提出知识为了方便大家能够更好理解梯度下降的过程。同样的,我们可以用另外的语言来描述一下梯度下降,梯度下降是一种用于在一个高维参数平面寻找最优参数的一种方法。
线性与非线形问题
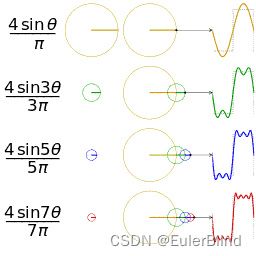
通过上面线形回归的例子,我们大体上能够理解深度学习训练的过程,但还不够好,因为有个很重要的问题没有被解决,那就是非线的问题。拟合的过程中,由于我们给定的模型是线形模型,从而就算是最优解,也不能足够好的拟合给定数据,如何更好的拟合给定数据呢?答案就是引入非线形函数。但随之而来的问题是,非线形函数那么多,该引入什么样的非线形函数?这个问题我们可以从 傅立叶变换 中获得一些启发。我们知道,对于任何复杂的波纹,都能够通过频域转换,分解为多个三角函数进行叠加拟合(傅立叶变换不知道也没关系,可以参考下图)。
回到开始的问题,我们需要什么样的非线形函数?
1、函数本身需要满足非线形特质,分段、二次、三次、对数、指数都能满足。
2、计算需要足够简单,至少需要对计算机而言,要足够简单,因为随着我们数据增多,网络(模型)规模扩大,只有足够简单的函数才能更快的被计算。
3、需要对模型友好(这个稍微深入一点就能了解到关于梯度消失以及梯度爆炸的问题,这个本期不深入讨论)‘
深度学习中,通常在神经元最终输出前加上非线形函数。我们可以使用如下模型来演示加入非线形后的效果
class MyModel1(nn.Module):
def __init__(self):
super(MyModel1, self).__init__()
self.fc1 = nn.Linear(1, 1)
self.sf1 = nn.Parameter(torch.rand(1)[0])
self.fc2 = nn.Linear(1, 1)
self.sf2 = nn.Parameter(torch.rand(1)[0])
self.fc3 = nn.Linear(1, 1)
self.sf3 = nn.Parameter(torch.rand(1)[0])
self.fc4 = nn.Linear(1, 1)
self.sf4 = nn.Parameter(torch.rand(1)[0])
def forward(self, x):
x = self.sf1 * torch.sigmoid(self.fc1(x)) + \
self.sf2 * torch.tanh(self.fc2(x)) + \
self.sf3 * torch.tanh(self.fc3(x)) + \
self.sf4 * torch.tanh(self.fc4(x))
return x
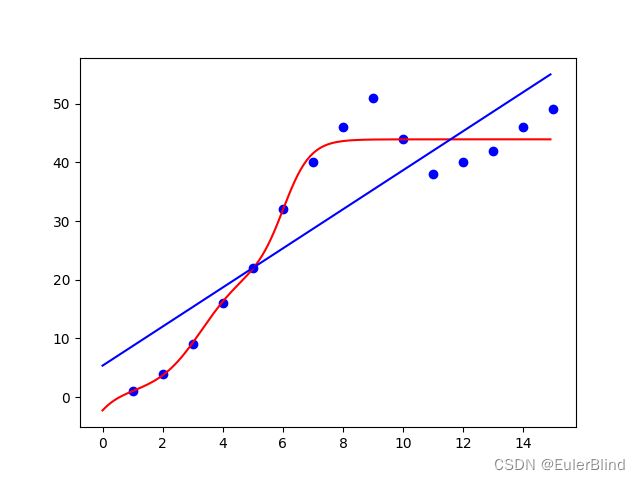
其拟合效果如下图所示,可以发现的是,相比于单一的线性模型,该模型的拟合效果更好(值得一提的是,在机器学习中,并不是拟合效果越好,模型的实际效果就越好,即过拟合问题,这里暂不深究)。
回归问题于分类问题统一形式
之前我们有说到,深度学习中,对于回归问题和分类问题都是以相同的形式在处理,这里相同的形式指的是核心逻辑,或者叫核心方案是一致的,都是使用梯度下降(有很多变种,暂不细究)的方式来处理,也即是前文所述的所有流程。那两者区别又体现在哪里呢?两者的区别主要体现在对于输出的处理。
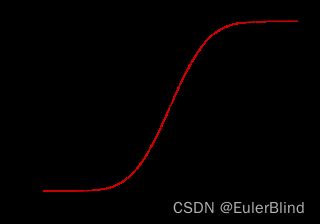
对于回归问题,在输出的时候,通常使用sigmoid一类激活函数,至于sigmoid长什么样子(前文有用过,没有细讲),如下图所示,首先可以看出该函数是一个连续函数,当函数作用在该函数上后,是可以产生连续输出结果的。
对与分类问题,其输出函数通常会加上softmax函数,这里有必要说明一下softmax函数。softmax函数可以将前面输出的多个结果化归到其中一个类别。其公式如下:
光看公式体会没那么直观,举个例子,对于一个猫狗图片分类任务,假如现在前置的网络输出输出猫的得分50,狗的得分120(这里这个得分取决于分类网络的输出),经过softmax后,首先会计算是猫的概率(50/(50+120))=0.29,狗的概率(120/(50+120))=0.71,显然是狗的概率大于是猫的概率,从而判定当前图片是狗。为什么需要softmax,直接比较数值大小不也能出来结果么?1、往往前置网络输出的数值范围是不确定的,意味着只能遍历求解。2、前置网络输出的类别个数对于某个网络(模型)而言可以确定,但是不同网络下是无法确定的,没有一种统一处理方式。总之,softmax函数会让组内形成竞争关系,从而更容易输出类别最大值。
深度学习工程步骤概览
-
数据准备
- 数据采集
- 数据清洗
- 数据标注
-
模型训练
- 模型结构构建
- 网络训练
- 网络调优(超参数调整)
- 网络及权重保存
-
算法部署
- 将上一步的网络结构以及权重选用合适的硬件设备部署
- 服务形式部署
- 移动端部署
- 专用硬件部署(TPU等)
代码附件
import torch
import torch.nn as nn
import numpy as np
from matplotlib import pyplot as plt
import scipy.stats as st
x = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15])
y = np.array([1, 4, 9, 16, 22, 32, 40, 46, 51, 44, 38, 40, 42, 46, 49])
data_x = torch.from_numpy(x).float()
data_y = torch.from_numpy(y).float()
slope, intercept, r_value, p_value, std_err = st.linregress(x, y)
print('slope:', slope, 'intercept:', intercept, )
line_x = np.arange(0, 15, 0.1)
line_st = slope * line_x + intercept
# model
class MyModel(nn.Module):
def __init__(self):
super(MyModel, self).__init__()
self.linear = torch.nn.Linear(1, 1)
def forward(self, x):
y_pred = self.linear(x)
return y_pred
class MyModel1(nn.Module):
def __init__(self):
super(MyModel1, self).__init__()
self.fc1 = nn.Linear(1, 1)
self.sf1 = nn.Parameter(torch.rand(1)[0])
self.fc2 = nn.Linear(1, 1)
self.sf2 = nn.Parameter(torch.rand(1)[0])
self.fc3 = nn.Linear(1, 1)
self.sf3 = nn.Parameter(torch.rand(1)[0])
self.fc4 = nn.Linear(1, 1)
self.sf4 = nn.Parameter(torch.rand(1)[0])
def forward(self, x):
x = self.sf1 * torch.sigmoid(self.fc1(x)) + \
self.sf2 * torch.tanh(self.fc2(x)) + \
self.sf3 * torch.tanh(self.fc3(x)) + \
self.sf4 * torch.tanh(self.fc4(x))
return x
def train(model, lr=0.01, epochs=100):
loss_fn = torch.nn.MSELoss()
opt = torch.optim.Adam(model.parameters(), lr)
for epoch in range(epochs):
x_train = data_x.view(-1, 1)
y_train = data_y.view(-1, 1)
y_pred = model(x_train)
loss = loss_fn(y_pred, y_train)
opt.zero_grad()
loss.backward()
opt.step()
print('epoch:', epoch, 'loss:', loss.item())
# a = model.linear.weight.item()
# b = model.linear.bias.item()
# line_y = a * line_x + b
# with torch.no_grad():
# line_y = model(torch.from_numpy(line_x).float().view(-1, 1)).detach().numpy()
# plt.scatter(x, y, c='b', marker='o')
# plt.plot(line_x, line_y, c='r')
# plt.plot(line_x, line_st, c='b')
# plt.show()
print(list(model.parameters()))
torch.save(model.state_dict(), 'model.pth')
with torch.no_grad():
line_y = model(torch.from_numpy(line_x).float().view(-1, 1)).detach().numpy()
plt.scatter(x, y, c='b', marker='o')
plt.plot(line_x, line_y, c='r')
plt.plot(line_x, line_st, c='b')
plt.show()
if __name__ == '__main__':
train(MyModel(), lr=0.1, epochs=30)
# train(MyModel1(), lr=0.1, epochs=250)