最优传输论文（七）Reliable Weighted Optimal Transport for Unsupervised Domain Adaptation

前言

在开始今天的论文讲解之前，首先提出几个问题：
1.为什么决策边缘的样本容易被错误传输？
边缘样本的特征和多个类别的源域样本的特征接近，很有可能负迁移。即决策边缘的样本与源域样本建立了错误的联系，被分到了错误的类；也就是在耦合矩阵中不应该建立传输的样本间建立了传输。
2.如何找到决策边缘样本？
3.如何衡量样本转移的准确度？

本文主要计算三个值，基于SSR的加权最优传输损失Lg，判别质心损失Lp,以及最传统的源域分类损失Lcls。
1.SSR代价矩阵Q为样本属于类别的概率矩阵，动态平衡依靠样本特征和类别中心距离计算的概率矩阵D和分类器对目标域样本预测的概率矩阵M。
采用巧妙的A distance方法，最初训练阶段因为域间隔远，主要依靠D，到了后期，两个域开始重合无法区分，主要依靠M基于分类器Gy对目标样本的训练，此时Gy也已得到迭代训练性能相对而言不错。
2.将R=（1-Q）与成本矩阵C相乘，得到新的成本矩阵Z，Q(j,y s i)越大，两个样本越可能属于同一类，则1-Q乘以C使得成本矩阵Z越小。
3.判别域对齐的动机是属于同一类的样本应该在特征空间中尽可能靠近,因此，提出无监督域适应的判别质心损失Lp。
Lp第一项为源样本特征与对应类别中心的距离。
第二项用样本i属于类别k的概率Q乘以样本i与类别k的中心的距离，概率高时期望距离小，概率低时期望距离大，这个地方其实我还有点迷糊，总感觉应当是1-Q乘以距离
补充：今天请教李沂洋师哥感觉明白了不少，Eq10的第二项高概率的Q乘以目标域样本和他对应的类的类别中心距离，使得在反向传播过程中式子比重变大，能够得到较大的优化，充分降低样本和类别中心距离，使得类内样本更加紧凑，类间距离更大。（同理，也是因为样本和不相关的类赋予了小权重，反向传播过程中没有太大变化，实现了距离的变大）。
第三项为正则化项，求得两两之间类别中心的距离。

Introduction

Reliable Weighted:可靠的加权，本质上是为样本在特征空间中的距离加权。
大多数基于最优传输的工作忽略了域内部结构，只实现了粗配对匹配。当目标样本分布在聚类边缘附近或远离它们对应的类中心时，很容易被从源域学习到的决策边界错误分类（即在源域上训练的分类器）。
在本文中，我们提出了用于UDA的可靠加权最优传输(RWOT)，包括新的收缩子空间可靠性(SSR)和加权最优传输策略。
1.SSR通过动态利用特征空间原型信息和域内结构动态测量跨域的样本级域差异。
2.设计了基于SSR的加权最优传输策略，实现了精确的成对最优传输过程，减少了目标域决策边界附近样本带来的负迁移。
3.RWOT还配备了判别质心聚类开发策略来学习有判别力的迁移特征信息。


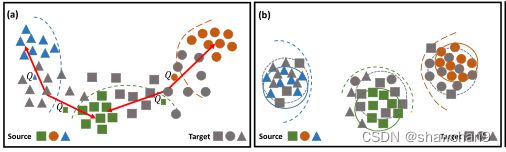
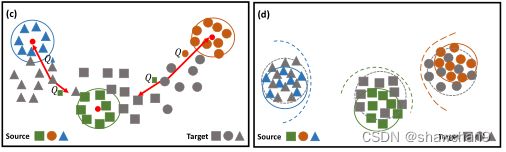
图1.提出的RWOT方法概述。彩色:源样品;灰色:目标样本。彩色虚线:从源域学习的超平面。红点:共享类中心。(a)无监督域适应的一个例子，其中难以对齐的目标样本分布在决策边界附近，导致负迁移。(b)以往方法的分类结果。© RWOT利用空间原型信息D和域内结构M，具有收缩子空间可靠性和判别质心损失的特点。(d)最后一种情况，我们的方案在源和目标域中实现了类内的紧凑性和类间的可分离性。

Reliable Weighted Optimal Transport

传统方法是在概率度量空间中定义一个统计距离，并学习最优传输耦合以最小化该距离。但存在限制：最优传输是粗略的成对匹配。
我们提出了用于无监督域适应的可靠加权最优传输(RWOT)，这是一种端到端训练方法，学习一个特征生成器Gf和一个分类器Gy，如图2所示。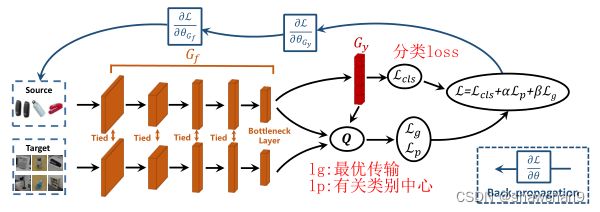

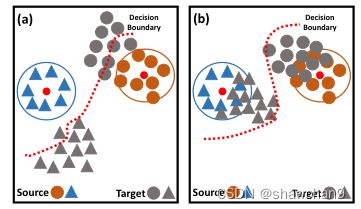
图2。可靠加权最优传输(RWOT)的架构，其中Gf是特征生成器，Gy是自适应分类器;Lg为基于收缩子空间可靠性的加权最优传输损失，Lp为判别质心损失，Lcls为标准交叉熵损失。设计收缩子空间可靠性代价矩阵Q，动态平衡训练过程中空间原型信息和域内结构的贡献:(a)从源域学习到的决策边界对目标样本分类不可靠，源样本被正确地推到对应类的空间原型中。(b)决策边界获得可靠的目标样本域内结构，实现了较好的性能。
注：Q是一个判断目标域样本i属于类别k的概率的矩阵，形状为(n,C)。
Q的估计包括两部分：
1.计算目标域样本的特征和源域类别中心的距离所得概率D。
2.目标域样本的预测类别M。
D和M的形状均为(n,C),平衡两个矩阵，得到Q。

3.1. Shrinking Subspace Reliability

SSR的目标就是判断出较为准确的目标域样本的类别，得到Q(n,C)，C为类别个数，n为目标域样本个数。
考虑到分布在聚类边缘附近的目标样本引起的负迁移，我们提出了收缩子空间可靠性(SSR)来测量跨域的样本级域差异，包括空间原型信息来规范化原型距离，域内结构计算目标样本i属于k类的概率。
为了量化这两个域的空间原型信息，我们定义c s为源域深度特征的类中心，c s∈RC×d，其中C表示Ds(源域)中的类数，每个类别中心用长度为d的向量表示，d为瓶颈层输出神经元的数量。空间原型信息由矩阵D∈Rn×C（n个样本，每个样本属于类别k的概率）定义为:

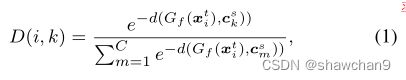
其中d(Gf (xti)，c s k))为目标样本Gf (xti)与第k个源类中心c s k之间的距离，其中k∈{1,2，…C}。N表示训练的批处理大小。与单核方法单调度量两个域差异的方法相比，我们侧重于多核，以全面增强特征表示的可迁移性，实现深度域适应。
注：D(i,k)为目标域样本特征和源域类别中心的距离。距离越近，即d越小，分子越大，D越大，i属于类别k的概率越大。
因此，d(Gf (x t i)， c s k)的多核公式可以定义为:

与特征映射φ相关联的特征核，核K(xs, xt) = <φ(xs)， φ(xt)>，定义为m个PSD核{Ku}的凸组合:

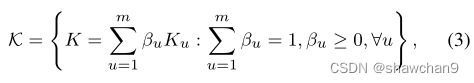
其中K表示多原型核集。对系数{βu}施加了约束，以保证所得到的多核K是特征的，目的：确保更低的测试误差。
为了通过目标样本的伪分类概率来表示域内信息的近似值，我们定义锐化概率注释矩阵M为:

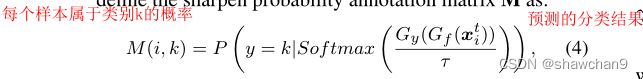
其中M∈Rn×C, M(i, k)表示目标样本i属于标签类k的概率，为预测的分类结果。τ为温度超参数，以获得判别概率，减小域移位。D和M都是衡量i属于k的概率的。
收缩子空间可靠性的目的是定量评估空间原型信息D(i,k)和目标样本域内结构M(i, k)的重要性。SSR的形式由Q定义为:

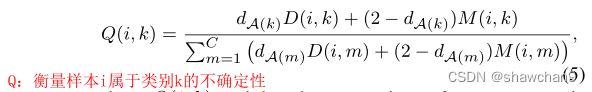
Q衡量样本i属于类别k的不确定性。Q(i, k)对属于k类的目标样本i的不确定性进行加权。 D(i, k)和M(i, k)都测量了目标样本i具有标签k的可能性，D(i, k)是在深度特征空间中测量目标样本i到源域中定义的类中心c s k的距离，M(i, k)由分类器Gy测量，通过分类结果衡量。
我们可以使用A-distance dA来调整权重，衡量两个域之间的散度。A-distance, dA(k)(D s k, D t k) = 2(1−2e(hk))，e(hk)是线性SVM分类器hk区分两个域的误差。
在早期的训练阶段，域间间隔远，可以得到一个接近完美的分类器hk判断出特征属于哪个域，达到e(hk)→0和dA(k)→2。这时Eq 5中分子的第二项消失，网络主要通过第一项进行训练。到了后期，当两个域的分布重合时，分类器hk无法区分两个域，趋向于随机，错误率为50%，因此e(hk) = 0.5, dA(k) = 0。动态过程如图2所示。

3.2. Weighted Optimal Transport

现有的最优传输策略未能充分利用域内结构，导致模糊粗配对匹配产生负迁移。因此，为了减少错误的成对运输过程，我们利用所提出的SSR设计加权最优运输策略。加权最优输运的优化基于加权Kantorovich问题[2]，该问题在Ds和Dt之间寻求一个一般耦合γ∈X (Ds, Dt):

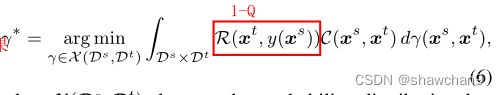
X(Ds, Dt)表示Ds和Dt之间的概率分布。y(xs)是源数据xs的标签，R(xt, y(xs))是根据域内结构基于深度可靠先验知识（通过概率判断出样本类别）的适应矩阵，等于1-Q。若已知两个样本不属于同一个类别，即使特征间距近，也不应当建立传输。
代价函数矩阵C(xs, xt) = ||xs−xt||k表示将概率质量从xs移动到xt的代价，其中k = 2。在我们的最优运输问题中，加权最优运输策略需要估计两个分布之间的自适应传输耦合γ ，并通过最小化γ*的代价来实现特征转换*，找到使传输代价最小的耦合矩阵γ。这是离散的重新表述:

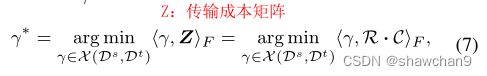
其中γ *∈Rn×n是源域和目标域之间的加权理想耦合矩阵，表示为联合概率测度。Z∈Rn×n为自适应代价函数矩阵。利用深度可靠的先验信息R(x,y)构建更准确的传输成本矩阵。
考虑SSR代价矩阵Q用于评估空间原型信息和目标样本的域内结构，我们首先利用SSR提出了精确的成对最优传输机制。自适应成本矩阵Z的离散式可定义为:

Q越高，则概率越大，进行1-Q乘以成本矩阵C减少传输距离。
(1−Q(j, ysi))的进一步约束有助于解决传统最优运输策略的配对模糊性。通过上述分析，加权最优传输通过减小同类的样本距离，在该特征空间中进行联合优化。可以通过最小化以下目标函数来解决这个问题:

其中F1是分类交叉熵函数。

3.3. Discriminative Centroid Exploitation

判别域对齐的动机是属于同一类的样本应该在特征空间中尽可能靠近。受中心损失的启发，我们提出了无监督域适应的判别质心损失Lp，如下所示:

其中λ是一个超参数，ν是一个约束边界，以控制成对的类间样本之间的距离。
c s ysi作为源域的第y s i类中心，可以通过将多个批量样本的深度特征平均为来近似评估：

其中，如果ysi = k， φ(ysi, k) = 1，否则，φ(ysi, k) = 0。S = (i=1到Nb求和) φ(y s i, k)， k∈{1,2，····，C}为类指标。
理想情况下，类中心的计算应该基于所有的样本，但这个过程非常耗时。在此，我们使用Nb样本计算类中心，其中Nb = mb × n，推荐mb∈{3,4,5}。即Nb一般取3~5个batch的大小。

3.4. Training

在本节中，我们将介绍RWOT的训练过程。我们首先定义源域的标准分类损失来训练分类器，如下所示:

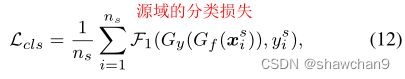
考虑基于收缩子空间可靠性和判别质心损失的加权最优传输，RWOT的总训练目标可以描述为:

其中α， β表示在不同数据集下分别权衡加权最优运输策略和判别域对齐的贡献的超参数。训练过程如算法1所示。