图像处理之常用插值方法：最近邻、双线性、双三次插值

假设现在有:

• 原图像src，大小为MxN，坐标记为(x, y);
• 目标图像dst，大小为PxQ，坐标记为(i, j);

一. 最近邻插值

1. 最近邻插值：
将变换后的图像中的原像素点最邻近像素的灰度值赋给原像素点的方法。（百度百科的解释）

2. 理解：
其实就是根据坐标的变换，找出目标图像中的坐标 对应于 原图像中的坐标，再把原图像中坐标位置的值 填到 目标图像坐标中的值。

3. 转换公式：
根据原图像和目标图像的尺寸，可得：P/M = i/x，Q/N = j/y，所以有：
（1）x = M/P * i，
（2）y = N/Q * j

4. 举例说明
假设原图像大小为3x3，黑色数字1~9表示像素值，红色部分表示坐标，如下图所示：

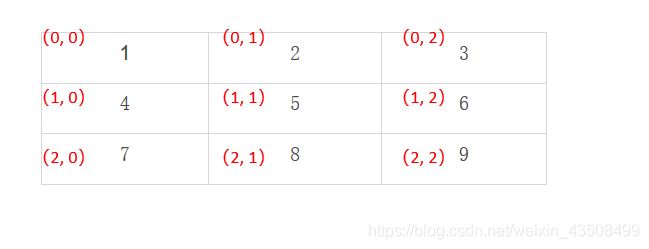
现在要把原图像resize成4x4大小的，则根据上述转换公式，可得如下图所示：（蓝色部分表示目标图像坐标，红色表示原图像坐标）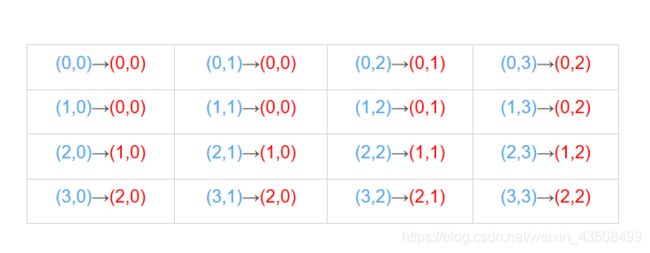

(注意：计算坐标的时候，如果算出来的坐标是小数，通过向下取整转换为整数坐标，例如 0.75→0 )

再根据映射的坐标，把原图像中像素值填到目标图像，最后可得目标图像：

5. 代码

import cv2
import numpy as np

x = np.array([[1, 2, 3],
              [4, 5, 6],
              [7, 8, 9],
              ])
y = cv2.resize(x, (4, 4), interpolation=cv2.INTER_NEAREST)
print(y)

输出结果：

二. 双线性插值

1. 双线性插值
双线性插值，又称为双线性内插。在数学上，双线性插值是有两个变量的插值函数的线性插值扩展，其核心思想是在两个方向分别进行一次线性插值。（来源百度百科）

2. 理解
首先跟最近邻插值一样，先坐标映射，得到目标图像坐标位于原图像的位置，但是这里不再对求出来的小数坐标取整，而是通过举例所求坐标最邻近的四个坐标点，对他们先从X方向作插值，再作Y方向的插值，得到最后的结果，因此也叫 双线性插值。(当然，你要先计算Y方向，再计算X方向也是可以的。)

通过下图进行简单说明，如下图所示：（下面这张图应该讲双线性插值的博客都会用到。）

• 我们求得的映射坐标为P(x,y)；
• Q12, Q22, Q11, Q21是P最近邻的四个点；
• 对Q11, Q21作x方向上的插值，得到R1点的值；
• 对Q12, Q22也作x方向上的插值，得到R2点的值；
• 再对R1, R2作y方向上的插值，就得到P的值。

计算方式，以R1点为例，R1点受到Q11和Q21的影响，

• Q11权重为w1 = ||x - x2|| / || x2 - x1||
• Q21的权重为w2 = || x - x1|| / ||x2 - x1 ||
• 假设Q11, Q21处的像素值为f1和f2， 则计算得到 R1点的值f为：f = w1 * f1 + w2 * f2
• 可以看出规律，离R1越近的点，占的权重也越大。

同理，可得到其他几个点的值。这就是双线性插值的计算过程。
（图像相邻的点坐标相差1，所以上述分母|| x2 - x1||一般等于1 ）

3. 坐标转换公式
（注意，如果用最近邻上面的公式求，得到的结果跟OPENCV计算出来的结果不一样）

（1）x = M/P * (i+0.5) - 0.5，
（2）y = N/Q * (j+0.5) - 0.5

如果计算出来的是负值，就取0，如果超出边界，就取边界值。

4. 举例说明
输入跟之前一样，大小为3x3，像素值为1~9，通过坐标转换，如下图所示：

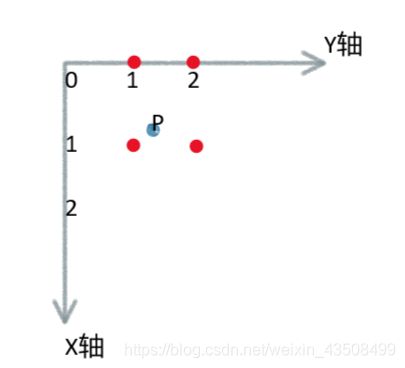
现在目标图像的大小为4x4，根据第2部分的计算方法，我们以目标图像坐标(1, 2)为例，此处求得的映射坐标为P(0.625, 1.375):

• 四个相邻点坐标设为Q12, Q22, Q11, Q21，则他们分别为(0,1), (0,2), (1,1), (1,2)
  

• R1的值为：fr1 = 0.625 x 5 + 0.375 x 6 = 5.375

• R2的值为：fr2 = 0.625 x 2 + 0.375 x 3 = 2.375

• P的值为：fp = 0.625 x 5.375 + 0.375 x 2.375 = 4.25

同理可求得其他位置的值。
（需要注意，这里纵轴方向为x轴，横轴方向为y轴，左上角坐标为圆点）

5. 代码

import cv2
import numpy as np

x = np.array([[1, 2, 3],
              [4, 5, 6],
              [7, 8, 9],
              ], dtype=np.float32)
y = cv2.resize(x, (4, 4), interpolation=cv2.INTER_LINEAR)
print(y)

输出结果为：

三. 双三次插值

（to be continued! 2020.8.11）