聚类算法总结
训练深度学习网络分为监督学习、无监督学习、半监督学习、强化学习。
聚类算法属于无监督学习的范畴,总结的算法有K-Means、Mean Shift、DBSCAN、GMM、凝聚层次聚类、图团体检测。
K-Means(K 均值聚类)
K-Means 是最知名的聚类算法,简单地使用均值。
算法流程:
- 初始化,随机选取k个中心点;
- 遍历所有数据,将每个数据划分到最近的中心点中(欧式距离L2距离);
- 计算每个聚类的平均值,并作为新的中心点;
- 重复2-3,直到这k个中心点不再变化(收敛了),或执行了足够多的迭代,结束。
时间复杂度:O(I * n * k * m)
空间复杂度:O(n * m)
其中n为数据量,I为迭代次数,k为类别数,m为数据点的维数。一般I,k,m均可认为是常量,所以时间和空间复杂度可以简化为O(n),即线性的。
优点:速度快,真正在做的是计算点和组中心之间的距离。
缺点:
- k值需要我们自己来选择,理想情况下,我们希望聚类算法能够帮我们解决分多少类的问题,因为它的目的是从数据中获得一些见解。
- 当数据数量不是足够大时,初始化分组很大程度上决定了聚类,影响聚类结果。
- 使用算术平均值对outlier不鲁棒。可以换成
K-Medians来客服这一点。
K-Means的缺点
K-Medians 是与 K-Means 有关的另一个聚类算法。区别:
- 不是用均值而是用类别的中值向量来重新计算类别中心。这种方法 对异常值不敏感(因为使用中值),但对于较大的数据集要慢得多,因为在计算中值向量时,每次迭代都需要进行排序。
- 步骤2使用的曼哈顿距离L1距离。
K值的选择:参考博客,给出了很多方法,没有完全看懂。????Cross Validation,有人用贝叶斯,还有的用bootstrap。
为什么K-Means使用L2距离??????
而距离度量又是另外一个问题,比较常用的是选用欧式距离。可是这个距离真的具有普适性吗?《模式分类》中指出欧式距离对平移是敏感的,这点严重影响了判定的结果。在此必须选用一个对已知的变换(比如平移、旋转、尺度变换等)不敏感的距离度量。书中提出了采用切空间距离(tangent distance)来替代传统的欧氏距离。
Mean Shift(均值漂移聚类)
均值漂移聚类是基于滑动窗口的算法,它试图找到数据点的密集区域。
算法流程:
- 初始化,从一个以C点(随机选择)为中心,r为半径的滑动窗口(高维球)开始;
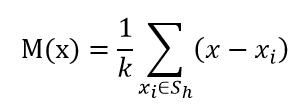
Sh:以x为中心点,半径为h的高维球区域;
k:包含在Sh范围内点的个数;
xi:包含在Sh范围内的点 - 滑动窗口通过将中心点移向窗口内点的均值,来移向更高密度区域;
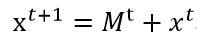
Mt为t状态下求得的偏移均值;
xt为t状态下的中心; - 重复2,直到没有滑动窗口不能容纳更多的点;
- 重复1~3,创建多个滑动窗口,如果存在重叠,保留包含数据点最多的窗口,即为聚类结果,结束。
优点:与 K-means 聚类相比,不需要选择簇数量,因为均值漂移自动发现这一点。
缺点:半径r需要自己选择,对聚类结果影响大。
应用:
- 聚类(K均值聚类)
- 图像分割(将图像映射到特征空间,对采样点进行均值漂移聚类)
- 对象轮廓检验(光线传播算法)
- 目标跟踪(求解最优化Bhattacharya系数函数)
DBSCAN(基于密度的聚类方法)
全名Density-Based Spatial Clustering of Applications with Noise,是一个基于密度的聚类算法。
算法流程:
- 初始化,将所有数据点标记为未访问;
- 从任意一个未访问的数据点开始,定义一个当前簇,通过距离 ε提取邻域;
- 如果邻域中包含足够数量的点(根据minPoints),则聚类开始,将所有邻域中的点归入当前簇,否则标记为「噪声」。在这两种情况下,该点都被标记为「已访问」。
- 对当前簇中其它未访问的点,重复2、3;
- 完成当前簇的聚类后,再完成其它簇的聚类,重复2~4;
优点:自动发现簇的数量,自动发现异常值。
缺点:
- 如果样本集的密度不均匀、聚类间距差相差很大时,聚类质量较差。
这是因为当密度变化时,用于识别邻域点的距离阈值 ε 和 minPoints 的设置将会随着簇而变化。 - DBScan不能很好反映高维数据。
在高维数据中,距离阈值 ε 变得难以估计。
用高斯混合模型(GMM)的最大期望(EM)聚类
下图是K-Means的两个失败案例,K-Means 的一个主要缺点是它对于聚类中心均值的简单使用,不能处理簇中心接近的情况。GMM首先假设数据点符合高斯分布。

算法流程:
- 初始化,选择簇的数量(如 K-Means 所做的),随机初始化每个簇的高斯分布参数。也可以通过快速查看数据来尝试为初始参数提供一个好的猜测。
- 给定每个簇的高斯分布,计算每个数据点属于一个特定簇的概率。一个点越靠近高斯的中心,它就越可能属于该簇。
- 基于这些概率,使用EM的优化算法去更新每个簇的高斯分布参数(例如均值和标准差)。可以使用数据点位置的加权和来计算这些新参数,其中权重是数据点属于该特定簇的概率。
- 重复步骤 2 和 3 直到收敛,其中分布在迭代中的变化不大。
优点:
- GMMs 比 K-Means 在簇协方差方面更灵活;因为标准差参数,簇可以呈现任何椭圆形状,而不是被限制为圆形。K-Means 实际上是 GMM 的一个特殊情况,这种情况下每个簇的协方差在所有维度都接近 0。
- 因为 GMMs 使用概率,所以每个数据点可以有很多簇。因此如果一个数据点在两个重叠的簇的中间,我们可以简单地通过说它百分之 X 属于类 1,百分之 Y 属于类 2 来定义它的类。
凝聚层次聚类
通过合并的方式来聚类,停止条件决定了簇的个数。
算法流程:
- 初始化,我们首先将每个数据点视为一个单一的簇,即如果我们的数据集中有 X 个数据点,那么我们就有 X 个簇。计算每个簇之间的距离。
- 在每次迭代中,我们根据最短距离将两个簇合并成一个。
- 重新计算簇之间的距离。
- 重复步骤 2~3,直到只有一个包含所有数据点的簇。这样我们只需要选择何时停止合并簇,来选择最终需要多少个簇。
优点:
- 层次聚类不需要我们指定簇的数量,我们甚至可以选择哪个数量的簇看起来最好,因为我们正在构建一棵树;
- 对于距离度量标准的选择并不敏感。
缺点:
- 层次聚类的这些优点是以较低的效率为代价的,因为它具有 O(n³) 的时间复杂度。
图团体检测(Graph Community Detection)
当我们的样本以及样本之间的关系可以被表示为一个网络或图(graph)时,可能存在这样的需求——我们想找出来网络中联系比较”紧密”的样本。
举个例子,在社交网站中,用户以及用户之间的好友关系可以表示成下面的无向图,图中的顶点表示每个用户,顶点之间的边表示用户是否为好友关系。
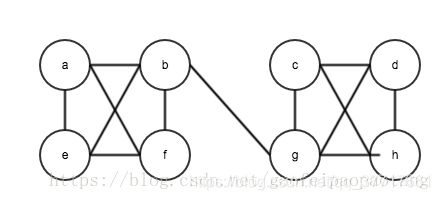
算法流程:
- 初始化,每个顶点自己的独自构成一个聚类,然后计算整个网络的模块性M;
- 尝试选择两个聚类融合到了一起,计算由此造成的模块性改变ΔM。
- 取ΔM出现了最大增长的两个聚类进行融合。然后为这个聚类计算新的模块性 M,并记录下来。
- 不断重复第2步和第3步,每一次都融合一对聚类,得到ΔM的最大增益,然后记录新的聚类模式及其相应的模块性M。
- 直到所有的顶点都被分组成了一个聚类时为止。然后该算法会检查这个聚类过程中的所有记录,然后找到其中返回了最高M值的聚类模式,这就是算法得到的聚类结构。
解释模块性:
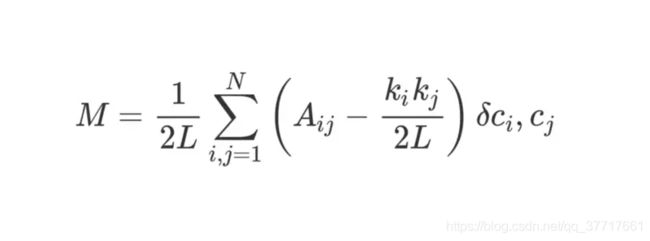
L表示图包含的边的数量,N表示顶点数量,ki表示顶点i的度(degree),Aij的值为邻接矩阵中的值(真实情况下存在连接为1,否则为0),ci表示顶点i的聚类,δ则是克罗内克函数(Kronecker-delta function)。
克罗内克函数δ的逻辑很简单,两个参数相等则返回1,不等则返回0。所以如果顶点i,j属于同一聚类,则δ(ci,cj)返回1,否则返回0。
ki*kj/2L可以理解为当该网络是随机分配的时候顶点i和j之间的预期边数,当ki,kj都比较小的时候,连接顶点i,j的边出现的概率就越小,描述两个顶点关系准确性也高。
Aij−ki*kj/2L可以理解为网络的真实结构和随机组合时的预期结构之间的差。研究它的值可以发现,当 Aij=1且 ki*kj/2L很小时,其返回的值最高。这意味着,当在顶点i和j之间存在连接,但是i, j之间存在连接的预期又比较小的时候,得到的值更高。再有,如果把这样的两个顶点分到一个聚类,则能提高网络的模块性。
优点:在典型的结构化数据中和现实网状数据都有非常好的性能。
缺点:它的局限性主要体现在会忽略一些小的集群,且只适用于结构化的图模型。
Ref
数据科学家必须了解的六大聚类算法:带你发现数据之美
均值漂移(Meanshift)算法
GMM公式+代码
GMM算法k-means算法的比较