吴恩达《机器学习》——SVM支持向量机

数据集、源文件可以在Github项目中获得
链接: https://github.com/Raymond-Yang-2001/AndrewNg-Machine-Learing-Homework

1. 线性SVM

1.1 从Logistic回归出发

在Logistic回归进行分类的时候，我们有$h_{\theta }(x)=\sigma ({\theta }^{\top }x)$，其中$\sigma$代表了sigmoid函数。Logisit回归在进行分类的时候，会使得正类的${\theta }^{\top }x\ge 0$，负类的${\theta }^{\top }x<0$。其损失函数如下：
$$J(\theta )=\sum _{i=1}^m-y^{(i)}\log (h_{\theta }(x^{(i)}))-(1-y^{(i)})\log (1-h_{\theta }(x^{(i)}))$$
其中，$-\log h_{\theta }(x)$和$-\log (1-h_{\theta }(x))$的函数图像如下所示：

对损失函数做如下修改，使得在$y=1$的时候，期望的${\theta }^{\top }x\gg 1$而不是${\theta }^{\top }x\gg 0$；在$y=0$的时候，期望的${\theta }^{\top }x\ll -1$而不是${\theta }^{\top }x\ll 0$。

这就得到了线性SVM的一般损失函数：
$$J(\theta )=C\sum _{i=1}^m[y^{(i)}{\mathrm{cost}}_1({\theta }^{\top }x)+(1-y^{(i)}){\mathrm{cost}}_0({\theta }^{\top }x)]+\frac{1}{2}\sum _{j=1}^n{\theta }_j^2$$
这里的C是正则化参数。

在线性SVM中，区别于Logistic回归输出分类概率，我们假设：
$$\{\begin{array}{rl}& h_{\theta }(x)=1,{\theta }^{\top }x\ge 0\\ & h_{\theta }(x)=0,\mathrm{else}\end{array}$$
也就是说，SVM分类器直接输出分类结果。

1.2 大边界分类与SVM

前文所述，在SVM中，最小化代价函数的必要条件是，在$y=1$的时候，期望的${\theta }^{\top }x\ge 1$而不是${\theta }^{\top }x\ge 0$；在$y=0$的时候，期望的${\theta }^{\top }x\ll -1$而不是${\theta }^{\top }x<0$。事实上，使用0作为分类边界已经能很好的区分进行分类了，SVM将这个分类边界进一步“加宽”，从0变成了(-1,1)，我们将SVM称作一种大边界的分类器。

考虑线性SVM的损失函数，假设我们找到了符合上述条件的$\theta$，那么在任何情况下，损失函数的前半部分都为0，也就是说优化目标可以简化为：
$$\begin{gathered} \min \frac{1}{2}\sum _{j=1}^n{\theta }_j^2=\frac{1}{2}||\theta |{|}^2 \\ s.t.\{\begin{array}{rl}& {\theta }^{\top }{x}^{(i)}\ge 1,y^{(i)}=1\\ & {\theta }^{\top }{x}^{(i)}\le -1,y^{(i)}=0\end{array} \end{gathered}$$

由线性代数知识可知：${\theta }^{\top }{x}^{(i)}={\rho }^{(i)}||\theta ||$，${\rho }^{(i)}$是$x^{(i)}$在$\theta$方向上的投影长度。
设我们的一种决策边界如下，蓝色线是$\theta$方向，与其垂直的绿色线是决策边界：

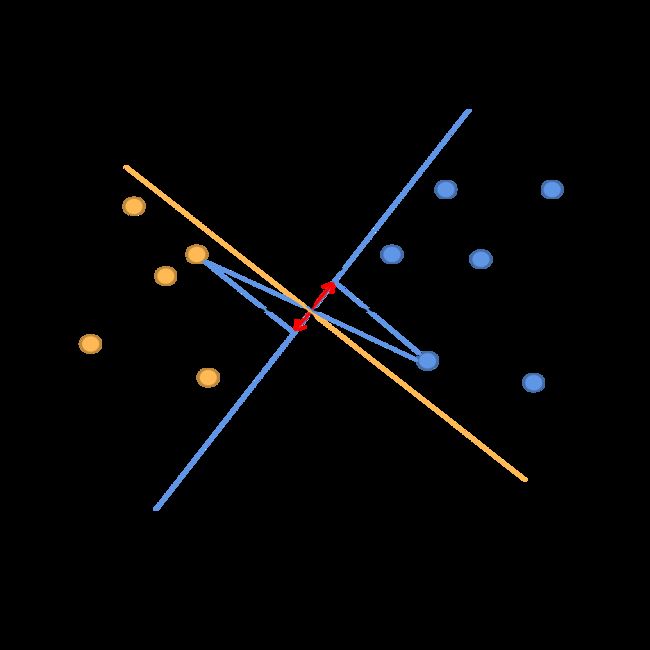
在这种情况下，$\rho$比较小，为了满足${\rho }^{(i)}||\theta ||\ge 1$或者${\rho }^{(i)}||\theta ||\le -1$，$||\theta ||$要变得很大才可以满足。显然，这会使得损失函数值变大，与优化目标相反。

考虑另一种决策边界：

在这种情况下，$\rho$会变大，相应的$||\theta ||$可以变得比较小。通过让间距变大，即通过这些$\rho$等等的值，支持向量机最终可以找到一个较小的范数。这正是支持向量机中最小化目标函数的目的，也就是为什么支持向量机最终会找到大间距分类器的原因。因为它试图极大化这些$\rho$的范数，它们是训练样本到决策边界的距离。

1.3 调整正则化参数

使用的数据集可视化如下：

使用正则化参数C=1

from sklearn import svm
svc = svm.LinearSVC(C=1, max_iter=1000)
svc.fit(x,y.ravel())
theta1 = [svc.intercept_[0], svc.coef_[0,0], svc.coef_[0,1]]

x_ax = np.arange(0, 4, 0.1)
xx = np.array([1.5,2.5])
y_ax = -theta1[0] / theta1[2] + (-theta1[1] / theta1[2])*x_ax
print(theta1[0],-theta1[0] / theta1[2],-theta1[1] / theta1[2])
yy = (theta1[2] / theta1[1] )*xx
plt.figure(figsize=(10,8))
plt.scatter(x=positive_data[:, 0], y=positive_data[:, 1], s=10, color="red",label="positive")
plt.scatter(x=negative_data[:, 0], y=negative_data[:, 1], s=10, label="negative")
plt.plot(x_ax, y_ax, label="Decision Boundary")
plt.plot(xx, yy, label="Direction of Theta Vector")
plt.axis('equal')
plt.legend(loc='best',framealpha=0.5)
plt.show()

可以看到SVM学习到了一个较好的分类器，没有受到左上角异常值的影响。

正则化参数C=1000

from sklearn import svm
svc2 = svm.LinearSVC(C=100, max_iter=100000)
svc2.fit(x,y.ravel())
theta2 = [svc2.intercept_[0], svc2.coef_[0,0], svc2.coef_[0,1]]
x_ax = np.arange(0, 4, 0.1)

y_ax = -theta2[0] / theta2[2] + (-theta2[1] / theta2[2])*x_ax

plt.figure(figsize=(10,8))
plt.scatter(x=positive_data[:, 0], y=positive_data[:, 1], s=10, color="red",label="positive")
plt.scatter(x=negative_data[:, 0], y=negative_data[:, 1], s=10, label="negative")
plt.plot(x_ax, y_ax, label="Decision Boundary")

xx = np.array([1,1.5])
yy = (theta2[2] / theta2[1] )*xx
plt.plot(xx + 1, yy, label="Direction of Theta Vector")

plt.axis('equal')
plt.legend(loc=0,framealpha=0.5)
plt.show()

可以看到，在C较大的情况下，SVM受到了离群值的影响，出现了过拟合的现象。

2. 非线性SVM（高斯核函数）

之前讨论的线性SVM，其优化目标的计算是基于${\theta }^{\top }x$的线性运算，当我们面对较复杂的决策边界的时候，简单的线性运算并不能很好的满足需求。就像在神经网络中引入非线性的激励函数一样，在SVM中，我们也引入非线性的核函数，来实现更复杂的分类。这类SVM叫做非线性SVM。

这相当于使用一系列新的特征来代替原样本，核函数就完成了样本到新特征的非线性映射。
$$f^{(i)}\leftarrow x^{(i)}$$

2.1 高斯核

$$f_i=sim(x,l^{(i)})=\exp \left(-\frac{||x-l^{(i)}|{|}^2}{2{\sigma }^2}\right)$$
当$x,l^{(i)}$相接近的时候，核函数值会接近1；当二者相距比较远的是时候，核函数值会接近0。
f ( i ) = ∣ f 0 ( i ) = 1 f 1 ( i ) = s i m ( x ( i ) , l ( 1 ) ) ⋮ f m ( i ) = s i m ( x ( i ) , l ( m ) ) ∣ f^{(i)}=\left|\begin{aligned} f^{(i)}_{0}&=1 \\ f^{(i)}_{1}=&sim(x^{(i)},l^{(1)}) \\ \vdots&\\ f^{(i)}_{m}=&sim(x^{(i)},l^{(m)}) \end{aligned} \right| f(i)= ​f0(i)​f1(i)​=⋮fm(i)​=​=1sim(x(i),l(1))sim(x(i),l(m))​ ​

优化目标函数变为：
$$J(\theta )=C\sum _{i=1}^m[y^{(i)}{\mathrm{cost}}_1({\theta }^{\top }{f}^{(i)})+(1-y^{(i)}){\mathrm{cost}}_0({\theta }^{\top }{f}^{(i)})]+\frac{1}{2}\sum _{j=1}^n{\theta }_j^2$$

当$\sigma$参数较大的时候，特征会变得更加平滑（$||x-l^{(i)}|{|}^2$的大小的变化对函数值的变化影响较小），不同样本的区分度会变小，这有利于缓解某些离群点的影响，使得模型的方差变小，减轻过拟合，但是会带来模型的偏差变大；相反，当$\sigma$参数较小的时候，特征会变得区分度更大，使得模型方差变大，偏差减小。

2.2 非线性分类

进行非线性分类的数据集可视化如下所示：

正则化参数为100

def show_boundary(svc, scale, fig_size, fig_dpi, positive_data, negative_data, term):
    """
    Show SVM classification boundary plot
    :param svc: instance of SVC, fitted and probability=True
    :param scale: scale for x-axis and y-axis
    :param fig_size: figure size, tuple (w, h)
    :param fig_dpi: figure dpi, int
    :param positive_data: positive data for dataset (n, d)
    :param negative_data: negative data for dataset (n, d)
    :param term: width for classification boundary
    :return: decision plot
    """
    t1 = np.linspace(scale[0, 0], scale[0, 1], 500)
    t2 = np.linspace(scale[1, 0], scale[1, 1], 500)
    coordinates = np.array([[x, y] for x in t1 for y in t2])
    prob = svc.predict_proba(coordinates)
    idx1 = np.where(np.logical_and(prob[:, 1] > 0.5 - term, prob[:, 1] < 0.5 + term))[0]
    my_bd = coordinates[idx1]
    plt.figure(figsize=fig_size, dpi=fig_dpi)
    plt.scatter(x=my_bd[:, 0], y=my_bd[:, 1], s=10, color="yellow", label="My Decision Boundary")
    plt.scatter(x=positive_data[:, 0], y=positive_data[:, 1], s=10, color="red", label="positive")
    plt.scatter(x=negative_data[:, 0], y=negative_data[:, 1], s=10, label="negative")
    plt.title('Decision Boundary')
    plt.legend(loc=2)
    plt.show()

from sklearn import svm
from sklearn.metrics import classification_report
svc100 = svm.SVC(C=100, kernel='rbf', gamma=10, probability=True)
svc100.fit(x,y.ravel())
report100 = classification_report(svc100.predict(x),y,digits=4)
print(report100)
show_boundary(svc100, scale=np.array([[0,1],[0.4,1]]), fig_size=fig_size, fig_dpi=fig_dpi,positive_data=positive_data,negative_data=negative_data, term=1e-3)

              precision    recall  f1-score   support

           0     0.9791    0.9542    0.9665       393
           1     0.9625    0.9830    0.9726       470

    accuracy                         0.9699       863
   macro avg     0.9708    0.9686    0.9696       863
weighted avg     0.9701    0.9699    0.9698       863

正则化参数为1

svc1 = svm.SVC(C=1, kernel="rbf", gamma=10, probability=True)
svc1.fit(x,y.ravel())
report1 = classification_report(svc1.predict(x),y,digits=4)
print(report1)
show_boundary(svc1, scale=np.array([[0,1],[0.4,1]]), fig_size=fig_size, fig_dpi=fig_dpi,positive_data=positive_data,negative_data=negative_data, term=1e-3)

              precision    recall  f1-score   support

           0     0.8851    0.8582    0.8715       395
           1     0.8833    0.9060    0.8945       468

    accuracy                         0.8841       863
   macro avg     0.8842    0.8821    0.8830       863
weighted avg     0.8841    0.8841    0.8840       863

可以看到，在正则化参数变小的情况下，分类边界变得更加“平滑”。

2.3 参数搜索

在机器学习的应用之中，确定参数是关键的一步，不同的参数会使得算法呈现不同的性能。最常用的一个方法是进行网格搜索GridSearch。

在实现网格搜索之前，我们先介绍一种评估模型性能的方法——k折交叉验证。一般情况下，在训练模型的过程中，我们只从训练集中划分出固定的一部分作为验证集；k折交叉验证将训练集划分为k部分，模型训练k次，每次使用其中一个作为验证集，其余作为训练集，用在验证集上的平均评分来评估模型性能。这种方法能够更全面的考虑整个训练集的数据分布，往往比固定验证集更能体现模型的泛化能力。

网格搜索的步骤是：

1. 对于目标参数给出取值集合，多个参数会组成类似一个“网格”的结构
2. 对于每个参数值组合，进行k折交叉验证（在sklearn中，默认使用k=5）
3. 选取平均得分最高的参数组合作为最优参数组合

代码实现如下：

candidate = [0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30, 100]
parameters_grid = np.array([[c, gamma] for c in candidate for gamma in candidate])

score_list = []
from sklearn.svm import SVC
from SVM import show_boundary
from sklearn.model_selection import KFold
kf = KFold(n_splits=5)
for param in parameters_grid:
    score = []
    for tr_idx, test_idx in kf.split(train_x,train_y):
        tr_x,tr_y = train_x[tr_idx], train_y[tr_idx]
        test_x, test_y = train_x[test_idx], train_y[test_idx]

        svc = SVC(C=param[0], gamma=param[1], probability=True)
        svc.fit(tr_x, tr_y.ravel())
        score.append(svc.score(test_x, test_y.ravel()))
    score_list.append(score)

score_arr = np.array(score_list).mean(axis=1)
best_param = parameters_grid[np.argmax(score_arr)]
best_score = score_arr.max()
param_dict = {'C': best_param[0], 'gamma': best_param[1]}
best_svc = SVC(probability=True)
best_svc.set_params(**param_dict)
best_svc.fit(train_x,train_y.ravel())
print("Best parameters C={}, gamma={}, with average precision of {:.4f}".format(best_param[0], best_param[1], best_score))

Best parameters C=30.0, gamma=3.0, with average precision of 0.9244

使用sklearn进行验证

svc = SVC(probability=True)
parameters = {'C': candidate, 'gamma': candidate}
# default 5-fold
clf = GridSearchCV(svc, parameters, n_jobs=-1)
clf.fit(train_x,train_y.ravel())
print("SKlearn result: C={}, gamma={}".format(clf.best_params_.get('C'), clf.best_params_.get('gamma')))

SKlearn result: C=30, gamma=3

可视化数据集和分类边界