知识图谱 | 表示学习篇
知识图谱 | 表示学习篇
- 1 知识图谱表示的挑战
- 2 词的向量表示方法
- 3 知识图谱嵌入
-
- 3.1 概念
- 3.2 优缺点
- 4 知识图谱嵌入方法
-
- 4.1 转移距离模型—TransE及其变体
-
- 4.1.1 TransE
- 4.1.2 TransH
- 4.1.3 TransR
- 4.1.4 TransD
- 4.1.5 TransSparse
- 4.1.6 TransM
- 4.1.7 ManifoldE
- 4.1.8 TransF
- 4.1.9 TransA
- 4.2 转移距离模型—高斯嵌入
-
- 4.2.1 KG2E
- 4.2.2 TransG
- 4.3 其他距离模型
-
- 4.3.1 非结构化模型UM
- 4.3.2 结构化嵌入SE
- 4.4 语义匹配模型—RESCAL模型及其变体
-
- 4.4.1 RESCAL模型(双线性模型)
- 4.4.2 DistMult模型
- 4.4.3 HolE
- 4.4.4 ComplEx
- 4.4.5 ANALOGY
- 4.5 语义匹配模型—基于神经网络的匹配
-
- 4.5.1 语义匹配能量模型 (SME)
- 4.5.2 神经张量网络模型 (NTN)
- 4.5.3 多层感知机 (MLP)
- 4.5.4 神经关联模型 (NAM)
- 4.6 考虑附加信息的模型
- 5 知识图谱嵌入应用
- 6 知识图谱表示学习的实现
- 7 表示学习稳定性比较
- 8 参考
1 知识图谱表示的挑战
知识图谱目前表示大多还是以三元组的表示方法进行,这种基于离散符号的方法进行表达,问题主要有两个:
- 不能在计算机中表达相应语义层面的信息,也不能进行语义计算,对下游的一些应用并不友好。
- 数据具有一定的稀疏性。现实中的知识图谱无论是实体还是关系都有长尾分布的情况,即某一个实体或关系具有极少的实例样本,这会影响某些应用的准确率
那针对上述挑战,我们应该如何处理呢?对知识图谱进行向量表示则是一个不错的方法!
2 词的向量表示方法
在对知识图谱进行向量表示之前,我们先来看个基础的,即词用向量如何表示?主要分为两大类方法:

完整版内容之前小编也见一篇博客,具体可以点击下方链接查看:
- 深度学习 | Word2vec原理及应用
3 知识图谱嵌入
3.1 概念
将知识图谱中包括实体和关系的内容映射到连续向量空间方法的研究领域称为知识图谱嵌入,也被称为知识图谱的向量表示、知识图谱的表示学习、知识表示学习。
知识图谱嵌入方法的训练需要基于监督学习:h+r=t
3.2 优缺点
优点:
- 提高应用时的计算效率
- 增加了下游应用设计的多样性
- 将知识图谱嵌入作为下游应用的预训练向量输入
缺点:
- 主要是不同知识图谱嵌入方法会对应一些缺点~这个在接下来的方法介绍中会详细说明
4 知识图谱嵌入方法
知识图谱嵌入方法主要分为转移距离模型和语义匹配模型:
- 转移距离模型:将衡量向量化后的知识图谱中三元组的合理性问题,转化成后衡量头实体和尾实体的距离问题。使用基于距离的评分函数
- 语义匹配模型:注重挖掘向量化后实体和关系的潜在语义。使用基于相似度的评分函数
而转移距离模型进一步的又可以分为下面三大类:
- 转移距离模型—TransE及其变体
- 转移距离模型—高斯嵌入
- 其他距离模型
语义匹配模型进一步可以分为下面两大类:
- 语义匹配模型—RESCAL模型及其变体
- 语义匹配模型—基于神经网络的匹配
4.1 转移距离模型—TransE及其变体
平移距离模型利用基于距离的评分函数。通常是在通过关系进行翻译之后,用两个实体之间的距离来衡量一个事实的合理性。
最核心的思想就是 h+r=t
下面逐一进行介绍
4.1.1 TransE
思想:实体和关系都在同一空间,对于每一个三元组(h,r,t)TransE 希望:h+r=t
评分函数: f r ( h , t ) = − ∥ h + r − t ∥ 1 / 2 f_{r}(h, t)=-\|\mathbf{h}+\mathbf{r}-\mathbf{t}\|_{1 / 2} fr(h,t)=−∥h+r−t∥1/2
优点:简单直观~计算复杂度也不高
缺点:复杂关系例如,一对多 、 多对一 、多对多关系不适用。比如
- 美国-总统-拜登
- 美国-总统-特朗普
通过TransE会使得拜登和特朗普的向量很接近
4.1.2 TransH
思想:将每种关系建模为一个超平面,对于每一个三元组(h,r,t)将h和t都投影到该平面,基于投影后的实体再进行学习
评分函数: f r ( h , t ) = − ∥ h ⊥ + r − t ⊥ ∥ 1 / 2 f_{r}(h, t)=-\|\mathbf{h}_{\perp}+\mathbf{r}-\mathbf{t}_{\perp}\|_{1 / 2} fr(h,t)=−∥h⊥+r−t⊥∥1/2
其中: h ⊥ = h − w r ⊤ h w r , t ⊥ = t − w r ⊤ t w r \mathbf{h}_{\perp}=\mathbf{h}-\mathbf{w}_{r}^{\top} \mathbf{h} \mathbf{w}_{r}, \quad \mathbf{t}_{\perp}=\mathbf{t}-\mathbf{w}_{r}^{\top} \mathbf{t} \mathbf{w}_{r} h⊥=h−wr⊤hwr,t⊥=t−wr⊤twr
优点:解决了TransE在多元关系上的缺陷,可以让一个实体在不同的关系下拥有不同的表示
缺点:TransE TransH的实体和关系仍然在同一空间中,对于某些场景可能不适用~
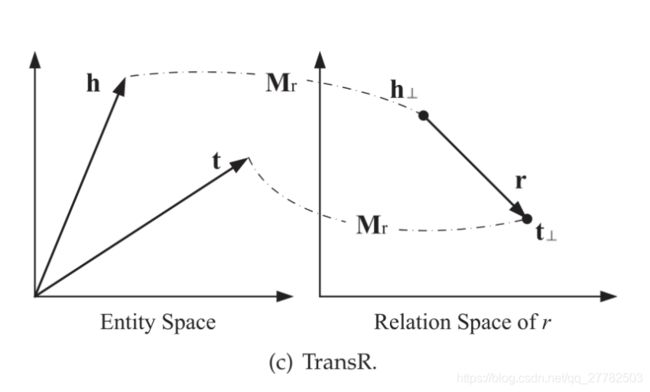
4.1.3 TransR
思想:TransR认为不同的关系应该有不同的语义空间,首先将实体映射到关系空间,然后再建立从头实体到尾实体的翻译关系
评分函数: f r ( h , t ) = − ∥ h ⊥ + r − t ⊥ ∥ 1 / 2 f_{r}(h, t)=-\|\mathbf{h}_{\perp}+\mathbf{r}-\mathbf{t}_{\perp}\|_{1 / 2} fr(h,t)=−∥h⊥+r−t⊥∥1/2
其中: h ⊥ = M r h , t ⊥ = M r t \mathbf{h}_{\perp}=\mathbf{M}_{r} \mathbf{h}, \quad \mathbf{t}_{\perp}=\mathbf{M}_{r} \mathbf{t} h⊥=Mrh,t⊥=Mrt
优点:解决了TransE TransH的实体和关系在同一空间中的缺陷,考虑到了实体和关系在不同空间中的情况~
缺点:
- 引入了空间映射,即矩阵 M r \mathbf{M}_{r} Mr,复杂度较高
- 同一个关系下头、尾实体共享相同的投影矩阵,有局限性,比如(美国,总统,奥巴马),美国和奥巴马的类型完全不同,一个是国家,一个是人物。
- TransR让投影矩阵仅与关系有关是不合理的,也可能和实体有关的
4.1.4 TransD
思想:将TransR的投影矩阵 M r \mathbf{M}_{r} Mr分解为两个投影矩阵,而这个投影矩阵与实体和关系向量都是相关的,投影后然后再建立从头实体到尾实体的翻译关系
评分函数: f r ( h , t ) = − ∥ h ⊥ + r − t ⊥ ∥ 1 / 2 f_{r}(h, t)=-\|\mathbf{h}_{\perp}+\mathbf{r}-\mathbf{t}_{\perp}\|_{1 / 2} fr(h,t)=−∥h⊥+r−t⊥∥1/2
其中: h ⊥ = M r h h , t ⊥ = M r t t \mathbf{h}_{\perp}=\mathbf{M}_{r}^{h} \mathbf{h}, \quad \mathbf{t}_{\perp}=\mathbf{M}_{r}^{t} \mathbf{t} h⊥=Mrhh,t⊥=Mrtt
两个投影矩阵见下:

优点:解决了在同一个关系下头、尾实体共享相同的投影矩阵问题,扩大了适用性
缺点:Trans系列模型的一些典型特点,具体下面介绍~
4.1.5 TransSparse
在投影矩阵上强化稀疏性来简化TransR,它有两个版本:TranSparse (共享)和TranSparse (单独)。
- TranSparse (共享):对每个关系r使用相同的稀疏投影矩阵
- TranSparse (单独):对于头实体和尾实体分别使用2个不同的投影矩阵
通过这种方式,可以减少模型的参数,降低复杂度~就是一个计算的Trick,思想是一致的,故不再赘述
4.1.6 TransM
思想:TransM放松TransE的转化要求,提高模型性能。具体是为每个三元组分配特定的关系权重θ(比如通过对一对多、多对一和多对多分配较小的权重,TransM模型使得t在上述的复杂关系中离h+r更远),改变评分函数。
评分函数: f r ( h , t ) = − θ r ∥ h + r − t ∥ 1 / 2 f_{r}(h, t)=-\theta_{r}\|\mathbf{h}+\mathbf{r}-\mathbf{t}\|_{1 / 2} fr(h,t)=−θr∥h+r−t∥1/2
优点:对于一对多、多对一和多对多这种复杂关系时学习效果较好~
缺点:对于没有复杂关系时学习效果可能会打折扣
4.1.7 ManifoldE
思想:把关系t近似地位于流形体上,即一个以h+r为中心半径为theta_r的超球体,而不是接近h+r的精确点,改变评分函数。
评分函数: f r ( h , t ) = − ( ∣ ∣ h + r − t ∥ 2 2 − θ r 2 ) 2 f_{r}(h, t)=-(||\mathbf{h}+\mathbf{r}-\mathbf{t}\|_{2}^{2}-\theta_{r}^2)^2 fr(h,t)=−(∣∣h+r−t∥22−θr2)2
优点:对于复杂关系时学习效果较好~
缺点:对于没有复杂关系时学习效果可能会打折扣
4.1.8 TransF
思想:TransF使用了类似ManifoldE的思想。不是执行严格的翻译h+r≈t,而是只需要t与h+r位于同一个方向,同时h与t-r也位于同一个方向。同样是通过改变评分函数的思路。
评分函数: f r ( h , t ) = ( h + r ) T t + ( t − r ) T h f_{r}(h, t)=(h+r)^{T}t+(t-r)^{T}h fr(h,t)=(h+r)Tt+(t−r)Th
优点:对于复杂关系时学习效果较好~
缺点:对于没有复杂关系时学习效果可能会打折扣
4.1.9 TransA
思想:TransA模型为每个关系r引入一个对称的非负矩阵Mr,并使用自适应马氏距离定义评分函数
评分函数: f r ( h , t ) = − ( ∣ h + r − t ∣ ) T M r ( ∣ h + t − r ∣ ) f_{r}(h, t)=-(|h+r-t|)^{T}M_{r}(|h+t-r|) fr(h,t)=−(∣h+r−t∣)TMr(∣h+t−r∣)
优点:
- 对于复杂关系时学习效果较好~
- 解决了上述TransE及其变体评分函数只采用L1或L2距离,灵活性不够的问题
- 解决了评分函数过于简单,实体和关系向量的每一维等同考虑的问题
缺点:对于没有复杂关系时学习效果可能会打折扣
4.2 转移距离模型—高斯嵌入
为什么会有转移距离模型?因为考虑到实体与关系的不确定性,使用随机变量进行建模!故引入高斯分布!
4.2.1 KG2E
思想:KG2E使用高斯分布来表示实体和关系,其中高斯分布的均值表示的是实体或关系在语义空间中的中心位置,而高斯分布的协方差则表示该实体或关系的不确定度。KG2E 模型将实体和关系表示为从多变量高斯分布中抽取的随机向量。
评分函数:
h ∼ N ( μ h , Σ h ) t ∼ N ( μ t , Σ t ) r ∼ N ( μ r , Σ r ) \begin{aligned} \mathbf{h} & \sim \mathcal{N}\left(\boldsymbol{\mu}_{h}, \Sigma_{h}\right) \\ \mathbf{t} & \sim \mathcal{N}\left(\boldsymbol{\mu}_{t}, \mathbf{\Sigma}_{t}\right) \\ \mathbf{r} & \sim \mathcal{N}\left(\boldsymbol{\mu}_{r}, \mathbf{\Sigma}_{r}\right) \end{aligned} htr∼N(μh,Σh)∼N(μt,Σt)∼N(μr,Σr)
通过测量 t-h 和 r 这两个随机向量之间的距离来为一个事实评分,具体是使用两种方法来进行测量:
- 通过 KL 散度(KL 距离)来进行测量
- 通过计算概率的内积
优点:
- KG2E可以有效地对知识图谱中实体和关系的不确定性进行建模
缺点:复杂度会比较高
4.2.2 TransG
思想:TransG是实体采用高斯分布来表示,但它认为关系具有多重语义(每种语义用一个高斯分布来刻画),需要采用混合的高斯分布的表示。
4.3 其他距离模型
4.3.1 非结构化模型UM
思想:TransE的简单版本,直接设置所有的r=0。
评分函数:
f r ( h , t ) = − ∥ h − t ∥ 2 2 f_{r}(h, t)=-\|\mathbf{h}-\mathbf{t}\|_{2}^{2} fr(h,t)=−∥h−t∥22
4.3.2 结构化嵌入SE
思想:通过使用两个独立的矩阵为每个关系 r 对头尾实体进行投影
评分函数:
f r ( h , t ) = − ∥ M r 1 h − M r 2 t ∥ 1 f_{r}(h, t)=-\left\|\mathbf{M}_{r}^{1} \mathbf{h}-\mathbf{M}_{r}^{2} \mathbf{t}\right\|_{1} fr(h,t)=−∥∥Mr1h−Mr2t∥∥1
4.4 语义匹配模型—RESCAL模型及其变体
语义匹配模型利用基于相似性的评分函数。
它们通过匹配实体的潜在语义和向量空间表示中包含的关系来度量事实的可信性。

4.4.1 RESCAL模型(双线性模型)
思想:实体用向量表示,关系用矩阵表示。该关系矩阵对潜在因素之间的成对交互作用进行了建模。评分函数是一个双线性函数。
评分函数:
f r ( h , t ) = h ⊤ M r t = ∑ i = 0 d − 1 ∑ j = 0 d − 1 [ M r ] i j ⋅ [ h ] i ⋅ [ t ] j f_{r}(h, t)=\mathbf{h}^{\top} \mathbf{M}_{r} \mathbf{t}=\sum_{i=0}^{d-1} \sum_{j=0}^{d-1}\left[\mathbf{M}_{r}\right]_{i j} \cdot[\mathbf{h}]_{i} \cdot[\mathbf{t}]_{j} fr(h,t)=h⊤Mrt=∑i=0d−1∑j=0d−1[Mr]ij⋅[h]i⋅[t]j
优点:
- RESCAL模型是基于向量相似性的模型,可以刻画实体和关系之间的二阶联系,效果比较好
缺点:参数较多,有一定复杂度
4.4.2 DistMult模型
思想:将上述RESCAL模型中的关系矩阵 M r {M}_{r} Mr简化为对角矩阵,其余不变。
评分函数:
f r ( h , t ) = h ⊤ M r t f_{r}(h, t)=\mathbf{h}^{\top} \mathbf{M}_{r} \mathbf{t} fr(h,t)=h⊤Mrt
优点:
- 降低复杂度,部分场景模型越简单效果可能越好
缺点:这种过度简化的模型只能处理对称的关系,这显然对于一般的KGs是不能完全适用的。
4.4.3 HolE
思想:HolE 将 RESCAL 的表达能力与 DistMult 的效率和简单性相结合。使用循环相关操作(circular correlation operation)
评分函数:
f r ( h , t ) = r T ( h ∗ t ) f_{r}(h, t)=\mathbf{r}^{T} (h * t) fr(h,t)=rT(h∗t)
优点:
- 结合了REACAL和DistMult各自的优点
4.4.4 ComplEx
思想:引入复数扩展DistMult,以便更好地对非对称关系进行建模。
此时,实体、关系都在复数空间,非对称关系的事实可以根据涉及实体的顺序得到不同的分数。每个 ComplEx 都有一个等价的 HolE,同时,如果在嵌入上施加共轭对称,那么,HolE是ComplEx的特殊情况。
4.4.5 ANALOGY
思想:ANALOGY 扩展了 RESCAL,从而进一步对实体和关系的类比属性进行建模。例如,A之于B,正如C之于D.
尽管 ANALOGY 表示关系为矩阵,这些矩阵可以同时对角化成一组稀疏的准对角矩阵。结果表明,前面介绍的 DistMult、HolE、ComplEx 等方法都可以归为 ANALOGY 的特例。
4.5 语义匹配模型—基于神经网络的匹配
4.5.1 语义匹配能量模型 (SME)
思想:首先将实体和关系投影到输入层中的嵌入向量,然后关系r与头尾实体分别组合至隐藏层。输出则是评分函数。
SME 有两个版本:线性版本和双线性版本。
4.5.2 神经张量网络模型 (NTN)
思想:
- 给定一个事实,它首先将实体投影到输入层中的嵌入向量。
- 然后,将这两个实体 h,t 由关系特有的关系张量(以及其他参数) 组合,并映射到一个非线性隐藏层。
- 最后,一个特定于关系的线性输出层给出了评分。
NTN是迄今为止最具表达能力的模型,但是参数过多,处理大型知识图谱效率较差。
4.5.3 多层感知机 (MLP)
思想:
MLP 是一种更简单的方法,在这种方法中,每个关系 (以及实体) 都是由一个向量组合而成的。给定一个事实,将嵌入向量 h、r 和 t 连接在输入层中,并映射到非线性的隐藏层。然后由线性输出层生成分数。
4.5.4 神经关联模型 (NAM)
思想:
给定一个事实,它首先将头实体的嵌入向量和输入层中的关系连接起来,在“deep”神经网络隐藏层的前馈过程之后,通过匹配最后一个隐藏层的输出和尾实体的嵌入向量来给出分数。
4.6 考虑附加信息的模型
目前介绍的方法仅使用KG中观察到的事实来执行嵌入任务。事实上,可以合并许多附加信息来进一步改进任务,例如实体类型、关系路径、文本描述以及逻辑规则。
附加信息1:实体类型,即实体所属的语义类别,将实体的类型作为一个三元组放入模型训练。比如香蕉是一种水果,可以将三元组香蕉-类型-水果放入模型训练。
附加信息2:文本描述的集成。比如在三元组中对两个实体有着很充分的文本描述,这时可以通过对文本进行学习得到词向量,进而得到两个实体的向量,作为初始值进行训练。
5 知识图谱嵌入应用
- 链接预测
- 三元组分类
- 实体对齐
- 问答系统
- 推荐系统
6 知识图谱表示学习的实现
在具体实现时,采用的是清华大学刘知远老师团队的OpenKE工具包,真的是非常好用!给刘老师点赞!具体链接为:https://github.com/thunlp/OpenKE
我当时硕士毕业论文涉及到网络表示学习的工作,也用到了刘老师团队的OpenNE。太棒了!
具体使用代码GitHub上都有实例,就不再赘述,目前OpenKE-PyTorch版本支持的模型有:
- RESCAL
- DistMult, ComplEx, Analogy
- TransE, TransH, TransR, TransD
- SimplE
- RotatE
在进行表示学习过程中,可以通过下述代码对表示学习结果进行存储:(以TransE为例)
transe.save_checkpoint('./checkpoint/transe.ckpt')
transe.save_parameters('./embed.vec') # 保存嵌入向量到该文件中
而对于上面表示学习结果的解析,可以使用下述代码:
import json
ent_rel_all_vec = open('embed.vec', 'r')
for file in ent_rel_all_vec:
new_dict = json.loads(file)
# 1.1 实体编号及向量表示
all_ent_vec = new_dict['ent_embeddings.weight']
print('向量维度为 %d' % len(all_ent_vec[0]))
# 1.2 关系编号及向量表示
all_rel_vec = new_dict['rel_embeddings.weight']
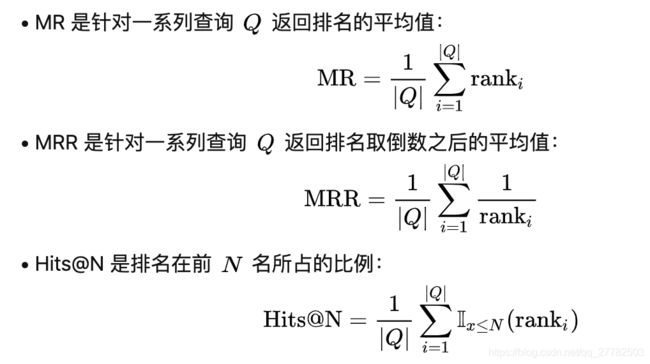
在表示学习结束后,需要进行评估,具体相关的指标见下图:

评估思想:
- link prediction任务:用于预测三元组中缺失的关系或者尾实体,对于测试的三元组,我们replace掉了head/tail 实体,并以降序的顺序给出预测出实体的得分。平均的指标有:
- MR:正确实体的平均rank。
- MRR: the average of the reciprocal ranks of correct entities。
- Hit@N:正确实体在top-N的比率
- 其中排名-涉及总排名就是指所有实体的个数,因为对于一个测试三元组,会替换这个头或尾实体,是用所有实体去替换的!然后看每一个正确的测试三元组是否在排名前10/3/1,是的话就+1;对于MR和MRR就是直接看正确三元组在所有的三元组(用所有实体去替换尾实体后的)中排名
- 因为某些伪例三元组可能在训练集中和验证集中。在这种情况下,那些伪例三元组可能会排在测试三元组之上,但这不应被视为错误,因为两个三元组都应该是正确的。因此,OPENKE删除了出现在训练,验证或测试集中的那些伪例三元组,从而确保伪例三元组不在数据集中。即Filter的结果—即修复后的结果!
- 上述目的是为了评估embedding的效果!如何评估?采用对测试三元组进行随机替换头部或者尾部实体!然后如果embedding效果比较好,那么原始(没有替换时)三元组得分是低的(也就是满足翻译关系,h+r=t),打乱后的三元组得分很高,那么很多三元组进行混合之后,从小到大进行排序,计算前10/3/1中正确的实体(原始的)比例,即可反映embedding的效果!越大越好!
- 对于那些大型实体集,使用整个实体集破坏所有实体是费时的。因此,OPENKE还为具有某些受其关系确定的有限实体集的损坏实体提供了名为type-constrain的实验设置。
7 表示学习稳定性比较
思路:表示学习每次结果是否稳定呢?一种最朴素的思路就是训练多次,通过计算每次向量余弦相似度TopN中重复的实体个数。重复比例越大,那么表示学习稳定性就越好~
8 参考
- 融合事实信息的知识图谱嵌入——翻译距离模型
- 融合事实信息的知识图谱嵌入——语义匹配模型
- 知识图谱嵌入(KGE):方法和应用的综述
- 知识表示学习(知识表征)