手把手实现邮件分类 《Getting Started with NLP》chap2：Your first NLP example

《Getting Started with NLP》chap2：Your first NLP example

感觉这本书很适合我这种菜菜,另外下面的笔记还有学习英语的目的，故大多数用英文摘录或总结

• This chapter covers
  • Implementing your first practical NLP application from scratch
  • Structuring an NLP project from beginning to end
  • Exploring NLP concepts, including tokenization and text normalization
  • Applying a machine learning algorithm to textual data

昨天刚在《机器学习实战》那本书里面看了以spam filtering为例子贯穿讲解的ML的landscape，今天就来跟着这个chapter实践一下

2.1 Introducing NLP in practice: Spam filtering

• Spam filtering exemplifies a widely spread family of tasks —— text classification.

  exemplify :to be or give a typical example of something 作为…的典范（或范例、典型、榜样等）

classification

• 作者给了很多非常贴近生活的例子 ~ 讲了 classification的usefulness，概括一下

  • Classification helps us reason about things and adjust our behavior based on them.
  • Classification allows us to group things into categories, making it easier to deal with individual instances.

• We refer to the name of each class as a class label

  • When we are dealing with two labels only, it is called binary classification
  • Classification that implies more than two classes is called multiclass classification

• How do we perform classification ?

  • Classification is performed based on certain characteristics or features of the concepts being classified.
  • The specific characteristics or features used in classification depend on the task at hand.
  • In machine-learning terms, we call such characteristics “features”.

---

• 作者给了一段summary
  • Classification refers to the process of identifying which category or class among the set of categories (classes) an observation belongs to based on its properties. In machine learning, such properties are called features and the class names are called class labels. If you classify observations into two classes, you are dealing with binary classification; tasks with more than two classes are examples of multiclass classification.

---

一个简单的例子

其实大一最早的时候做的经典的老掉牙if/else或者那个switch，输入学生成绩，给出成绩，就是simple classification

这里作者也给出了很simple的程序

For example, you can make the machine print out a warning that water is hot based on a simple threshold of 45°C (113°F), as listing 2.1 suggests. In this code, you define a function print_warning, which takes water temperature as input and prints out water status. The if statement checks if input temperature is above a predefined threshold（阈值） and prints out a warning message if it is. In this case, since the temperature is above 45°C, the code prints out Caution: Hot water!

#  Simple code to tell whether water is cold or hot
def print_warning(temperature): 
    if temperature>=45: 
        print ("Caution: Hot water!")
    else:
        print ("You may use water as usual")
print_warning(46) 

感觉写的不错，作者把这个例子过渡到了ML 和 监督学习

When there are multiple factors to consider in classification, it is better to let the machine learn the rules and patterns from data rather than hardcoding（写死） them. Machine learning involves providing a machine with examples and a general outline of a task, and allowing it to learn to solve the task independently. In supervised machine learning, the machine is given labeled data and learns to classify based on the provided features.

Supervised machine learning

Supervised machine learning refers to a family of machine-learning tasks in which the algorithm learns the correspondences between an input and an output based on the provided labeled examples. Classification is an example of a supervised machine learning task, where the algorithm tries to learn the mapping between the input data and the output class label.

Using the cold or hot water example, we can provide the machine with the samples of water labeled hot and samples of water labeled cold, tell it to use temperature as the predictive factor (feature), and this way let it learn independently from the provided data that the boundary between the two classes is around 45°C (113°F)

2.2 Understanding the task

作者给出了scenario （a description of possible actions or events in the future可能发生的事态；设想）

Consider the following scenario: you have a collection of spam and normal emails from the past. You are tasked with building a spam filter, which for any future incoming email can predict whether this email is spam or not. Consider these questions:

• How can you use the provided data?
• What characteristics of the emails might be particularly useful, and how will you extract them?
• What will be the sequence of steps in this application?

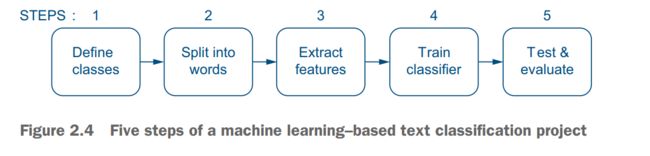
In this section, we will discuss this scenario and look into the implementation steps. In total, the pipeline for this task will consist of five steps.

The pipeline

Step 1: Define the data and classes

“normal” emails are sometimes called “ham” in the spam-detection context

First, you need to ask yourself what format the email messages are delivered in for this task. For instance, in a real-life situation, you might need to extract the messages from the mail agent application. However, for simplicity, let’s assume that someone has extracted the emails for you and stored them in text format. The normal emails are stored in a separate folder—let’s call it Ham, and spam emails are stored in a Spam folder.

If someone has already predefined past spam and ham emails for you (e.g., by extracting these emails from the INBOX and SPAM box), you don’t need to bother with labeling them. However, you still need to point the machine-learning algorithm at the two folders by clearly defining which one is ham and which one is spam. This way, you will define the class labels and identify the number of classes for the algorithm. This should be the first step in your spam-detection pipeline (and in any text-classification pipeline), after which you can preprocess the data, extract the relevant information, and then train and test your algorithm (figure 2.5).

You can set step 1 of your algorithm as follows: Define which data represents “ham” class and which data represents “spam” class for the machine-learning algorithm.

Step 2: Split the text into words

• Next, you will need to define the features for the machine to know what type of information, or what properties of the emails to pay attention to, but before you can do that, there is one more step to perform – split the text into words.

为何需要split into words?

• The content of an email can be useful for identifying spam, but using the entire email as a single feature may not work well because even small changes can affect it. Instead, smaller chunks of text like individual words might be more effective features because they are more likely to carry spam-related information and are repetitive enough to appear in multiple emails.

如何split into words(exercise 2.2)

• For a machine, the text comes in as a sequence of symbols, so the machine does not have an idea of what a word is.

  • How would you define what a word is from the human perspective?
  • How would you code this for a machine?

  For example, how will you split the following sentence into words? “Define which data represents each class for the machine learning algorithm.”

split text string into words by whitespaces

• The first solution might be “Words are sequences of characters separated by whitespaces.”

• simple code to split text string into words by whitespaces

  text = "Define which data represents each class for the machine learning algorithm"
  text.split(" ")
  

  ['Define',
   'which',
   'data',
   'represents',
   'each',
   'class',
   'for',
   'the',
   'machine',
   'learning',
   'algorithm']
  

• So far(到目前为止), so good. However, what happens to this strategy when we have punctuation marks? For example: “Define which data represents “ham” class and which data represents “spam” class for the machine learning algorithm.”

  ['Define',
   'which',
   'data',
   'represents',
   '“ham”',
   'class',
   'and',
   'which',
   'data',
   'represents',
   '“spam”',
   'class',
   'for',
   'the',
   'machine',
   'learning',
   'algorithm.']
  

  In the list of words, are [“ham”], [“spam”], and [algorithm.] any different from [ham], [spam], and [algorithm]? That is, the same words but without the punctuation marks attached to them? The answer is, these words are exactly the same, but because you are only splitting by whitespaces at the moment, there is no way of taking the punctuation marks into account.

  However, each sentence will likely include one full stop (.), question (?), or exclamation mark (!) attached to the last word, and possibly more punctuation marks inside the sentence itself, so this is going to be a problem for properly extracting words from text. Ideally, you would like to be able to extract words and punctuation marks separately.

split text string into words by whitespaces and punctuation

• 那么如何把标点符号punctuation考虑进来？ 书上给出了很详细的算法描述！

1. Store words list and a variable that keeps track of the current word—let’s call it current_word for simplicity.
2. Read text character by character:
   • If a character is a whitespace, add the current_word to the words list and update the current_word variable to be ready to start a new word.
   • Else if a character is a punctuation mark:
     • If the previous character is not a whitespace, add the current_word to the words list; then add the punctuation mark as a separate word token, and update the current_word variable.
     • Else if the previous character is a whitespace, just add the punctuation mark as a separate word token.
   • Else if a character is a letter other than a whitespace or punctuation mark, add it to the current_word.

orz，感觉这图做得很好

• Code to split text string into words by whitespaces and punctuation

  delimiter 分隔符，定界符

  text = "Define which data represents “ham” class and which data represents “spam” class for the machine learning algorithm."
  delimiters = ['"', "."]
  words = []
  current_word = ""
  for char in text:
      if char==" ":
          if not current_word=="":
              words.append(current_word)
              current_word = ""
      elif char in delimiters:
          if current_word=="":  #current_word是空的说明前面一个是whitespace，只把标点加入list
              words.append(char)
          else:
              words.append(current_word)
              words.append(char)
              current_word = ""
      else:
          current_word += char
  
  print(words)
  

  ['Define', 'which', 'data', 'represents', '“ham”', 'class', 'and', 'which', 'data', 'represents', '“spam”', 'class', 'for', 'the', 'machine', 'learning', 'algorithm', '.']
  

• 这个时候完美了吗? 没有， 有很多时候我们用的缩写比如e.g.,i.e.是不需要拆的 ，但是用刚刚的算法会拆成[‘i’,‘.’,‘e’,'.]

tokenizers

• This is problematic, since if the algorithm splits these examples in this way, it will lose track of the correct interpretation of words like i.e. or U.S.A., which should be treated as one word token rather than a combination of characters. How can this be achieved?

• This is where the NLP tools come in handy: the tool that helps you split the running string of characters into meaningful words is called tokenizer, and it takes care of the cases like the ones we’ve just discussed—that is, it can recognize that ham. needs to be split into [‘ham’, ‘.’] while U.S.A. needs to be kept as one word [‘U.S.A.’]. Normally, tokenizers rely on extensive and carefully designed lists of regular expressions, and some are trained using machine-learning approaches.

• 这里作者介绍了NLTK

  For an example of a regular expressions-based tokenizer, you can check the Natural Language Processing Toolkit’s regexp_tokenize() to get a general idea of the types of the rules that tokenizers take into account: see Section 3.7 on www.nltk.org/book/ch03.html. The lists of rules applied may differ from one tokenizer to another.

• tokenizer还可以给我们解决哪些常见的problem呢？ 缩写（contraction）

  看几个例子

  • What’s the best way to cook a pizza?
    • The first bit, What’s, should also be split into two words: this is a contraction for what and is, and it is important that the classifier knows that these two are separate words. Therefore, the word list for this sentence will include [What, 's, the, best, way, to, cook, a, pizza, ?].
  • We’re going to use a baking stone.
    • we’re should be split into we and 're (“are”). Therefore, the full word list will be [We, 're, going, to, use, a, baking, stone, .].
  • I haven’t used a baking stone before.
    • [I, have, n’t, used, a, baking, stone, before, .]. Note that the contraction of have and not here results in an apostrophe inside the word not; however, you should still be able to recognize that the proper English words in this sequence are have and n’t (“not”) rather than haven and 't. This is what the tokenizer will automatically do for you. (Note that the tokenizers do not automatically map contracted forms like n’t and ’re to full form like not and are. Although such mapping would be useful in some cases, this is beyond the functionality of tokenizers.)

  如何解决这个呢，正则表达式是一个神奇的东西

  import nltk
  import re
  
  text1 = "What’s the best way to cook a pizza?"
  text2 = "We’re going to use a baking stone."
  text3 = "I haven’t used a baking stone before."
  
  texts = [text1, text2, text3]
  
  tokens = []
  for text in texts:
    # Replace certain characters with a space
    text = re.sub(r'[’]', '\'', text)
    print(text)
    # text = re.sub(r'[^\w\s\.\?\']', ' ', text)
    # print(text)
    # Tokenize the text
    tokens.append(nltk.word_tokenize(text))
  
  for token in tokens:
    print(token)
  # print(tokens)
  
  

  What's the best way to cook a pizza?
  We're going to use a baking stone.
  I haven't used a baking stone before.
  ['What', "'s", 'the', 'best', 'way', 'to', 'cook', 'a', 'pizza', '?']
  ['We', "'re", 'going', 'to', 'use', 'a', 'baking', 'stone', '.']
  ['I', 'have', "n't", 'used', 'a', 'baking', 'stone', 'before', '.']
  

Step 3: Extract and normalize the features

• 作者举了个例子

  • Suppose two emails use a different format:

    • one says Collect your lottery winnings
    • while another one says Collect Your Lottery Winnings

    拆开的词语里面 lottery 和 Lottery 形式上确实不同，但是意思上是一样的，都是博彩

  我们需要get rid of such formatting issues

• The problem is that small formatting differences, such as the use of uppercase versus lowercase letters, can result in different word lists being generated. To address this issue, the passage suggests normalizing the extracted words by converting them to lowercase. This can help ensure that the meaning of the words is not affected by formatting differences and that the extracted words are more indicative（标示的） of the spam-related content of the emails.

Step 4: Train a classifier

• At this point, you will end up with two sets of data—one linked to the spam class and another one linked to the ham class. Each data is preprocessed in the same way in steps 2 and 3, and the features are extracted.

• Next, you need to let the machine use this data to build the connection between the set of features (properties) that describe each type of email (spam or ham) and the labels attached to each type. In step 4, a machine-learning algorithm tries to build a statistical model, a function, that helps it distinguish between the two classes. This is what happens during the learning (training) phase（阶段）.

• A refresher visualizing the training and test processes.

  

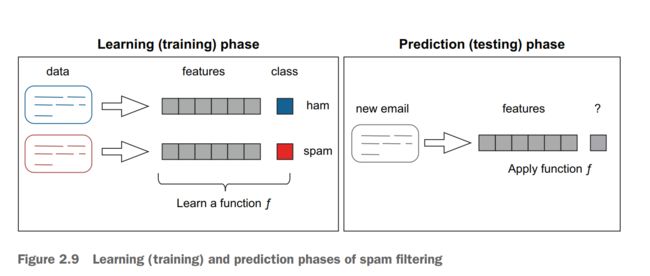
• So, step 4 of the algorithm should be defined as follows: define a machine-learning model and train it on the data with the features predefined in the previous steps

• Suppose that the algorithm has learned to map the features of each class of emails to the spam and ham labels, and has determined which features are more indicative of spam or ham. The final step in this process is to make sure the algorithm is doing such predictions well.

• How will you do that? 划分数据集

• The data used for training and testing should be chosen randomly and should not overlap（交叠） in order to avoid biasing the evaluation. The training set is typically larger, with a typical proportion being 80% for training and 20% for testing. The classifier should not be allowed to access the test set during the training phase, and it should only be used for evaluation at the final step.

shuffle 洗牌

Data splits for supervised machine learning

In supervised machine learning, the algorithm is trained on a subset of the labeled data called training set. It uses this subset to learn the function mapping the input data to the output labels. Test set is the subset of the data, disjointed（分离） from the training set, on which the algorithm can then be evaluated. The typical data split is 80% for training and 20% for testing. Note that it is important that the two sets are not overlapping. If your algorithm is trained and tested on the same data, you won’t be able to tell what it actually learned rather than memorized.

Step 5: Evaluate the classifier

• Suppose you trained your classifier in step 4 and then applied it to the test data. How will you measure the performance?

• One approach would be to check what proportion of the test emails the algorithm classifies correctly—that is, assigns the spam label to a spam email and classifies ham emails as ham. This proportion is called accuracy, and its calculation is pretty straightforward:
  $$Accuracy=\frac{num(\text{ correct predictions })}{num(\text{ all test instances })}$$

• 这里给了个练习2.4

  

  Let’s discuss the solutions to this exercise (note that you can also find more detailed explanations at the end of the chapter). The prediction of the classifier based on the distribution of classes that you came across in this exercise is called baseline. In an equal class distribution case, the baseline is 50%, and if your classifier yields an accuracy of 60%, it outperforms this baseline. In the case of 60:40 split, the baseline, which can also be called the majority class baseline, is 60%. This means that if a dummy “classifier” does no learning at all and simply predicts the ham label for all emails, it will not filter out any spam emails from the inbox, but its accuracy will also be 60%—just like your classifier that is actually trained and performs some classification! This makes the classifier in the second case in this exercise much less useful because it does not outperform the majority class baseline.

  书后给的解答

  2. An accuracy of 60% doesn’t seem very high, but how exactly can you interpret it? Note that the distribution of classes helps you to put the performance of your classifier in context because it tells you how challenging the problem itself is. For example, with the 50–50% split, there is no majority class in the data and the classifier’s random guess will be at 50%, so the classifier’s accuracy is higher than this random guess. In the second case, however, the classifier performs on a par with the majority class guesser: the 60% to 40% distribution of classes suggests that if some dummy “classifier” always selected the majority class, it would get 60% of the cases correctly—just like the classifier you trained.
  3. The single accuracy value of 60% does not tell you anything about the performance of the classifier on each class, so it is a bit hard to interpret. However, if you look into each class separately, you can tell that the classifier is better at classifying ham emails (it got 2/3 of those right) than at classifying spam emails (only 1/2 are correct).

• In summary, accuracy is a good overall measure of performance, but you need to keep in mind

  • (1) the distribution of classes to have a comparison point for the classifier’s performance
  • (2) the performance on each class, which is hidden within a single accuracy value but might suggest what the strengths and weaknesses of your classifier are. Therefore, the final step, step 5, in your algorithm is applying your classifier to the test data and evaluating its performance

2.3 Implementing your own spam filter

Step 1: Define the data and classes

• 数据集：Enron Email Dataset (cmu.edu)
  • This is a dataset of emails, including both ham (extracted from the original Enron dataset using personal messages of three Enron employees) and spam emails. To make processing more manageable, we will use a subset of this large dataset.
  • All folders in the Enron dataset contain spam and ham emails in separate subfolders. Each email is stored as a text file in these subfolders. Let’s read in the contents of these text files in each subfolder, store the spam emails’ contents and the ham emails’ contents as two separate data structures, and point our algorithm at each, clearly defining which one is spam and which one is ham.

解压文件

• 我用的是codespace，我想到三种解压方式，一个是vscode也许有extension，另一个是terminal里面使用unzip，还有就是用python来解压，我打算用后两种都尝试一下

• 我直接把这本书的GitHub仓库ekochmar/Getting-Started-with-NLP: This repository accompanies the book “Getting Started with Natural Language Processing” (github.com)在codespace打开，然后建了一个叫learningThrough的文件夹，观察一下目标文件位置，我怕里面的文件直接冲出来于是搞了个subfolder叫test

  然后

  unzip enron1.zip -d ./learningThrough/test
  unzip enron2.zip -d learningThrough/test
  

  这里的路径前面写./ 或者前面不加东西

• 用python来试试

  

  但是遇到了Bad pipe message

  难道是因为我指定的那个try2zip一开始不存在这个directory？

  那我再来一次，直接解压到current directory 下面吧

  import zipfile
  
  # Specify the zip file name
  zip_file = '../enron1.zip'
  
  # Create a ZipFile object
  zip_obj = zipfile.ZipFile(zip_file, 'r')
  
  # Extract all the contents of zip file to the destination folder
  zip_obj.extractall()
  
  # close the Zip File
  zip_obj.close()
  

  import zipfile
  
  # Specify the zip file name
  zip_file = '../enron2.zip'
  
  # Create a ZipFile object
  zip_obj = zipfile.ZipFile(zip_file, 'r')
  
  # Extract all the contents of zip file to the destination folder
  zip_obj.extractall()
  
  # close the Zip File
  zip_obj.close()
  

  好耶

read in the contents of the files

Let’s define a function read_in that will take a folder as an input, read the files in this folder, and store their contents as a Python list data structure.

不得不说这本书给的注释是真的详细…orz

import os
# helps with different text encoding
import codecs
def read_in(folder):
# Using os functionality, list all the files in the specified folder
the files in the specified folder.
    files = os.listdir(folder)
    a_list = []
    # Iterate through the files in the folder
    for a_file in files:
        # Skip hidden files.
        if not a_file.startswith("."):
            # Read the contents of each file.
            f = codecs.open(folder + a_file, "r",encoding="ISO-8859-1",errors="ignore")
            # Add the content of each file to the list data structure.
            a_list.append(f.read())
            # Close the fileafter you readthe contents.
            f.close()
    return a_list

In this code, you rely on Python’s os module functionality to list all the files in the specified folder, and then you iterate through them, skipping hidden files (以.开头的那些文件,such files can be easily identified because their names start with “.” ) that are sometimes automatically created by the operating systems.

Next, you read the contents of each file.

The encoding and errors arguments of codecs.open function will help you avoid errors in reading files that are related to text encoding.

codecs是啥捏

The codecs module in Python provides functions to encode and decode data using various codecs (encoding/decoding algorithms).

Here are some common codecs that you can use with the codecs module:

• utf-8: A Unicode encoding that can handle any character in the Unicode standard. It’s the most widely used encoding for the Web.
• ascii: An encoding for the ASCII character set, which consists of 128 characters.
• latin-1: An encoding for the Latin-1 character set, which consists of 256 characters.
• utf-16: A Unicode encoding that uses two bytes (16 bits) to represent each character.

You add the content of each file to a list data structure, and in the end, you return the list that contains the contents of the files from the specified folder.

verify that the data is uploaded and read in correctly

• 现在我们可以定义spam_list和ham_list—letting the machine know what data represents spam emails and what data represents ham emails.

• Let’s check if the data is uploaded correctly; for example, you can print out the lengths of the lists or check any particular member of the list.

  Summary.txt里面列出来了，那我们就看看条数对不对

  the length of the spam_list should equal the number of spam emails in the enron1/spam/ folder, which should be 1,500, while the length of the ham_list should equal the number of emails in the enron1/ham/, or 3,672. If you get these numbers, your data is uploaded and read in correctly.

  

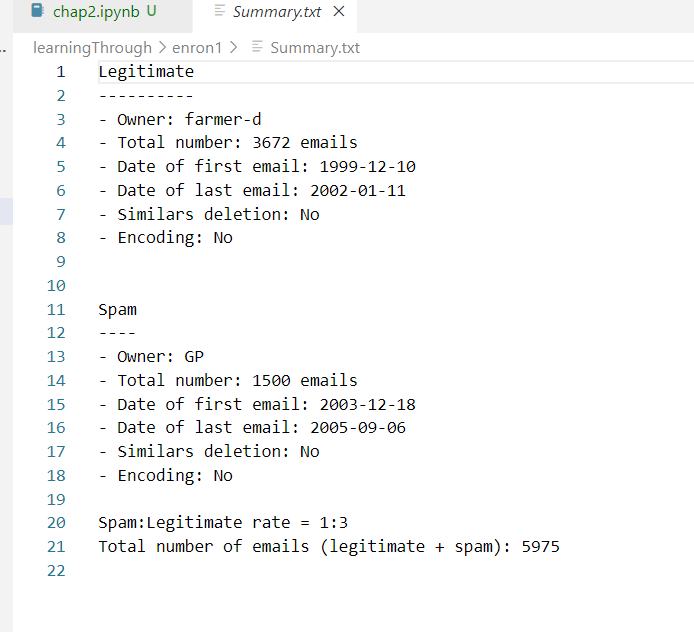
• 代码如下

  spam_list = read_in("./enron1/spam/")
  print(len(spam_list))
  # print(spam_list[0])
  ham_list = read_in("./enron1/ham/")
  print(len(ham_list))
  print(ham_list[0])
  

  条数是对的，好耶

  

combine the data into a single structure

Next, we need to preprocess the data (e.g., by splitting text strings into words) and extract the features. Wouldn’t it be easier if you could run all preprocessing steps over a single data structure rather than over two separate lists?

这里不采用for循环，为了加上标签，我们把每个邮件和其标签组成一个元组，然后再放入一个新的list all_emails 里面

verify一下是否读进去了，输出太长，用切片切一下

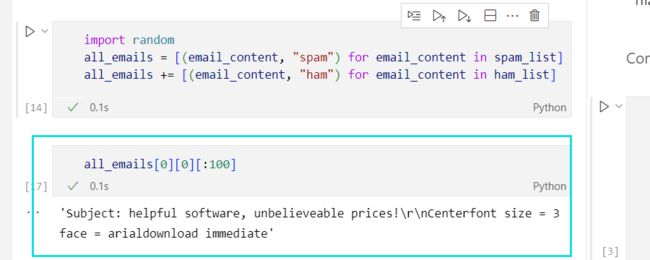
此外，我们还要考虑到划分数据集的随机性

We need to split the data randomly into the training and test sets. To that end（因为那个缘故）, let’s shuffle the resulting list of emails with their labels, and make sure that the shuffle is reproducible by fixing the way in which the data is shuffled. For the shuffle to be reproducible, you need to define the seed for the random operator, which makes sure that all future runs will shuffle the data in exactly the same way.

# Python’s random module will help you shuffle the data randomly.
import random
# Use list comprehensions to create the all_emails list that will keep all emails with their labels.
all_emails = [(email_content, "spam") for email_content in spam_list]
all_emails += [(email_content, "ham") for email_content in ham_list]
# Select the seed of the random operator to make sure that all future runs will shuffle  the data in the same way
random.seed(42)
random.shuffle(all_emails)
# Check the size of the dataset (lengthof the list); it should be equal to 1,500 + 3,672 
# This kind of string is called formatted string literals or f-strings, and it is a new feature introduced in Python 3.6
print (f"Dataset size = {str(len(all_emails))} emails")

Dataset size = 5172 emails

Step 2: Split the text into words

• Remember that the email contents you’ve read in so far each come as a single string of symbols. The first step of text preprocessing involves splitting the running text into words.

• 我们还是用NLTK

  • One of the benefits of this toolkit is that it comes with a thorough documentation and description of its functionality.

    （该工具包的好处是，它具有详尽的文档）

  • NLTK :: nltk.tokenize package

  It takes running text as input and returns a list of words based on a number of customized regular expressions, which help to delimit the text by whitespaces and punctuation marks, keeping common words like U.S.A. unsplit.

run a tokenizer over text

• code

  This code defines a tokenize function that takes a string as input and splits it into words.

  The for-loop within this function appends each identified word from the tokenized string to the output word list; alternatively, you can use list comprehensions(列表生成式) for the same purpose. Finally, given the input, the function prints out a list of words. You can test your intuitions about the words and check your answers to previous exercises by changing the input to any string of your choice

  import nltk
  from nltk import word_tokenize 
  nltk.download('punkt')
  def tokenize(input): 
      word_list = []
      for word in word_tokenize(input):
          word_list.append(word) 
      return word_list
  input = "What's the best way to split a sentence into words?"
  print(tokenize(input))
  

  In addition to the toolkit itself, you need to install NLTK data as explained on www.nltk.org/data.html. Running nltk.download() will install all the data needed for text processing in one go; in addition, individual tools can be installed separately (e.g., nltk.download(‘punkt’) installs NLTK’s sentence tokenizer)

  ['What', "'s", 'the', 'best', 'way', 'to', 'split', 'a', 'sentence', 'into', 'words', '?']
  

  如果我用列表生成式（list comprehension）,那就这样写

  import nltk
  from nltk import word_tokenize 
  def tokenize(input): 
      word_list = [word for word in word_tokenize(input)]
      return word_list
  input = "What's the best way to split a sentence into words?"
  print(tokenize(input))
  

Step 3: Extract and normalize the features

这里作者非常推崇list comprehensions， 确实，我得提高使用它的意识

• Once the words are extracted from running text, you need to convert them into features. In particular, you need to put all words into lowercase to make your algorithm establish the connection between different formats like Lottery and lottery.

• Putting all strings to lowercase can be achieved with Python’s string functionality. To extract the features (words) from the text, you need to iterate through the recognized words and put all words to lowercase. In fact, both tokenization and converting text to lowercase can be achieved using a single line of code with list comprehensions.

  word_list = [word for word in word_tokenize(text.lower())]

  Using list comprehensions, you can combine the two steps—tokenization and converting strings to lowercase—in one line. Here, you first normalize and then tokenize text, but the two steps are interchangeable.

• We define a function get_features that extracts the features from the text of email passed in as input. Next, for each word in the email, you switch on the “flag” that the word is contained in this email by assigning it with a True value. The list data structure all_features keeps tuples containing the dictionary of features matched with the spam or ham label for each email.

Code to extract the features

import nltk
from nltk import word_tokenize

def get_features(text):
    features = {}
    word_list = [word for word in word_tokenize(text.lower())]
    for word in word_list:
    # For each word in the email, switch on the “flag” that this word is contained in the email.
        features[word] = True
    return features
# all_features will keep tuples containing the dictionary of features matched with the label for each email

all_features = [(get_features(email), label) for (email, label) in all_emails]
# Check what features are extracted from an input text
print(get_features("Participate In Our New Lottery NOW!"))
print(len(all_features))
# Check what all_features list data structure contains.

print(len(all_features[0][0]))
print(len(all_features[99][0]))

In the end, the code shows how you can check what features are extracted from an input text and what all_features list data structure contains (e.g., by printing out its length and the number of features detected in the first or any other email in the set)

{'participate': True, 'in': True, 'our': True, 'new': True, 'lottery': True, 'now': True, '!': True}
5172
321
97

随机shuffle确实是有效的，我再来一次得到的是

5172
72
157

其实就是创建了一个dictionary

With this bit of code, you iterate over the emails in your collection (all_emails) and store the features extracted from each email matched with the label. For example, if a spam email consists of a single sentence (e.g., “Participate In Our New Lottery NOW!”), your algorithm will first extract the list of features present in this email and assign a True value to each of them. The dictionary of features will be represented using this format: [‘participate’: True, ‘in’: True, …, ‘now’: True, ‘!’: True]. Then the algorithm will add this data structure to all_features together with the spam label: ([‘participate’: True, ‘in’: True, …, ‘now’: True, ‘!’: True], “spam”)

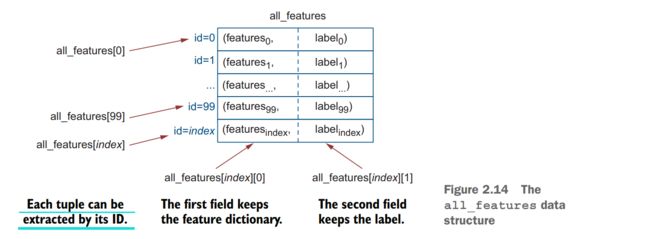
这份代码做了啥，很清晰的解释图！

仔细研究一下上面的数据结构

刚刚那个代码创建了一个list叫all_features, a list of tuples. where each tuple represents an individual email.

So the total length of all_features is equal to the number of emails in your dataset.

As each tuple in this list corresponds to an individual email, you can access each one by the index in the list using all_features[index]: for example, you can access the first email in the dataset as all_features[0] (remember, that Python’s indexing starts with 0), and the hundredth as all_features[99] (for the same reason)

Let’s now clarify what each tuple structure representing an email contains. Tuples pair up two information fields. In this case, a dictionary of features extracted from the email and its label—that is, each tuple in all_features contains a pair (dict_of_ features, label). So if you’d like to access the first email in the list, you call on all_ features[0]; to access its features, you use all_features[0][0]; and to access its label, you use all_features[0][1].

又是一张好图！

For example, if the first email in your collection is a spam email with the content “Participate in our lottery now!”, all_features[0] will return the tuple ([‘participate’: True, ‘in’: True, …, ‘now’: True, ‘!’: True], “spam”); all_features[0][0] will return the dictionary [‘participate’: True, ‘in’: True, …, ‘now’: True, ‘!’: True], and all_features[0][1] will return the value spam

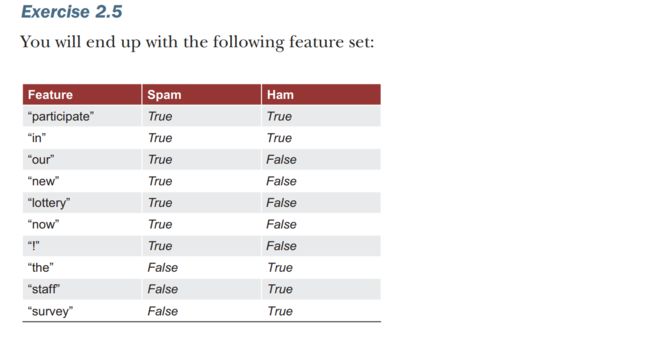
exercise2.5

Imagine your whole dataset contained only one spam email (“Participate In Our New Lottery NOW!”) and one ham email (“Participate in the Staff Survey”). What features will be extracted from this dataset with the code from listing 2.8?(就是上面那个get_feature的代码)

Step 4: Train the classifier

这里作者介绍了用朴素贝叶斯 Naive Bayes来处理

• Next, let’s apply machine learning and teach the machine to distinguish between the features that describe each of the two classes.

• There are several classification algorithms that you can use, and you will come across several of them in this book. But since you are at the beginning of your journey, let’s start with one of the most interpretable（可解释的） ones—an algorithm called Naïve Bayes. Don’t be misled by the word Naïve in its title, though. Despite the relative simplicity of the approach compared to other ones, this algorithm often works well in practice and sets a competitive performance baseline that is hard to beat with more sophisticated（复杂的） approaches. For the spam-filtering algorithm that you are building in this chapter, you will rely on the Naïve Bayes implementation provided with the NLTK library, so don’t worry if some details of the algorithm seem challenging to you. However, if you would like to see what is happening “under the hood,” this section will walk you through the details of the algorithm.

• Naïve Bayes is a probabilistic classifier, which means that it makes the class prediction based on the estimate of which outcome is most likely (i.e., it assesses the probability of an email being spam and compares it with the probability of it being ham), and then selects the outcome that is most probable between the two. In fact, this is quite similar to how humans assess whether an email is spam or ham. When you receive an email that says “Participate in our lottery now! Click on this link,” before clicking on the (potentially harmful) link, you assess how likely it is (i.e., what is the probability?) that it is a ham email and compare it to how likely it is that this email is spam. Based on your experience and all the previous spam and ham emails you have seen before, you might judge that it is much more likely (more probable) that it is a spam email. By the time the machine makes a prediction, it has also accumulated some experience in distinguishing spam from ham that is based on processing a dataset of labeled spam and ham emails.

• In this step, the machine will try to predict whether the email content represents spam or ham. In other words, it will try to predict whether the email is spam or ham given or conditioned on its content. This type of probability, when the outcome (class of spam or ham) depends on the condition (words used as features), is called conditional probability（条件概率）. For spam detection, you estimate P(spam | email content) and P(ham | email content), or generally P(outcome | (given) condition). Then you compare one estimate to another and return the most probable class. For example:

  If P(spam | content) = 0.58 and P(ham | content) = 0.42, predict spam

  If P(spam | content) = 0.37 and P(ham | content) = 0.63, predict ham

  Reminder on the notation(符号): P is used to represent all probabilities; | is used in conditional probabilities, when you are trying to estimate the probability of some event (that is specified before |) given that the condition (that is specified after |) applies.

• In summary, this boils down to(归结为) the following set of actions illustrated in the figure below.

  

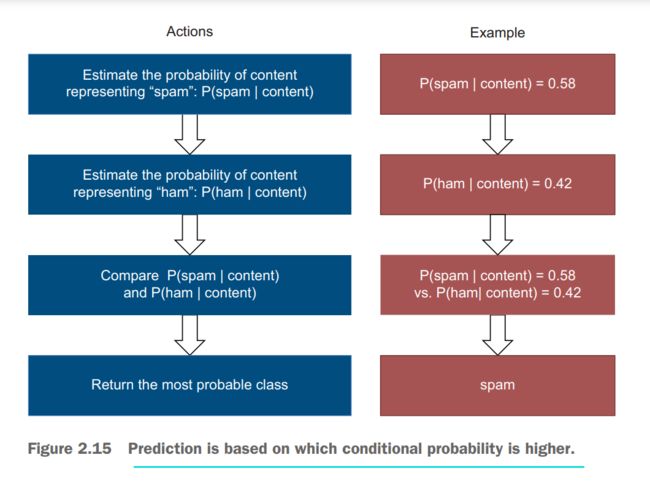
• 我们人往往根据经验有个判断，那么机器呢

  Similarly, a machine can estimate the probability that an email is spam or ham conditioned on its content, taking the number of times it has seen this content leading to a particular outcome:
  $$\begin{gathered} P(spam\mid \text{“Participate in our lottery now!”})=\frac{num(\text{ spam emails with “Participate in our lottery now!”) }}{num(\text{ all emails with “Participate in our lottery now!”) }} \\ P(ham\mid \text{“Participate in our lottery now!”})=\frac{num(\text{ ham emails with “Participate in our lottery now!”) }}{num(\text{ all emails with “Participate in our lottery now!”) }} \end{gathered}$$
  In the general form, this can be expressed as
  $$P(outcome\mid condition)=\frac{\text{ numOfTimes }(\text{ condition led to outcome })}{\text{ numOfTimes }(\text{ condition applied })}$$

• 此时问题出现了

  • You (and the machine) will need to make such estimations for all types of content in your collection, including for the email contents that are much longer than “Participate in our new lottery now!” Do you think you will come across enough examples to reliably make such estimations? In other words, do you think you will see any particular combination of words (that you use as features), no matter how long, multiple times so that you can reliably estimate the probabilities from these examples? The answer is you will probably see “Participate in our new lottery now!” only a few times, and you might see longer combinations of words only once, so such small numbers won’t tell the algorithm much and you won’t be able to use them in the previous expression effectively.
  • Additionally, you will constantly get new emails where the words will be used in a different order and different combinations, so for some of these new combinations you will not have any counts at all, even though you might have counts for individual words in such new emails. The solution to this problem is to split the estimation into smaller bits. For instance, remember that you used tokenization to split long texts into separate words to let the algorithm access the smaller bits of information—words rather than whole sequences. The idea of estimating probabilities based on separate features rather than based on the whole sequence of features (i.e., whole text) is rather similar.

• At the moment, you are trying to predict a single outcome (class of spam or ham) given a single condition that is the whole text of the email; for example, “Participate in our lottery now!” In the previous step, you converted this single text into a set of features as [‘participate’: True, ‘in’: True, …, ‘now’: True, ‘!’: True]. Note that the conditional probabilities like P(spam| “Participate in our lottery now!”) and P(spam| [‘participate’: True, ‘in’: True, …, ‘now’: True, ‘!’: True]) are the same because this set of features encodes the text. Therefore, if the chances of seeing “Participate in our lottery now!” are low, the chances of seeing the set of features [‘participate’: True, ‘in’: True, …, ‘now’: True, ‘!’: True] encoding this text are equally low.

  Is there a way to split this set to get at more fine-grained（细粒度）, individual probabilities, such as to establish a link between [‘lottery’: True] and the class of spam?

  • Unfortunately, there is no way to split the conditional probability estimation like P(outcome | conditions) when there are multiple conditions specified; however, it is possible to split the probability estimation like P(outcomes | condition) when there is a single condition and multiple outcomes. In spam detection, the class is a single value (it is spam or ham), while features are a set ([‘participate’: True, ‘in’: True, …, ‘now’: True, ‘!’: True]). If you can flip（浏览） around the single value of class and the set of features in such a way that the class becomes the new condition and the features become the new outcomes, you can split the probability into smaller components and establish the link between individual features like [‘lottery’: True] and class values like spam.

    

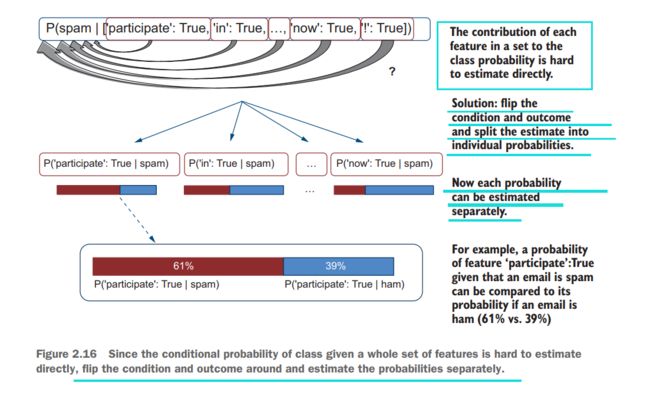
下面要学习公式推导咯

• Luckily, there is a way to flip the outcomes (class) and conditions (features extracted from the content) around! Let’s look into the estimation of conditional probabilities again: you estimate the probability that the email is spam given that its content is “Participate in our new lottery now!” based on how often in the past an email with such content was spam. For that, you take the proportion of the times you have seen “Participate in our new lottery now!” in a spam email among the emails with this content. You can express it as
  $$\begin{gathered} P(spam\mid \text{“Participate in our lottery now!”})= \\ \frac{\mathrm{P}\text{ (“Participate in our lottery now!” is in a spam email })}{P\text{ (“Participate in our lottery now!” is used in an email) }} \end{gathered}$$
  Let’s call this Formula 1. What is the conditional probability of the content “Participate in our new lottery now!” given class spam, then? Similarly the probabilities earlier, you need the proportion of times you have seen “Participate in our new lottery now!” in a spam email among all spam emails. You can express it as
  $$P(\text{“Participate in our lottery now!”}\mid spam)=\frac{\mathrm{P}\text{ (“Participate in our lottery now!" is in a spam email) }}{P(\text{ an email is spam) }}$$
  Let’s call this Formula 2. Every time you use conditional probabilities, you need to divide how likely it is that you see the condition and outcome together by how likely it is that you see the condition on its own—this is the bit（约束）after |. Now you can see that both Formulas 1 and 2 rely on how often you see particular content in an email from a particular class. They share this bit, so you can use it to connect the two formulas. For instance, from Formula 2 you know that
  $$\begin{gathered} \mathrm{P}\text{ (“Participate in our lottery now!" is in a spam email) }= \\ P(\text{“Participate in our lottery now!”}\mid spam)\times P(\text{ an email is spam) } \end{gathered}$$
  Now you can fit this into Formula 1：
  $$\begin{gathered} P(spam\mid \text{“Participate in our lottery now!”})= \\ \frac{\mathrm{P}\text{ (“Participate in our lottery now!” is in a spam email })}{P\text{ (“Participate in our lottery now!” is used in an email) }}= \\ \frac{P(\text{“Participate in our lottery now!”}\mid spam)\times P(\text{ an email is spam) }}{P\text{ (“Participate in our lottery now!” is used in an email) }} \end{gathered}$$
  图解如下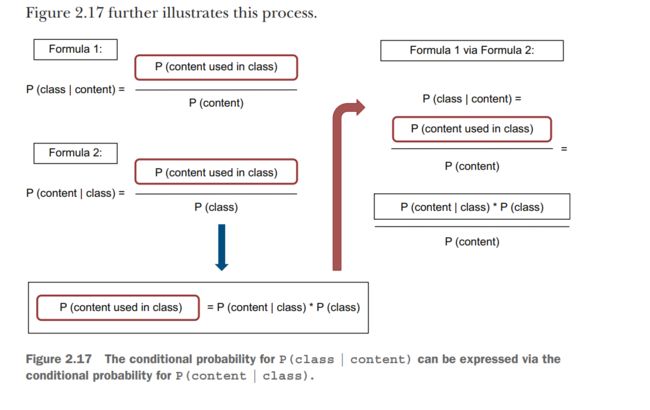

  

• 总结一下

  

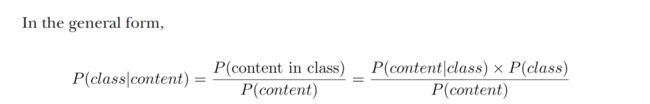
  • In other words, you can express the probability of a class given email content via the probability of the content given the class. Let’s look into these two new probabilities, P(content | class) and P(class), more closely as they have interesting properties:
    • P(class) expresses the probability of each class. This is simply the distribution of the classes in your data. Imagine opening your inbox and seeing a new incoming email. What do you expect this email to be—spam or ham? If you mostly get normal emails and your spam filter is working well, you will probably expect a new email to also be ham rather than spam. For example, the enron1/ ham folder contains 3,672 emails, and the spam folder contains 1,500 emails, making the distribution approximately 71:29, or P(“ham”)=0.71 and P(“spam”)=0.29. This is often referred to as prior probability, as it reflects the beliefs of the classifier about where the data comes from prior to any particular evidence; for example, here the classifier will expect that it is much more likely (chances are 71:29) that a random incoming email is ham.
    • P(content | class) is the evidence, as it expresses how likely it is that you (or the algorithm) will see this particular content given that the email is spam or ham. For example, imagine you have opened this new email and now you can assess how likely it is that these words are used in a spam email versus（与） how likely it is that they are used in a ham email. The combination of these factors may in the end change your, or the classifier’s, original belief about the most likely class that you had before seeing the content (evidence).

• Now you can replace the conditional probability of P(class | content) with P(content | class); for example, whereas before you had to calculate P("spam" | “Participate in our new lottery now!”) or equally P("spam" | ['participate': True, 'in': True, ..., 'now': True, '!': True]), which is hard to do because you will often end up with too few examples of exactly the same email content or exactly the same combination of features, now you can estimate P(['participate': True, 'in': True, ..., 'now': True, '!': True] | "spam")instead. But how does this solve the problem? Aren’t you still dealing with a long sequence of features?

  这时候朴素贝叶斯又派上用场辣

  Here is where the “naïve” assumption in Naïve Bayes helps: it assumes that the features are independent of each other, or that your chances of seeing a word lottery in an email are independent of seeing a word new or any other word in this email before. Therefore, you can estimate the probability of the whole sequence of features given a class as a product of probabilities of each feature given this class:
  $$\begin{array}{c}\\ P([\text{ ’participate’: True, ’in’: True, }\dots ,\text{ ’now’: True, ’!’: True }]\text{ "spam" })=\\ \\ P(\text{ ’participate’: True }\mid \text{ "spam") }\times P(\text{ ’in’: True }\mid \text{ "spam" })\times \dots \times P(\text{ ’!" : True }\mid \text{ "spam") }\end{array}$$
  If you express ['participate': True] as the first feature in the feature list, or $f_1,{[}^{\prime }i{n}^{\prime }:True]$ as$ f_{2}$, and so on, until $f_n={[}^{\prime }{!}^{\prime }:True]$, you can use the general formula
  $$P\left(\left[f_1,f_2,\dots ,f_n\right]\mid \text{ class }\right)=P\left(f_1\mid \text{ class }\right)\times P\left(f_2\mid \text{ class }\right)\times \dots \times P\left(f_n\mid \text{ class }\right)$$

• Now that you have broken down the probability of the whole feature set given class into the probabilities for each word given that class, how do you actually estimate them? Since for each email you note which words occur in it, the total number of times you can switch on the flag ['feature': True] equals the total number of emails in that class, while the actual number of times you switch on this flag is the number of emails where this feature is actually present. The conditional probability P(feature | class) is simply the proportion:
  KaTeX parse error: Expected 'EOF', got '_' at position 108: …}{\text { total_̲num(emails in c…

• Now you have all the components in place. Let’s iterate through the classification steps again.

  • First, during the training phase, the algorithm learns prior class probabilities. This is simply class distribution—for example, P(ham)=0.71 and P(spam)=0.29.

  • Secondly, the algorithm learns probabilities for each feature given each of the classes. This is the proportion of emails with each feature in each class—for example, P('meeting':True | ham) = 0.50. During the test phase, or when the algorithm is applied to a new email and is asked to predict its class, the following comparison from the beginning of this section is applied
    $$\{\begin{array}{ll}P(\text{ spam }\mid \text{ content })\ge P(\text{ ham }\mid \text{ content })& \Rightarrow \text{ spam }\\ \text{ otherwise }& \Rightarrow \text{ ham }\end{array}$$
    This is what we started with originally, but we said that the conditions are flipped, so it becomes
    $$\{\begin{array}{ll}\frac{P(\text{ content }\mid \text{ spam })\times P(\text{ spam })}{P(\text{ content })}\ge \frac{P(\text{ content }\mid \text{ ham })\times P(\text{ ham })}{P(\text{ content })}& \Rightarrow \text{ spam }\\ \text{ otherwise }& \Rightarrow \text{ ham }\end{array}$$
    Note that we end up with P(content) in the denominator(分母) on both sides of the expression, so the absolute value of this probability doesn’t matter, and it can be removed from the expression altogether. As an aside（顺便说一句）, since the probability always has a positive value, it won’t change the comparative values on the two sides; for example, if you were comparing 10 to 4, you would get 10 > 4 whether you divide the two sides by the same positive number like (10/2) > (4/2) or not. So we can simplify the expression as
    $$\{\begin{array}{ll}P(\text{ content }\mid \text{ spam })\times P(\text{ spam })\ge P(\text{ content }\mid \text{ ham })\times P(\text{ ham })& \Rightarrow \text{ spam }\\ \text{ otherwise }& \Rightarrow \text{ ham }\end{array}$$
    P(spam) and P(ham) are class probabilities estimated during training, and P(content | class), using naïve independence assumption, are products(乘积) of probabilities, so
    $$\{\begin{array}{ll}& \\ P\left(\left[f_1,f_2,\dots ,f_n\right]\mid \text{ spam }\right)\times P(\text{ spam })\ge P\left(\left[f_1,f_2,\dots ,f_n\right]\mid ham\right)\times P(\text{ ham })& \Rightarrow \text{ spam }\\ & \\ \text{ otherwise }& \Rightarrow \text{ ham }\end{array}$$
    is split into the individual feature probabilities as
    $$\{\begin{array}{ll}& \\ P\left(f_1\mid \text{ spam }\right)\times \dots \times P\left(f_n\mid \text{ spam }\right)\times P(\text{ spam })\ge P\left(f_1\mid \text{ ham }\right)\times \dots \times P\left(f_n\mid \text{ ham }\right)\times P(\text{ ham })& \Rightarrow \text{ spam }\\ & \\ \text{ otherwise }& \Rightarrow \text{ ham }\end{array}$$
    图解，又是好图~

    

Code to train a Naïve Bayes classifier

• NLTK有朴素贝叶斯的封装可以直接用

from nltk import NaiveBayesClassifier, classify

def train(features, propotion):
    train_size = int(len(features) * propotion)
    #initialize the training and testing sets
    train_set, test_set = features[:train_size], features[train_size:]
    print(f"Training set size: {str(len(train_set))} emails")
    print(f"Test set size: {str(len(test_set))} emails")
    #train the classifier
    classifier = NaiveBayesClassifier.train(train_set)
    return train_set, test_set, classifier
#Apply the train function using 80% (or a similar proportion) of emails for training
train_set, test_set, classifier = train(all_features, 0.8)

Exercise 2.6

Suppose you have five spam emails and ten ham emails. What are the conditional probabilities for P('prescription':True | spam), P('meeting':True | ham), P('stock':True | spam), and P('stock':True | ham), if

• Two spam emails contain the word prescription?
• One spam email contains the word stock?
• Three ham emails contain the word stock?
• Five ham emails contain the word meeting?

Step 5: Evaluate your classifier

• Finally, let’s evaluate how well the classifier performs in detecting whether an email is spam or ham. For that, let’s use the accuracy score returned by the NLTK’s classifier. In addition, the NLTK’s classifier allows you to inspect the most informative features (words). For that, you need to specify the number of the top most informative features to look into (e.g., 50 here).

• code

  def evaluate(train_set, test_set,classifier):
      # chech how the classfiier performs on the training and test sets
      print(f"Accuracy on the training set: {str(classify.accuracy(classifier, train_set))}")
      print(f"Accuracy of the test set: {str(classify.accuracy(classifier, test_set))}")
      # check which words are most informative for the classifier
      classifier.show_most_informative_features(50)
  evaluate(train_set, test_set, classifier)
  

  

  the most informative features—that is, the list of words that are most strongly associated with a particular class. This is functionality of the classifier that is implemented in NLTK, so all you need to do is call on this function as classifier.show_most_informative_features and specify the number of words nthat you want to see as an argument. This function then returns the top n words ordered by their “informativeness” or predictive power. Behind the scenes, the function measures “informativeness” as the highest value of the difference in probabilities between P(feature | spam) and P(feature | ham)— that is, max[P(word: True | ham) / P(word: True | spam)] for most predictive ham features, and max[P(word: True | spam) / P(word: True | ham)] for most predictive spam features (check out NLTK’s documentation for more information: https://www.nltk.org/api/nltk.classify.naivebayes.html). The output shows that such words (features) as prescription(处方), pain, health, and so on are much more strongly associated with spam emails. The ratios on the right show the comparative probabilities for the two classes: for instance, P("prescription" | spam) is 130.9 times higher than P("prescription" | ham). On the other hand, nomination is more strongly associated with ham emails. As you can see, many spam emails in this dataset are related to medications, which shows a particular bias; the most typical spam that you personally get might be on a different topic altogether.

  One other piece of information presented in this output is accuracy. Test accuracy shows the proportion of test emails that are correctly classified by Naïve Bayes among all test emails. The preceding(前面的) code measures the accuracy on both the training data and test data. Note that since the classifier is trained on the training data, it actually gets to “see” all the correct labels for the training examples. Shouldn’t it then know the correct answers and perform at 100% accuracy on the training data? Well, the point here is that the classifier doesn’t just retrieve（挽回） the correct answers; during training, it has built some probabilistic model (i.e., learned about the distribution of classes and the probability of different features), and then it applies this model to the data. So, it is actually very likely that the probabilistic model doesn’t capture all the things in the data 100% correctly. For example, there might be noise and inconsistencies in the real emails. Note that “2004” gets strongly associated with the spam emails and “2001” with the ham emails, although it does not mean that there is anything peculiar（奇怪的） about the spam originating from 2004. This might simply show a bias in the particular dataset, and such phenomena are hard to filter out in any real data, especially when you rely on the data collected by other researchers. This means that if some ham email in training data contains “2004” and a variety of other words that are otherwise related to spam, this email might get misclassified as spam by the algorithm. Similarly, as many medication-related words are strongly associated with spam, a rare ham email that is actually talking about some medication the user ordered might get misclassified as spam.

  这里的训练集测试集的accuracy都不错，说明泛化能力还可以

Code to check the contexts of specific words

If you’d like to gain any further insight into how the words are used in the emails from different classes, you can also check the occurrences of any particular word in all available contexts. For example, the word stocks features as a very strong predictor of spam messages. Why is that? You might be thinking, Okay, some emails containing “stocks” will be spam, but surely there must be contexts where “stocks” is used in a completely legitimate way?

from nltk.text import Text

def concordance(data_list, search_word):
    for email in data_list:
        word_list = [word for word in word_tokenize(email.lower())]
        text_list = Text(word_list)
        if search_word in word_list:
            text_list.concordance(search_word)
print ("STOCKS in HAM:")
concordance(ham_list, "stocks")
print ("\n\nSTOCKS in SPAM:")
concordance(spam_list, "stocks")

This code shows how you can use NLTK’s concordancer(语料库检索工具), a tool that checks for the occurrences of the specified word and prints out this word in its contexts. By default, NLTK’s concordancer prints out the search_word surrounded by the previous 36 and the following 36 characters, so note that it doesn’t always result in full words. Once the use of concordancer is defined in the function concordance, you can apply it to both ham_list and spam_list to find the different contexts of the word stocks.

2.4 Deploying your spam filter in practice

apply spam filtering to new emails

test_spam_list = ["Participate in our new lottery!", "Try out this new medicine"]
test_ham_list = ["See the minutes from the last meeting attached", 
                 "Investors are coming to our office on Monday"]

test_emails = [(email_content, "spam") for email_content in test_spam_list]
test_emails += [(email_content, "ham") for email_content in test_ham_list]

new_test_set = [(get_features(email), label) for (email, label) in test_emails]

evaluate(train_set, new_test_set, classifier)

print out the predicted label

for email in test_spam_list:
    print (email)
    print (classifier.classify(get_features(email)))
for email in test_ham_list:
    print (email)
    print (classifier.classify(get_features(email)))

Participate in our new lottery!
spam
Try out this new medicine
spam
See the minutes from the last meeting attached
ham
Investors are coming to our office on Monday
ham

classify the emails read in from the keyboard

while True:
    email = input("Type in your email here (or press 'Enter'): ")
    if len(email)==0:
        break
    else: 
        prediction = classifier.classify(get_features(email))
        print (f"This email is likely {prediction}\n")

这还挺好玩的~

感觉这本书的逻辑很清晰，而且很详细，很多地方真的是手把手step-by-step的讲解了

Summary

• Classification is concerned with assigning objects to a predefined set of categories, groups, or classes based on their characteristic properties. There is a whole family of NLP and machine-learning tasks that deal with classification.
• Humans perform classification on a regular basis, and machine-learning algorithms can be taught to do that if provided with a sufficient number of examples and some guidance from humans. When the labeled examples and the general outline of the task are provided for the machine, this is called supervised learning.
• Spam filtering is an example of a binary classification task. The machine has to learn to distinguish between exactly two classes—spam and normal email (often called ham).
• Classification relies on specific properties of the classified objects. In machine learning terms, such properties are called features. For spam filtering, some of the most informative features are words used in the emails.
• To build a spam-filtering algorithm, you can use one of the publicly available spam datasets. One such dataset is the Enron spam dataset.
• A classifier can be built in five steps: (1) reading emails and defining classes, (2) extracting content, (3) converting the content into features, (4) training an algorithm on the training set, and (5) evaluating it on the test set.
• The data comes in as a single string of symbols. To extract the words from it, you may rely on the NLP tools called tokenizers (or use regular expressions to implement one yourself).
• NLP libraries, such as the Natural Language Processing Toolkit (NLTK), come with such tools, as well as implementations of a range of frequently used classifiers.
• There are several machine-learning classifiers, and one of the most interpretable among them is Naïve Bayes. This is a probabilistic classifier. It assumes that the data in two classes is generated by different probability distributions, which are learned from the training data. Despite its simplicity and “naïve” feature independence assumption, Naïve Bayes often performs well in practice and sets a competitive baseline for other more sophisticated algorithms.
• It is important that you split your data into training sets (e.g., 80% of the original dataset) and test sets (the rest of the data), and train the classifier on the training data only so that you can assess it on the test set in a fair way. The test set serves as new unseen data for the algorithm, so you can come to a realistic conclusion about how your classifier may perform in practice.
  Processing Toolkit (NLTK), come with such tools, as well as implementations of a range of frequently used classifiers.
• There are several machine-learning classifiers, and one of the most interpretable among them is Naïve Bayes. This is a probabilistic classifier. It assumes that the data in two classes is generated by different probability distributions, which are learned from the training data. Despite its simplicity and “naïve” feature independence assumption, Naïve Bayes often performs well in practice and sets a competitive baseline for other more sophisticated algorithms.
• It is important that you split your data into training sets (e.g., 80% of the original dataset) and test sets (the rest of the data), and train the classifier on the training data only so that you can assess it on the test set in a fair way. The test set serves as new unseen data for the algorithm, so you can come to a realistic conclusion about how your classifier may perform in practice.
• Once satisfied with the performance of your classifier on the test data, you can deploy（部署，利用） it in practice.