【强化学习】 Q-Learning

• 【强化学习】相关基本概念
• 【强化学习】 Q-Learning
• 【强化学习】 Q-Learning 案例分析
• 【强化学习】 Sarsa
• 【强化学习】 Sarsa（lambda）

---

Q-Learning

强化学习的过程是智能体从与环境的交互中不断学习以完成特定目标

Q-Learning是强化学习的主要算法之一，是一种记录行为值 (Q value) 的方法

• Q-Learning基于的一个关键假设是智能体和环境的交互可看作为一个马尔可夫决策过程(MDP)，即智能体当前所处的状态和所选择的动作，决定一个固定的状态转移概率分布、下一个状态、并得到一个即时回报。Q-Learning的目标是寻找一个策略可以最大化将来获得的报酬。
• Q--Learning中，Q即为Q(s,a)，每个Q(s,a)对应一个相应的Q值，就是在某一时刻的 s 状态下(s∈S)，采取a (a∈A)动作能够获得收益的期望，环境会根据agent的动作反馈相应的回报reward (r)，所以算法的主要思想就是将State与Action构建成一张Q-table来存储Q值，然后根据Q值来选取能够获得最大的收益的动作。

---

算法流程

Q-Learning算法的核心是用一张Q-table来存储关于状态s与行为a的期望值Q(s,a)，因此这张表是算法的关键

那如何获得能够反映出在真实状态s下进行行为a所获得的期望值呢？

（1）构建预估table：假设我们处于状态s1，行为准则有两种a1和a2，那我们可以构建一个关于s1与a1、a2的表如下：

	a1	a2
s1	-2	1

表格里的数据，即Q(s1,a1)= -2 与 Q(s1,a2)=1 是我们预估值

（2）选择行为：对于两种行为的期望预估值，我们选择较大的，即a2，因此我们更新个体状态为s2，同时环境对于(s1,a2)将反馈给我们实际的奖励r1

（3）继续构建table：此时个体处于s2状态，行为有a1和a2，因此我们可以以预估值继续构建table：

	a1	a2
s1	-2	1
s2	-4	2

（4）计算Q的现实值：在新的tabel中，我们继续选择较大的期望预估值，即a2，因此我们可以得到Q(s1,a2)的现实值与估计值：

• Q(s1,a2)现实值：
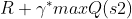
• Q(s1,a2)估计值：Q(s1,a2)=1 (最早建立的table中)
• 其中 Q(s2)就是我们对下一个状态s2的估计的Q值，即Q(s2,a1)、Q(s2,a2)，这两个Q还没有发生，因此也是我们估计的s2状态在a1和a2行为下的反馈

其中R可以表示前面所有的行为下环境反馈的真实值的总和，对于该例子中，R=r1

（5）更新Q-table里的Q(s1,a2)：

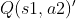• 为老的Q值，即Q估计
• 为新的Q值
• d为Q的现实值与估计值的差，差距d=现实-估计
•   为学习效率
• 可以理解为：新的Q=Q估计+ α * (Q现实-Q估计)

由于目前S2状态还没有做出实际行为，因此还没发更新Q(s2,a2)，需要等s2做出选择得到实际的奖励之后，按章上述方法更新Q-table

总结以上，Q-learning的算法如下：

• 每次更新都用到Q现实与Q估计，同时这一步Q(s1,a2)的现实中，包含了下一步Q(s2)的估计
• 对下一步衰减的最大估计与这一步的奖励作为这一步的现实
• ε-greedy 是一种行为决策策略，如ε=0.9，说明90%按照Q-table的最优值来决策行为，10%采用随机选择来决策行为
• α 是学习效率，来决定这次误差有多少需要学习，值小于1
•  γ 是衰减值，对未来奖励的衰减

总结以上可以得到：

...

...

可以看出Q(s1)是后面所有行为的奖励，但是这些奖励在逐渐衰减

γ=1时可以获得后面全部步骤的所有价值的奖励

γ=0时只能获得眼前的奖励

γ=0~1，不只着眼于眼前的奖励，逐渐可以获得后续步骤的奖励

---

简单案例

一个简单的案例：o为智能体，起始位置在最左边，目的位置为离T最近的位置，行为可以有向左、向右。让o学习可以从起始位置到达最终位置

这个案例中需要有一下几个部分：

• 建立初始化Q-table
• 动作行为的选择
• 环境的建立
• 环境的反馈

（1）初始化全局变量以及需要的库

import numpy as np
import pandas as pd
import time

np.random.seed(2)  # 产生一组伪随机数列（每次运行随机过程一样）

# 一组全局变量
N_STATES = 6  # 多少种状态
ACTION = ['left', 'right']  # 两种可选行为
EPSILON = 0.9  # 贪婪参数：90%选择最优动作，10%选择随机动作
ALPHA = 0.1  # 学习效率
LAMBDA = 0.9  # 衰减度r
MAX_EPISODES = 13  # 最大回合数
FRESH_TIME = 0.1  # 走一步花费的时间

（2）建立初始化Q-table

初始建立的Q-table(S状态, A行为)赋值为零，6种状态，2种行为

# 建立初始化Q-table
def build_q_table(n_states, actions):
    table = pd.DataFrame(
        np.zeros((n_states, len(actions))),  # 全零初始化
        columns=actions,
    )
    return table

（3）动作行为的选择

• ε=0.9
• 如果随机数大于0.9或者刚开始table全为0时，则随机选择行为
• 如果随机数小于0.9则选择table里期望值最大的行为

# 选动作
def choose_action(state, q_table):
    state_action = q_table.iloc[state, :]
    if (np.random.uniform() > EPSILON) or (state_action.all() == 0):  # 判断，如果大于90% 随机选择；如果小于则选择state_action里较大的
        action_name = np.random.choice(ACTION)
    else:
        action_name = state_action.idxmax()
    return action_name

（4）环境的建立

# 建立环境
def update_env(S, episode, step_counter):
    env_list = ['-'] * (N_STATES - 1) + ['T']
    if S == 'terminal':
        interaction = 'Episode %s:total_steps = %s' % (episode+1,step_counter)
        print('\r{}'.format(interaction), end='')
        time.sleep(2)
        print('\r                     ', end='')
    else:
        env_list[S] = 'o'
        interaction = ''.join(env_list)
        print('\r{}'.format(interaction), end='')
        time.sleep(FRESH_TIME)

（5）环境的反馈

• 若向右，同时位置状态为4，即其实位置向右移动4步则离T最近为最终位置，此时到达终点，奖励为1，S=terminal
• 若向右，位置状态不为4，则S+1
• 若向左，则奖励R为0，同时S为零时，说明在起始位置，所以S不变，其他情况S-1

# 环境和环境的反馈
def get_env_feedback(S, A):
    if A == 'right':
        if S == N_STATES - 2:
            S_ = 'terminal'
            R = 1
        else:
            S_ = S + 1
            R = 0
    else:
        R = 0
        if S == 0:
            S_ = S
        else:
            S_ = S - 1
    return S_, R

（6）主循环

# 主循环
def rl():
    q_table = build_q_table(N_STATES, ACTION)
    for episode in range(MAX_EPISODES):
        step_counter = 0
        S = 0  # 初始位置：最左边
        is_terminated = False  # 初始不是终止
        update_env(S, episode, step_counter)  # 更新环境
        while not is_terminated:

            A = choose_action(S, q_table)  # 初始位置选择行为
            S_, R = get_env_feedback(S, A)  # 得到下一个行为的奖励
            q_predict = q_table.loc[S, A]  # 估计值
            if S_ != 'terminal':
                q_target = R + LAMBDA * q_table.iloc[S_, :].max()  # 真实值
            else:
                q_target = R  # 回合终止，没有衰减 等于R
                is_terminated = True  # 已经终止

            q_table.loc[S, A] += ALPHA * (q_target - q_predict)  # 更行Q值
            S = S_  # 更新下一步的状态
            update_env(S, episode, step_counter + 1)  # 更新下一步环境
            step_counter += 1
    return q_table

（7）执行

if __name__ == "__main__":
    q_table = rl()
    print('\r\nQ-table:\n')
    print(q_table)

最后的效果就是o刚开始左右探索，需要很多步骤才可以到T，训练一会儿之后，就可以很快直接到T位置

Q-table的变化：

• 数字代表每次达到最终目标的回合数，可以看到刚开始比较多，后期很快就能达到目标
• 最优目标的回合数为5次，而后面仍然有6次或7次，这也就是设定的ε=0.9种有10% 的机会不选择最优行为，而是随机行为导致的
• Q-table可以看到最开始设定为全0，后面每个回合都通过学习率α =0.1以及衰减率γ=0.9，将后续行为中学习到的行为带来的奖励记录更新在Q-table中。
• 最终获得的Q-table将是自我学习之后获得的​

如果想继续深入学习更复杂点的Q-Learning案例，可以跳转【强化学习】Q-Learning 案例分析

 

代码以及学习过程来源：莫烦Python教学（十分感谢莫烦大佬的教学视频）