深度学习课程项目

多元线性回归的随机梯度方法

代码

import numpy as np
w=np.array([5,3,4]).transpose()
b=np.array([100])
def compute_error_for_given_points(b,w,points):
    totalError = 0
    for i in range(0, len(points)):
        x = points[i].x
        y = points[i].y
        totalError += (y-(np.dot(w,x)+b)) ** 2
    return totalError / float(len(points))
def step_gradient(b_current, w_current, points, learningRate):
    b_gradient = 0
    w_gradient = np.zeros((len(w_current)))
    N = float(len(points))
    for i in range(0, len(points)):
        x = points[i].x
        y = points[i].y
        residual = np.dot(w_current,x)+b_current - y
        b_gradient += (2) * residual
        w_gradient += (2/N) * residual * x
    new_b = b_current - (learningRate * b_gradient)
    new_w = w_current - (learningRate * w_gradient)
    return [new_b, new_w]
def gradient_descent_runner(starting_b, starting_w, points, learning_rate, num_iterations):
    b = starting_b
    w = starting_w
    percent_old = 0
    for i in range(num_iterations):
        percent = i/num_iterations
        if percent-percent_old > 0.01:
            percent_old = percent
            print("\r进度为{:.2f}%".format(percent*100), end="")
        b, w = step_gradient(b, w, points, learning_rate)
    print("\n")
    return [b, w]
class Point:
    def __init__(self, x, y):
        self.x = x
        self.y = y
x = np.random.random((1000,3))*10+10
y = b + np.matmul(x,w) + np.random.normal(0, 1, 1000)
# points = tf.data.Dataset.from_tensor_slices((x,y))
points = np.ndarray((1000), dtype=Point)
for i in range(1000):
    points[i] = Point(x[i], y[i])
loss = compute_error_for_line_given_points(0, np.array([0,0,0]), points)
print(f"loss before: {loss}")
b, w = gradient_descent_runner(0, np.array([0,0,0]), points, 0.0001, 5000)
loss = compute_error_for_line_given_points(b, w, points)
print(f"loss after: {loss}")
print(f"{b} + {w}*x")

效果

原理

实值函数线性模型

$损失函数为MSE时，L(\mathbf{w})=\frac{1}{n}{\Sigma }_{i=1}^n(\hat{f}({\mathbf{x}}^{(i)})-y^{(i)}{)}^2。当模型为\hat{f}(\mathbf{x})=\hat{y}=b+{\Sigma }_{i=1}^d{w}_i{x}_i时，\frac{\partial L(\mathbf{w})}{\partial b}=\frac{2}{n}{\Sigma }_{i=1}^n({\hat{y}}^{(i)}-y^{(i)}),\frac{\partial L(\mathbf{w})}{\partial w_j}=\frac{2}{n}{\Sigma }_{i=1}^n({\hat{y}}^{(i)}-y^{(i)})x_j^{(i)}。由对向量求导的定义得：\frac{\partial L(\mathbf{w})}{\partial \mathbf{w}}=\frac{2}{n}{\Sigma }_{i=1}^n({\hat{y}}^{(i)}-y^{(i)}){\mathbf{x}}^{(i)}。将b视为w_0的增广形式结果类似，只需x_0固定为1.$

实值函数线性基函数模型 linear basis function model

$当模型为\hat{f}(\mathbf{x})=\hat{y}={\Sigma }_{i=0}^m{w}_i{\varphi }_i(\mathbf{x})时,$
$其中{\varphi }_i(\mathbf{x})为d元实值函数，可退化为Polynomial:x_i^i,Gussian:e^{\frac{(x_i-{\mu }_i{)}^2}{2{\sigma }_i^2}},Sigmoidal:\frac{1}{1+e^{\frac{x_i-{\mu }_i}{{\sigma }_i}}}.并保持{\varphi }_0(\mathbf{x})\equiv 1$
$上述求导结果变为\frac{\partial L(\mathbf{w})}{\partial \mathbf{w}}=\frac{2}{n}{\Sigma }_{i=1}^n({\hat{y}}^{(i)}-y^{(i)})\mathbf{\varphi }({\mathbf{x}}^{(i)})$

实值函数线性基函数模型求导的矩阵形式解 derivation

$在求解\frac{\partial L(\mathbf{w})}{\partial \mathbf{w}}=0时需要将上式中的\mathbf{w}分离.即对n个向量求和为0向量问题需转化为矩阵问题$
${\Sigma }_{i=1}^n({\hat{y}}^{(i)}-y^{(i)})\mathbf{\varphi }({\mathbf{x}}^{(i)})$
$={\Sigma }_{i=1}^n\mathbf{\varphi }({\mathbf{x}}^{(i)})({\hat{y}}^{(i)}-y^{(i)})$
$=(\mathbf{\varphi }({\mathbf{x}}^{(1)}),\mathbf{\varphi }({\mathbf{x}}^{(2)},)\cdots ,\mathbf{\varphi }({\mathbf{x}}^{(n)})\cdot ({\hat{y}}^{(1)}-y^{(1)},{\hat{y}}^{(2)}-y^{(2)},\cdots ,{\hat{y}}^{(n)}-y^{(n)}{)}^{\prime }$
= ( ϕ ( x ( 1 ) ) , ϕ ( x ( 2 ) ) , ⋯   , ϕ ( x ( n ) ) ⋅ ( w ′ ϕ ( x ( 1 ) ) − y ( 1 ) , w ′ ϕ ( x ( 2 ) ) − y ( 2 ) , ⋯   , w ′ ϕ ( x ( n ) ) − y ( n ) ) =(\boldsymbol \phi(\boldsymbol x^{(1)}),\boldsymbol \phi(\boldsymbol x^{(2)}),\cdots,\boldsymbol \phi(\boldsymbol x^{(n)})\cdot \left( %左括号 \begin{array}{c} %该矩阵一共3列，每一列都居中放置 \boldsymbol w' \boldsymbol \phi(\boldsymbol x^{(1)})- y^{(1)},\\ \boldsymbol w' \boldsymbol \phi(\boldsymbol x^{(2)})- y^{(2)},\\ \cdots,\\ \boldsymbol w' \boldsymbol \phi(\boldsymbol x^{(n)})- y^{(n)} \end{array} \right) =(ϕ(x(1)),ϕ(x(2)),⋯,ϕ(x(n))⋅ ​w′ϕ(x(1))−y(1),w′ϕ(x(2))−y(2),⋯,w′ϕ(x(n))−y(n)​ ​
= ( ϕ ( x ( 1 ) ) , ϕ ( x ( 2 ) ) , ⋯   , ϕ ( x ( n ) ) ⋅ ( ϕ ( x ( 1 ) ) ′ w − y ( 1 ) , ϕ ( x ( 2 ) ) ′ w − y ( 2 ) , ⋯   , ϕ ( x ( n ) ) ′ w − y ( n ) ) =(\boldsymbol \phi(\boldsymbol x^{(1)}),\boldsymbol \phi(\boldsymbol x^{(2)}),\cdots,\boldsymbol \phi(\boldsymbol x^{(n)})\cdot \left( %左括号 \begin{array}{c} %该矩阵一共3列，每一列都居中放置 \boldsymbol \phi(\boldsymbol x^{(1)})'\boldsymbol w- y^{(1)},\\ \boldsymbol \phi(\boldsymbol x^{(2)})'\boldsymbol w- y^{(2)},\\ \cdots,\\ \boldsymbol \phi(\boldsymbol x^{(n)})'\boldsymbol w- y^{(n)} \end{array} \right) =(ϕ(x(1)),ϕ(x(2)),⋯,ϕ(x(n))⋅ ​ϕ(x(1))′w−y(1),ϕ(x(2))′w−y(2),⋯,ϕ(x(n))′w−y(n)​ ​
= ( ϕ ( x ( 1 ) ) , ϕ ( x ( 2 ) ) , ⋯   , ϕ ( x ( n ) ) ⋅ ( ( ϕ ( x ( 1 ) ) ′ , ϕ ( x ( 2 ) ) ′ , ⋯   , ϕ ( x ( n ) ) ′ ) w − y ) =(\boldsymbol \phi(\boldsymbol x^{(1)}),\boldsymbol \phi(\boldsymbol x^{(2)}),\cdots,\boldsymbol \phi(\boldsymbol x^{(n)})\cdot (\left( %左括号 \begin{array}{c} %该矩阵一共3列，每一列都居中放置 \boldsymbol \phi(\boldsymbol x^{(1)})',\\ \boldsymbol \phi(\boldsymbol x^{(2)})',\\ \cdots,\\ \boldsymbol \phi(\boldsymbol x^{(n)})' \end{array} \right)\boldsymbol w-\boldsymbol y ) =(ϕ(x(1)),ϕ(x(2)),⋯,ϕ(x(n))⋅( ​ϕ(x(1))′,ϕ(x(2))′,⋯,ϕ(x(n))′​ ​w−y)
令 Φ = ( ϕ ( x ( 1 ) ) , ϕ ( x ( 2 ) ) , ⋯   , ϕ ( x ( n ) ) = ( ϕ 0 ( x ( 1 ) ) , ϕ 0 ( x ( 2 ) ) , ⋯   , ϕ 0 ( x ( n ) ) ϕ 1 ( x ( 1 ) ) , ϕ 1 ( x ( 2 ) ) , ⋯   , ϕ 1 ( x ( n ) ) ⋯ ϕ m ( x ( 1 ) ) , ϕ m ( x ( 2 ) ) , ⋯   , ϕ m ( x ( n ) ) ) 令\boldsymbol \Phi=(\boldsymbol \phi(\boldsymbol x^{(1)}),\boldsymbol \phi(\boldsymbol x^{(2)}),\cdots,\boldsymbol \phi(\boldsymbol x^{(n)})= \left( \begin{array}{cccc} \phi_0(\boldsymbol x^{(1)}),\phi_0(\boldsymbol x^{(2)}),\cdots,\phi_0(\boldsymbol x^{(n)}) \\ \phi_1(\boldsymbol x^{(1)}),\phi_1(\boldsymbol x^{(2)}),\cdots,\phi_1(\boldsymbol x^{(n)}) \\ \cdots \\ \phi_m(\boldsymbol x^{(1)}),\phi_m(\boldsymbol x^{(2)}),\cdots,\phi_m(\boldsymbol x^{(n)}) \\ \end{array} \right) 令Φ=(ϕ(x(1)),ϕ(x(2)),⋯,ϕ(x(n))= ​ϕ0​(x(1)),ϕ0​(x(2)),⋯,ϕ0​(x(n))ϕ1​(x(1)),ϕ1​(x(2)),⋯,ϕ1​(x(n))⋯ϕm​(x(1)),ϕm​(x(2)),⋯,ϕm​(x(n))​ ​
$\frac{\partial L(\mathbf{w})}{\partial \mathbf{w}}=\mathbf{\Phi }\cdot ({\mathbf{\Phi }}^{\prime }\mathbf{w}-\mathbf{y})$
$此外，矩阵形式的梯度计算可能可以得到更好的GPU加速$

实值函数线性基函数模型参数求解的解析解 closed form solution

$\frac{\partial L(\mathbf{w})}{\partial \mathbf{w}}=\mathbf{\Phi }\cdot ({\mathbf{\Phi }}^{\prime }\mathbf{w}-\mathbf{y})=0$
$\mathbf{\Phi }{\mathbf{\Phi }}^{\prime }\mathbf{w}-\mathbf{\Phi }\mathbf{y}=0$
$\mathbf{\Phi }{\mathbf{\Phi }}^{\prime }\mathbf{w}=\mathbf{\Phi }\mathbf{y}$
$\mathbf{w}=(\mathbf{\Phi }{\mathbf{\Phi }}^{\prime }{)}^{-1}\mathbf{\Phi }\mathbf{y}$

向量值函数广义线性模型

输出值为c个类别的评分，即c元向量，每个维度均由各自的线性函数产生
$\frac{\partial L({\mathbf{w}}_i)}{\partial {\mathbf{w}}_i}=\frac{2}{n}{\Sigma }_{p=1}^n({\hat{y}}^{(p)}-y^{(p)}){\mathbf{x}}^{(p)}=\frac{2}{n}{\Sigma }_{p=1}^n({\mathbf{w}}_i{\mathbf{x}}^{(p)}-y^{(p)}){\mathbf{x}}^{(p)}$
每个维度的权重向量${\mathbf{w}}_i$均可由上述方法求出。

Tips

1.若生成的x为特殊序列则随机梯度下降可能永远无法得到正确解，例如$(1,1,1),(2,2,2),\cdots ,(n,n,n)$，此时各维权重总是增加相同值。
2.原模型偏置bias相对样本的teaching signal较小时，总是无法得到较好解。

KNN识别CIFAR10

1NN

代码

import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
import keras
from keras.layers import Input, Dense
from keras.models import Model
from keras.optimizers import Adam
import time
"""
KNN
SVM, Softmax
Two-layer neural network
Image features
"""
cifar10 = tf.keras.datasets.cifar10
(x_train, y_train), (x_valid, y_valid) = cifar10.load_data()
x_train = x_train.reshape((50000,32*32*3))
x_valid = x_valid.reshape((10000,32*32*3))
x_valid = x_valid[0:1000]
y_valid = y_valid[0:1000]
class NearestNeighbor:
    def __init__(self):
        pass
    def train(self, X, y):
        """ X is N x D, y is 1-dimension of size N"""
        self.Xtr = X
        self.ytr = y
    def predict(self, X):
        """predict an array of patterns at one time"""
        start = time.time()
        num_test = X.shape[0]
        yPred = np.zeros(num_test, dtype = self.ytr.dtype)
        for i in range(num_test):
            print("\r{:.2f}%".format(i*100/num_test), end="")
            distances = np.sum(np.abs(self.Xtr-X[i,:]), axis = 1)#N1
            # N2
            # distances = np.linalg.norm(self.Xtr-X[i,:], ord=2, axis=1)
			# 余弦
			# distances = np.zeros(self.Xtr.shape[0])
            # for j in range(len(distances)):
            #     numerator = np.dot(X[i], self.Xtr[j])
            #     denominator = math.sqrt(np.sum(np.square(X[i])))
            #     denominator *= math.sqrt(np.sum(np.square(self.Xtr[j])))
            #     distances[j] = numerator/denominator
            min_index = np.argmin(distances)
            yPred[i] = self.ytr[min_index]
        end = time.time()
        print(f"\n耗时{end-start}s")
        return yPred
nn = NearestNeighbor()
nn.train(x_train, y_train)
yPred = nn.predict(x_valid)
num_wrong = 0
for i in range(yPred.shape[0]):
  if yPred[i] != y_valid[i]:
    num_wrong += 1
print(num_wrong)
print("accuracy is {:.2f}%".format((1-num_wrong/x_valid.shape[0])*100))

效果

方法	L1范式	L2范式	余弦距离
准确率/%	25.30	20.90	9.30

KNN

代码

import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
import math
import keras
from keras.layers import Input, Dense
from keras.models import Model
from keras.optimizers import Adam
import time
"""
KNN
SVM, Softmax
Two-layer neural network
Image features
"""
cifar10 = tf.keras.datasets.cifar10
(x_train, y_train), (x_valid, y_valid) = cifar10.load_data()
x_train = x_train.reshape((50000,32*32*3))
x_valid = x_valid.reshape((10000,32*32*3))
x_valid = x_valid[0:1000]
y_valid = y_valid[0:1000]
class KNearestNeighbor:
    def __init__(self):
        pass
    def train(self, X, y, k):
        """ X is N x D, y is 1-dimension of size N"""
        self.Xtr = X
        self.ytr = y
        self.k = k
    def getIndex(self, distances):
        n = len(distances)
        cnts = np.zeros(10)
        pivot = np.partition(distances, self.k)[self.k]
        for i in range(n):
            if distances[i] <= pivot:
                cnts[self.ytr[i]] += 1
        return np.argmax(cnts)
    def predict(self, X):
        """predict an array of patterns at one time"""
        start = time.time()
        num_test = X.shape[0]
        yPred = np.zeros(num_test, dtype = self.ytr.dtype)
        for i in range(num_test):
            print("\r{:.2f}%".format(100*i/num_test), end="")
            distances = np.sum(np.abs(self.Xtr-X[i,:]), axis = 1)
            yPred[i] = self.getIndex(distances)
        end = time.time()
        print(f"耗时{end-start}s")
        return yPred
nn = KNearestNeighbor()
for i in range(2, 10): # define range by your own
    nn.train(x_train, y_train, i)
    yPred = nn.predict(x_valid)
    num_wrong = 0
    for j in range(yPred.shape[0]):
    	if yPred[j] != y_valid[j]:
        	num_wrong += 1
    print(num_wrong)
    print("accuracy is {:.2f}%".format((1-num_wrong/x_valid.shape[0])*100))

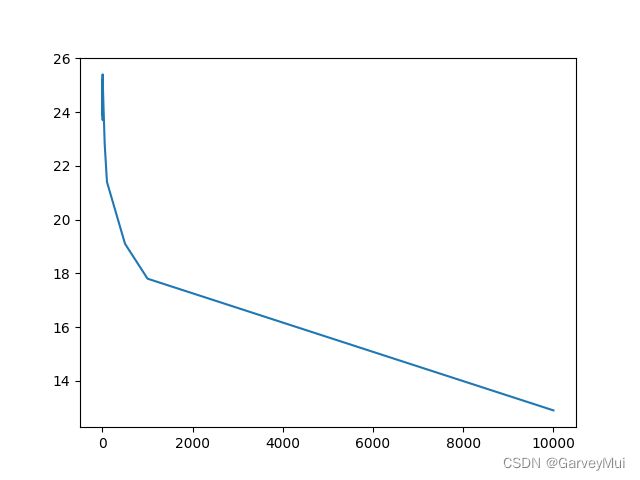
效果

使用L1范式作为测度

K	准确率/%
2	23.90
3	24.40
4	25.40
5	23.70
6	24.60
7	25.00
8	25.20
9	25.00
25	24.10
50	22.80
100	21.40
500	19.10
1000	17.80
10000	12.90