人工智能-作业3：例题程序复现

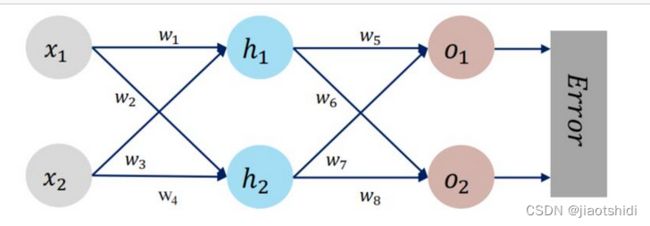
1.使用pytorch复现课上例题

运行代码

# https://blog.csdn.net/qq_41033011/article/details/109325070
# https://github.com/Darwlr/Deep_learning/blob/master/06%20Pytorch%E5%AE%9E%E7%8E%B0%E5%8F%8D%E5%90%91%E4%BC%A0%E6%92%AD.ipynb
# torch.nn.Sigmoid(h_in)

import torch

x1, x2 = torch.Tensor([0.5]), torch.Tensor([0.3])
y1, y2 = torch.Tensor([0.23]), torch.Tensor([-0.07])
print("=====输入值：x1, x2；真实输出值：y1, y2=====")
print(x1, x2, y1, y2)
w1, w2, w3, w4, w5, w6, w7, w8 = torch.Tensor([0.2]), torch.Tensor([-0.4]), torch.Tensor([0.5]), torch.Tensor(
    [0.6]), torch.Tensor([0.1]), torch.Tensor([-0.5]), torch.Tensor([-0.3]), torch.Tensor([0.8])  # 权重初始值
w1.requires_grad = True
w2.requires_grad = True
w3.requires_grad = True
w4.requires_grad = True
w5.requires_grad = True
w6.requires_grad = True
w7.requires_grad = True
w8.requires_grad = True


def sigmoid(z):
    a = 1 / (1 + torch.exp(-z))
    return a


def forward_propagate(x1, x2):
    in_h1 = w1 * x1 + w3 * x2
    out_h1 = sigmoid(in_h1)  # out_h1 = torch.sigmoid(in_h1)
    in_h2 = w2 * x1 + w4 * x2
    out_h2 = sigmoid(in_h2)  # out_h2 = torch.sigmoid(in_h2)

    in_o1 = w5 * out_h1 + w7 * out_h2
    out_o1 = sigmoid(in_o1)  # out_o1 = torch.sigmoid(in_o1)
    in_o2 = w6 * out_h1 + w8 * out_h2
    out_o2 = sigmoid(in_o2)  # out_o2 = torch.sigmoid(in_o2)

    print("正向计算：o1 ,o2")
    print(out_o1.data, out_o2.data)

    return out_o1, out_o2


def loss_fuction(x1, x2, y1, y2):  # 损失函数
    y1_pred, y2_pred = forward_propagate(x1, x2)  # 前向传播
    loss = (1 / 2) * (y1_pred - y1) ** 2 + (1 / 2) * (y2_pred - y2) ** 2  # 考虑 ： t.nn.MSELoss()
    print("损失函数（均方误差）：", loss.item())
    return loss


def update_w(w1, w2, w3, w4, w5, w6, w7, w8):
    # 步长
    step = 1
    w1.data = w1.data - step * w1.grad.data
    w2.data = w2.data - step * w2.grad.data
    w3.data = w3.data - step * w3.grad.data
    w4.data = w4.data - step * w4.grad.data
    w5.data = w5.data - step * w5.grad.data
    w6.data = w6.data - step * w6.grad.data
    w7.data = w7.data - step * w7.grad.data
    w8.data = w8.data - step * w8.grad.data
    w1.grad.data.zero_()  # 注意：将w中所有梯度清零
    w2.grad.data.zero_()
    w3.grad.data.zero_()
    w4.grad.data.zero_()
    w5.grad.data.zero_()
    w6.grad.data.zero_()
    w7.grad.data.zero_()
    w8.grad.data.zero_()
    return w1, w2, w3, w4, w5, w6, w7, w8


if __name__ == "__main__":

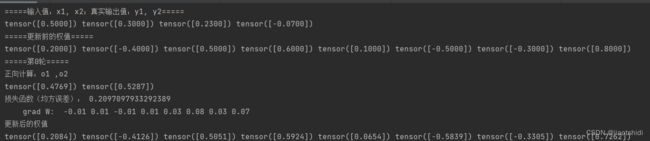
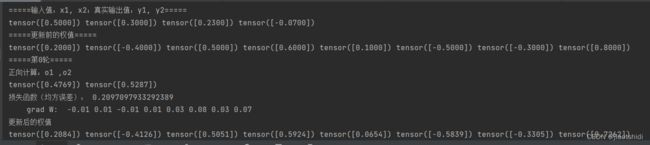
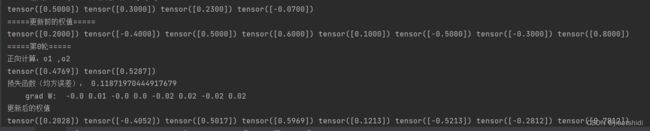
    print("=====更新前的权值=====")
    print(w1.data, w2.data, w3.data, w4.data, w5.data, w6.data, w7.data, w8.data)

    for i in range(1):
        print("=====第" + str(i) + "轮=====")
        L = loss_fuction(x1, x2, y1, y2)  # 前向传播，求 Loss，构建计算图
        L.backward()  # 自动求梯度，不需要人工编程实现。反向传播，求出计算图中所有梯度存入w中
        print("\tgrad W: ", round(w1.grad.item(), 2), round(w2.grad.item(), 2), round(w3.grad.item(), 2),
              round(w4.grad.item(), 2), round(w5.grad.item(), 2), round(w6.grad.item(), 2), round(w7.grad.item(), 2),
              round(w8.grad.item(), 2))
        w1, w2, w3, w4, w5, w6, w7, w8 = update_w(w1, w2, w3, w4, w5, w6, w7, w8)

    print("更新后的权值")
    print(w1.data, w2.data, w3.data, w4.data, w5.data, w6.data, w7.data, w8.data)

2.对比【作业3】和【作业2】的程序，观察两种方法结果是否相同？如果不同，哪个正确？

作业二代码链接
我们通过向作业二中添加代码，打印一下结果

##更新之前
print("更新前的权值")
print(w1, w2, w3, w4, w5, w6, w7, w8)
##反向传播back_propagate之后
print("\tgrad W: ", round(d_w1, 2), round(d_w2, 2),round(d_w3, 2),round(d_w4, 2),round(d_w5, 2),round(d_w6, 2),round(d_w7,2),
              round(d_w8, 2))
##更新完值后
print("更新后的权值")
print(round(w1,4), round(w2,4),round(w3,4),round(w4,4),round(w5,4),round(w6,4),round(w7,4),round(w8,4))

通过对比我们可以发现：
1、正向传播和损失函数得到的结果是一样的
2、反向传播中得到的梯度和更新后权值是不一样的

当然，作业三是正确的，作业二是自己手算的，作业三是调用的库函数。

显然是反向传播函数的推导出现了问题，重新推导一遍就发现错误了。
d_w1到d_w4的计算公式是错误的。更改成正确的之后，再次运行程序就可以发现结果是一样的

def back_propagate(out_o1, out_o2, out_h1, out_h2):    # 反向传播
    d_o1 = out_o1 - y1
    d_o2 = out_o2 - y2

    d_w5 = d_o1 * out_o1 * (1 - out_o1) * out_h1
    d_w7 = d_o1 * out_o1 * (1 - out_o1) * out_h2
    d_w6 = d_o2 * out_o2 * (1 - out_o2) * out_h1
    d_w8 = d_o2 * out_o2 * (1 - out_o2) * out_h2

    d_w1 = (d_w5 * w5 / out_h1 + d_w6 * w6 / out_h1) * out_h1 * (1 - out_h1) * x1
    d_w3 = (d_w5 * w5 / out_h1 + d_w6 * w6 / out_h1) * out_h1 * (1 - out_h1) * x2
    d_w2 = (d_w7 * w7 / out_h2 + d_w8 * w8 / out_h2) * out_h2 * (1 - out_h2) * x1
    d_w4 = (d_w7 * w7 / out_h2 + d_w8 * w8 / out_h2) * out_h2 * (1 - out_h2) * x2

    return d_w1, d_w2, d_w3, d_w4, d_w5, d_w6, d_w7, d_w8

再次贴一下调用库函数的运行结果

3.【作业2】程序更新

import numpy as np
import matplotlib.pyplot as plt


def sigmoid(z):
    a = 1 / (1 + np.exp(-z))
    return a


def forward_propagate(x1, x2, y1, y2, w1, w2, w3, w4, w5, w6, w7, w8): # 正向传播
    in_h1 = w1 * x1 + w3 * x2
    out_h1 = sigmoid(in_h1)
    in_h2 = w2 * x1 + w4 * x2
    out_h2 = sigmoid(in_h2)

    in_o1 = w5 * out_h1 + w7 * out_h2
    out_o1 = sigmoid(in_o1)
    in_o2 = w6 * out_h1 + w8 * out_h2
    out_o2 = sigmoid(in_o2)

    error = (1 / 2) * (out_o1 - y1) ** 2 + (1 / 2) * (out_o2 - y2) ** 2

    return out_o1, out_o2, out_h1, out_h2, error


def back_propagate(out_o1, out_o2, out_h1, out_h2):    # 反向传播
    d_o1 = out_o1 - y1
    d_o2 = out_o2 - y2

    d_w5 = d_o1 * out_o1 * (1 - out_o1) * out_h1
    d_w7 = d_o1 * out_o1 * (1 - out_o1) * out_h2
    d_w6 = d_o2 * out_o2 * (1 - out_o2) * out_h1
    d_w8 = d_o2 * out_o2 * (1 - out_o2) * out_h2

    d_w1 = (d_w5 * w5 / out_h1 + d_w6 * w6 / out_h1) * out_h1 * (1 - out_h1) * x1
    d_w3 = (d_w5 * w5 / out_h1 + d_w6 * w6 / out_h1) * out_h1 * (1 - out_h1) * x2
    d_w2 = (d_w7 * w7 / out_h2 + d_w8 * w8 / out_h2) * out_h2 * (1 - out_h2) * x1
    d_w4 = (d_w7 * w7 / out_h2 + d_w8 * w8 / out_h2) * out_h2 * (1 - out_h2) * x2

    return d_w1, d_w2, d_w3, d_w4, d_w5, d_w6, d_w7, d_w8


def update_w(step,w1, w2, w3, w4, w5, w6, w7, w8):    #梯度下降，更新权值
    w1 = w1 - step * d_w1
    w2 = w2 - step * d_w2
    w3 = w3 - step * d_w3
    w4 = w4 - step * d_w4
    w5 = w5 - step * d_w5
    w6 = w6 - step * d_w6
    w7 = w7 - step * d_w7
    w8 = w8 - step * d_w8
    return w1, w2, w3, w4, w5, w6, w7, w8


if __name__ == "__main__":
    w1, w2, w3, w4, w5, w6, w7, w8 = 0.2, -0.4, 0.5, 0.6, 0.1, -0.5, -0.3, 0.8 # 可以给随机值，为配合PPT，给的指定值
    x1, x2 = 0.5, 0.3   # 输入值
    y1, y2 = 0.23, -0.07 # 正数可以准确收敛；负数不行。why? 因为用sigmoid输出，y1, y2 在 （0,1）范围内。
    N = 1         # 迭代次数
    step = 1           # 步长

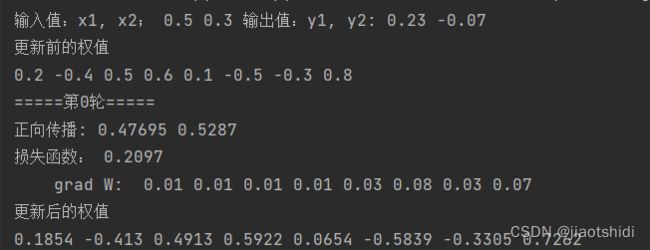
    print("输入值：x1, x2；",x1, x2, "输出值：y1, y2:", y1, y2)
    print("更新前的权值")
    print(w1, w2, w3, w4, w5, w6, w7, w8)

    eli = []
    lli = []
    for i in range(N):
        print("=====第" + str(i) + "轮=====")
        # 正向传播
        out_o1, out_o2, out_h1, out_h2, error = forward_propagate(x1, x2, y1, y2, w1, w2, w3, w4, w5, w6, w7, w8)
        print("正向传播:", round(out_o1, 5), round(out_o2, 5))
        print("损失函数：", round(error, 4))
        # 反向传播
        d_w1, d_w2, d_w3, d_w4, d_w5, d_w6, d_w7, d_w8 = back_propagate(out_o1, out_o2, out_h1, out_h2)
        print("\tgrad W: ", round(d_w1, 2), round(d_w2, 2),round(d_w3, 2),round(d_w4, 2),round(d_w5, 2),round(d_w6, 2),round(d_w7,2),
              round(d_w8, 2))
        # 梯度下降，更新权值
        w1, w2, w3, w4, w5, w6, w7, w8 = update_w(step,w1, w2, w3, w4, w5, w6, w7, w8)
        print("更新后的权值")
        print(round(w1,4), round(w2,4),round(w3,4),round(w4,4),round(w5,4),round(w6,4),round(w7,4),round(w8,4))
        eli.append(i)
        lli.append(error)


    plt.plot(eli, lli)
    plt.ylabel('Loss')
    plt.xlabel('w')
    plt.show()

4.对比【作业2】与【作业3】的反向传播的实现方法。总结并陈述

作业2中的方法通过手动计算，几乎每个过程都要自己算；作业3直接采用的张量Tensor，求Loss，构建计算图，通过backword()函数自动求梯度。自己算可能出错，能用库函数尽量用库函数，不仅代码写的简单，也保证了正确性。

5.激活函数Sigmoid用PyTorch自带函数torch.sigmoid()，观察、总结并陈述

运行结果并没有感觉到明显的区别。

6.激活函数Sigmoid改变为Relu，观察、总结并陈述

为了方便操作我们直接对sigmoid函数做如下修改

relu函数定义为：f(x) = max(0,x)，更改之后运行结果
更改之前运行结果

对比发现损失函数变成relu后训练效果明显更好了，都是经过10轮，一个的损失函数是0.11，一个是0.004。

7.损失函数MSE用PyTorch自带函数 t.nn.MSELoss()替代，观察、总结并陈述

将损失函数替换为torch.nn.MSELoss()函数：

替换之后的运行结果

对比替换之前的结果
发现梯度计算和原来的的计算结果不同，很可能是损失函数出现了错误。检查后发现少了个1/2，更改之后就一样了

torch.nn.MSELoss()是一种均方误差损失函数。正常引用就是求差的平方，其公式如下：

损失函数的讲解和使用

觉得有空写损失函数还不如自己手写，不过用函数的话可能更方便，别人一看就知道这是干什么用的。

8.损失函数MSE改变为交叉熵，观察、总结并陈述

代码实现

运行结果

和均方差的损失函数相比，计算梯度确有不同，因为很明显梯度的计算过程用的公式是不一样的。

交叉熵的讲解

9.改变步长，训练次数，观察、总结并陈述

可以参考这篇博客人工智能-作业2：例题程序复现

在合适的范围之内，增加步长或者迭代轮数都可以使损失函数减少。
不过当步长过大的时候，多轮执行，损失函数反而会变大，且会稳定在一个固定的值，再训练也没有用。
这从更新过程就可以看出，过大的步长导致对参数的修改过大，当然这和激活函数也有关系。

10.权值w1-w8初始值换为随机数，对比【作业2】指定权值结果，观察、总结并陈述

#随机函数
w=torch.rand(1)

指定值运行100轮

随机数运行100轮
初始值并不会影响算法的运行，在运行足够多的轮次之后损失函数不断下降，这就使反向传播的神奇所在吧。

11.总结反向传播原理和编码实现

反向传播算法的功能就是，给定输入和输出，在经过输入层，隐藏层和输出层，即给定路径之后，不断进行反向传播修改参数，得到我们想要的输出结果。激活函数可以增加神经网络的学习功能，损失函数是我们进行反向传播的关键因素之一，损失函数是反向传播中计算梯度计算的基础，使修改参数的依据，不同的损失函数相同的步长和初值训练的效率很可能是不同的，损失函数的选取也很重要。同时利用梯度的特性和链式法则，是反向传播的数学基础。
编码实现方面，最重要的是利用合适的工具，如pytorch中的函数库，不仅仅是为了我们方便，减少我们自己的出错，更是方便他人的阅读，和自己的检查修改，所以能用已有的函数，尽量使用。

12.参考链接

【2021-2022 春学期】人工智能-作业3：例题程序复现 PyTorch版
【人工智能导论：模型与算法】MOOC 8.3 误差后向传播(BP) 例题 编程验证

人工智能-作业2：例题程序复现

【pytorch函数笔记（四）】torch.nn.MSELoss()

损失函数——交叉熵损失函数（CrossEntropy Loss）