A Survey of Optimization Methods from a Machine Learning Perspective
原文地址:https://arxiv.org/abs/1906.06821
Abstract摘要
机器学习发展迅速,在理论上取得了许多突破,并广泛应用于各个领域。优化作为机器学习的重要组成部分。随着数据量的指数增长和模型复杂性的增加,机器学习中的优化方法面临越来越多的挑战。相继提出了许多解决机器学习中的优化问题或改进优化方法的工作。从机器学习的角度对系统优化方法进行系统的回顾和总结具有重要意义,可以为优化的发展和机器学习研究提供指导。在本文中,我们首先描述了机器学习中的优化问题。然后,我们介绍了常用优化方法的原理和进展。接下来,我们总结一些优化方法在一些流行的机器学习领域中的应用和发展。最后,我们探索并提出了一些挑战和尚未解决的问题,以优化机器学习。
1. Introduction简介
从优化的梯度信息的角度看,一般可分为三类:first-order optimization methods(一阶优化方法)以随机梯度方法为代表、high-order optimization methods(高阶优化方法)以牛顿法为代表、 heuristic derivative-free optimization methods(启发式无导数优化方法)以协调下降法为代表。
2. 优化的机器学习
几乎所有的机器学习算法都可以表述为一个优化问题,以求出目标函数的极值。根据建模目的和要解决的问题,机器学习算法可分为监督学习,半监督学习,无监督学习和强化学习。监督学习又分为分类问题和回归问题,无监督学习分为聚类和降维。
2.1监督学习的优化问题
监督学习的优化问题,实质上是找到一个映射函数f(x)来最小化损失函数。
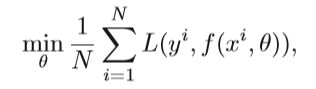
N是训练样本的数量, θ 是映射函数的参数,xi是第i个样本的特征向量,yi是相应的标签,监督学习中有多种损失函数,如欧式距离、交叉熵、对比损失、信息增益等,回归问题最简单的就是用欧式距离的平方、在目标函数上,通常会添加正则项减轻过拟合,例如L2范式:
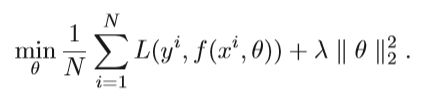
2.2半监督学习的优化问题
半监督学习实质上就是综合了监督学习和无监督学习,其中既有带标签的样本,也有不带标签的样本,它可以处理不同的任务,包括分类,回归,聚类,和降维。文中以semi-supervised support vector machines (S3VM)为例,优化过程如下:
将部分训练集标记为:
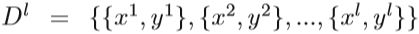
未标记的数据表示为:
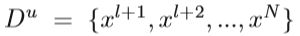
其中N=l+u;对未标记的数据添加附加约束ζi,其中,如果真实标签为正,则将εi定义为未标记实例的错误分类错误;如果真实标签为负,则将zj定义为未标记实例的错误分类错误。S3VM问题可以描述为:
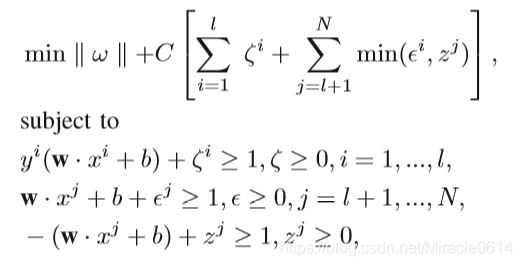
其中,C是惩罚系数,这个方程是比较难解的,可以用后面提到的分支界定法和凸松弛法进行简化。
2.3无监督学习的优化问题
聚类算法就是将样本分为多个簇,使同一个簇之间的样本差异尽可能小,不同簇之间的样本差异尽可能大,K-means算法的优化问题就是最小化损失函数:
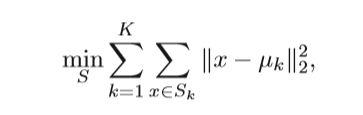
K是簇的个数,x是样本的特征向量,uk是第k个簇的中心。
降维算法可确保将数据中的原始信息投影到低维空间后将其保留得尽可能多
Principal component analysis(PCA)为典型例子:
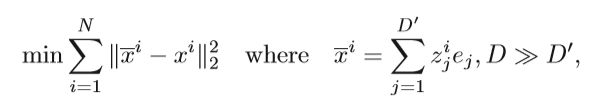
xi是D维向量, X i Xi Xi 是 xi的重建,zi是xi在D’上的投影,ej是D’维上的标准正交基。
概率模型中另一个常见的优化目标是找到p(x)的最佳概率密度函数,该函数最大化训练样本的对数似然函数(MLE)
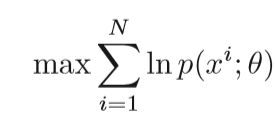
在贝叶斯框架中,通常会对θ假设一些先验分布,以此来减轻过拟合。
2.4强化学习中的优化问题
与有监督学习和无监督学习不同,强化学习的目的是找到一种最优策略功能,其输出随环境而变化。
对于确定性策略,从状态s到动作a的映射函数是学习目标。
对于不确定的策略,执行每个动作的概率是学习目标。
在每种状态下,操作由a =π(s)确定,其中π(s)是策略函数。
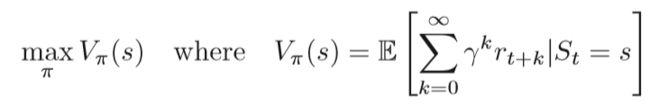
Vπ(s)是在策略π下状态s的函数, γ 是折现因子
3.基本的优化方法和发展
**
A、一阶的方法
在机器学习领域,最常用的一阶优化方法主要基于梯度下降。 在本节中,我们将介绍一些代表性算法以及梯度下降方法的发展。
1、梯度下降:
梯度下降法的思想是变量在目标函数梯度的(相反)方向上迭代更新。 执行更新以逐渐收敛到目标函数的最佳值。 学习速率η决定每次迭代的步长,因此影响迭代次数以达到最佳值。对于线性回归模型,我们假设fθ(x)是要学习的函数,L(θ)是损失函数,θ是要优化的参数。 目标是最大程度地减少损失函数。
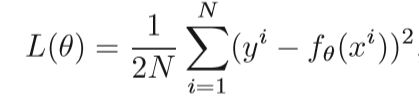
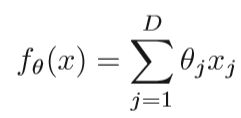
N是训练样本的数量,D是输入特征的数量,xi是独立的变量,yi是目标输出,梯度下降交替执行下两步,直至收敛:
(1)推导L(θ)对θj的偏导
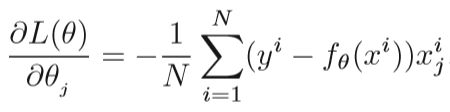
(2)在负梯度方向更新每个θj
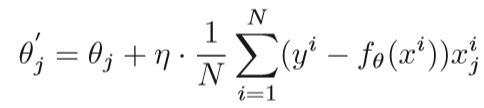
如果样本的数量是N,x的维度是D,每一次迭代的计算复杂度是O(ND),在处理大规模数据时难以接受,因此提出随机梯度下降(SGD)
2、 Stochastic Gradient Descent(SGD):随机梯度下降的思想是随机使用一个样本来更新每次迭代的梯度,而不是直接计算梯度的确切值,从而加快收敛速度,上述的损失函数可以表示为:
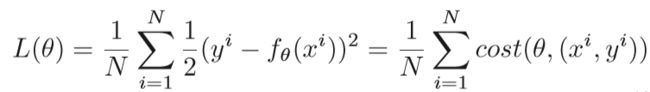
如果在SGD中选择一个随机样本i,则损失函数L*(θ):
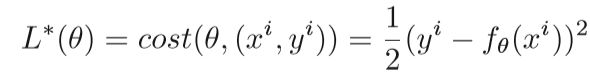
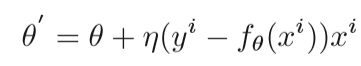
很显然的可以看出与上式梯度下降的区别,由于SGD每次迭代仅使用一个样本,因此每次迭代的计算复杂度为O(D),但是,SGD中的一个问题是,由于随机选择引入的附加噪声,梯度方向会振荡,并且搜索过程在解空间中是盲目的。 与批次梯度下降总是沿梯度的负方向移向最佳值不同,SGD中的梯度变化较大,SGD中的移动方向存在偏差。 因此,提出了两种方法之间的折衷,即小批量梯度下降方法(MSGD)
MSGD使用b个独立的均匀分布的样本(b通常在50到256中)作为样本集来更新每次迭代中的参数。 此外学习率的选择也很重要,太小的学习率将导致较慢的收敛速度,而太高的学习率将阻碍收敛,使损失函数最小化。解决此问题的一种方法是建立预定的学习率列表或某个阈值,并在学习过程中调整学习率。除了学习率外,如何避免目标函数陷入局部最小值的无限个数中也是一个普遍的挑战。 这种困难不是来自局部最小值,而是来自“鞍点” 。 鞍点的斜率在一个方向上为正,在另一个方向上为负,并且所有方向上的坡度值为零。 SGD摆脱这些问题是一个重要的问题。
3、 Nesterov Accelerated Gradient Descent(NAG):介绍NAG之前,要先了解动量法,NAG是在动量法的基础上演变而来的。动量的概念源自物理力学,它模拟物体的惯性。实则上就是保持上一次迭代对下次迭代的影响,在梯度下降方法中,每次的速度更新为v =η·(-∂L(θ)/∂(θ))。使用动量算法,更新量v不仅仅是通过η·(-∂L(θ)/∂(θ))计算出的梯度下降量。 它还考虑了摩擦系数,该系数表示为先前的更新vold乘以[0,1]范围内的动量因子:
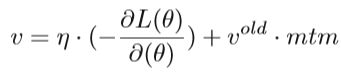
mtn是动量因子,通过公式可以看出如果当前梯度与先前的速度平行,vold可以加快v,当学习率η较小时,适当的动量在加速收敛中起作用。 如果导数衰减到0,它将继续更新v以达到平衡。同样的,如果当前梯度与之前的速度反向,vold可以减缓v的更新,经过试验证明,mtn选择0.9大多数情况是最佳的。下图可以更直观的理解动量法:
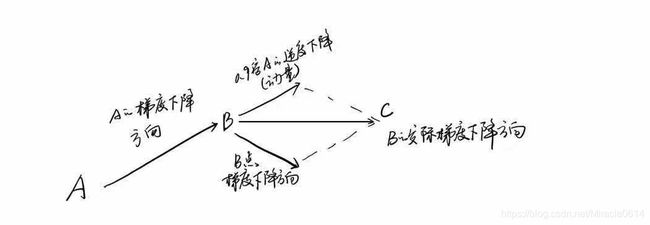
NAG在此基础上进行了改进,
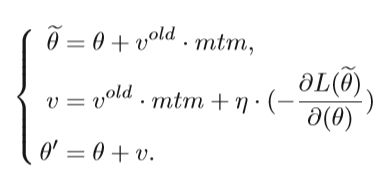
Nesterov动量相对于传统动量法的改善反映在更新未来位置而非当前位置的梯度上。 如下图所示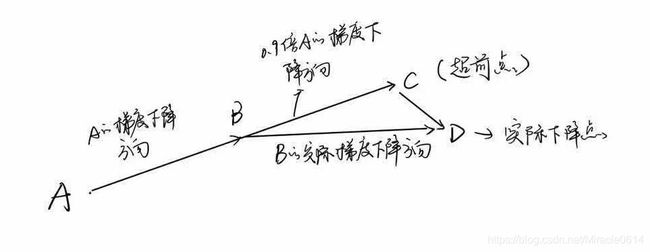
另一个因素是如何定义学习率的大小,如果搜索更接近最佳点,则更有可能发生振荡。学习速率衰减因子d通常用于SGD的动量法中,这会使学习速率随迭代周期而降低。
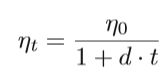
其中ηt是第t次迭代的学习率,η0是原始学习率,d属于[0,1],d越小,衰减越慢。
4、Adaptive Learning Rate Method
手动调节学习率很多情况下会极大影响学习效果,自适应的方法无需进行参数调整,收敛速度很快,并且通常可以获得不错的结果。SGD最直接的改进是AdaGrad,AdaGrad在某些先前的迭代中根据历史梯度动态调整学习率。 公式如下:
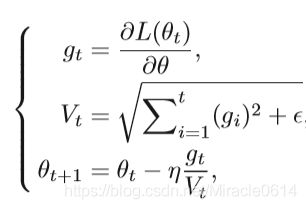
其中gt是迭代t时参数θ的梯度,Vt是迭代t时参数θ的累积历史梯度,θt是迭代t时参数θ的值。
AdaGrad和梯度下降之间的区别在于在参数更新过程中,学习率不再固定,而是使用直到此迭代之前累积的所有历史梯度来计算的,消除了手动调整学习速率的需要。 大多数实现对η使用默认值0.01。
尽管AdaGrad自适应地调整学习速度,但仍然存在两个问题。 1)该算法仍然需要手动设置全局学习率η。 2)随着训练时间的增加,累积的梯度会越来越大,使学习率趋于零,从而导致无效的参数更新。
AdaGrad被进一步改进为AdaDelta和RMSProp,以解决学习率最终变为零的问题。主要想法是不累计所有历史梯度,并使用指数移动平均值来计算二阶累积动量
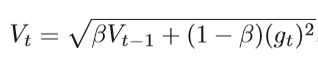
其中β是指数衰减参数
Adaptive moment estimation(自适应矩估计) 是另一种SGD方法,它为每个参数引入了自适应学习率。 它结合了自适应学习率和动量方法。 除了存储像AdaDelta和RMSProp这样的过去平方梯度Vt的指数衰减平均值外,Adam还保留了过去梯度mt的指数衰减平均值,类似于动量法:
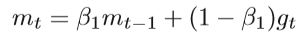
Momentum项:更新一阶矩估计
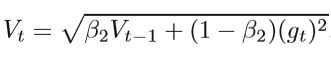
RMSProp项:更新二阶矩估计。
其中β1和β2是指数衰减率。 参数θ的最终更新公式为:
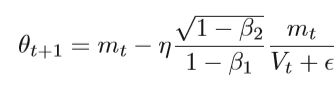
(上式原论文中的第一个mt应该为θt,作者书写失误)
5、 Variance Reduction Methods: 由于训练样本中包含大量冗余信息,因此自提出以来,SGD方法就非常受欢迎。 但是,随机梯度法只能以亚线性速率收敛,并且梯度的方差通常很大。 如何减少方差并提高SGD到线性收敛一直是一个重要的问题。
Stochastic Average Gradient(SAG) 随机平均梯度法(SAG)是一种减少方差的方法,SAG算法保持参数d记录中N个最新梯度{gi}的和,其中gi是使用一个样本i,i∈{1,…,N}计算的。 详细的实现是选择一个样本以随机更新d,并在迭代t中使用d更新参数θ:
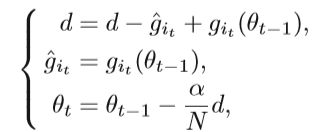
在迭代t中通过用新的梯度git(θt-1)替换d中的旧梯度git来计算更新的d,α是代表学习率的常数,因此,每次更新仅需要计算一个样本的梯度,是一种节省空间的典型方式,速度上要比SGD快得多,并且是线性收敛的方式。但是,SAG方法仅适用于损失函数平滑且目标函数为凸(例如凸线性预测问题)的情况。
Stochastic Variance Reduction Gradient(SVRG)
由于SAG方法仅适用于光滑函数和凸函数,并且需要存储每个样本的梯度,因此在非凸神经网络中应用不方便。 为了提高复杂模型的优化性能,提出了SVRG方法。SVRG算法通过计算每w次迭代而不是每次迭代中所有样本的梯度来维持区间平均梯度:
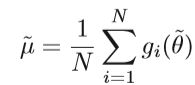
其中 θ ~ θ \widetilde{θ} θ θ θ是间隔更新参数。
∇F(θ)=Aθ-b
θt+1 = θt + ηtdt
ηt的更新公式为:
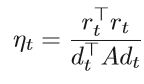
搜索方向dt是通过负残差和先前搜索方向的线性组合获得的,即:
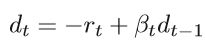
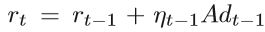
标量βt是更新参数,可以通过满足dt和dt-1关于A共轭的要求来确定,即
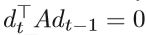
由上述各式可以得出
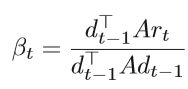
进一步推导得出
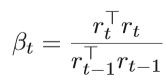
公式有点抽象,具一个实际的例子结合上述公式进行理解:
例如有三维的情况,想象有一个西瓜,它的内部每一点处有某一种性质,比如说甜度,假设它在正中心处甜度最高,最外面是瓜皮最不甜,依次往里甜度是呈抛物增长的。那么,我们拿一把刀,给它切一刀(不一定对半),会形成一个切面,那么这个切面是个椭圆,且在椭圆的正中间是最甜的(极值点),拿一根牙签,从这个最甜的点垂直切面往里面一戳,这个方向就是这一点负梯度方向。当然,也不一定能正好西瓜正中心。这应该就是最速下降与共轭梯度的区别。还是以切西瓜为例:
首先我们拿一根足够长的牙签沿着西瓜任意位置将它穿透,那么前面的性质告诉我们没在西瓜中的牙签的中点就是这根牙签上的最值点。(这其实就是最速下降方法的步骤,最速下降法往往是沿着一个方向取到最小,步长以此来决定,接着换一个方向,同样一个过程……)
接着找到最值点(牙签中点)的梯度方向,最速下降法就是以梯度方向接着找最小值点,但我们现在不这么做。梯度方向和原来的牙签的方向形成了一个面,我们试图在这个面里面找一个更好的方向。前面的性质告诉我们,这个切面的中点是这个面的最小值点,那么我就应该以牙签中点和这个切面的连线作为方向是最理想的。
问题是这个切面的中点不好找,好在前面的性质告诉我们,这个切面的中点的梯度方向是垂直于这个切面的,把提到的这几个条件联立起来,其实很快就能找到牙签中点和切面中点的连线方向,以及我们所需要的步长。
CG方法具有很好的性质,仅使用先前的向量dt-1生成新的向量dt,而不必知道所有先前的向量d0,d1,d2 … dt-2,具体的算法实现见Algorithm 2 :

2) Quasi-Newton Methods
梯度下降采用一阶信息,但收敛速度较慢。 因此,自然的想法是使用二阶信息,例如牛顿方法。 牛顿方法的基本思想是同时使用一阶导数(梯度)和二阶导数(Hessian矩阵)以二次函数逼近目标函数,然后求解二次函数的最小优化。 重复此过程,直到更新的变量收敛为止。首先介绍一维牛顿法:
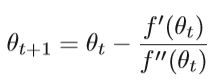
f是目标函数,更一般的高维牛顿法的迭代公式为:
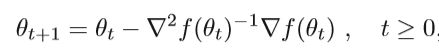
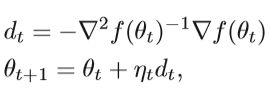
其中dt是牛顿方向,ηt是步长。 这种方法可以称为阻尼牛顿法。 从几何学上讲,牛顿法是用二次曲面拟合当前位置的局部表面,而梯度下降法是用平面拟合当前局部的表面。
Quasi-Newton Method
牛顿法是一种迭代算法,需要在每个步骤计算目标函数的逆Hessian矩阵,这使得存储和计算非常复杂。 为了克服昂贵的存储和计算,考虑了一种近似算法,称为拟牛顿法。 拟牛顿法的基本思想是使用正定矩阵近似Hessian矩阵的逆,从而简化了运算的复杂性。 拟牛顿法是解决非线性优化问题的最有效方法之一。拟牛顿法不需要直接使用二阶梯度,因此有时比牛顿法更有效。 在下面的部分中,将介绍几种拟牛顿法,用不同的方法对Hessian矩阵及其逆矩阵进行近似。
Quasi-Newton Condition
首先介绍拟牛顿法的条件,假定目标函数f可以由二次函数近似,我们可以将f(θ)扩展到θ=θt+ 1的泰勒级数,即:
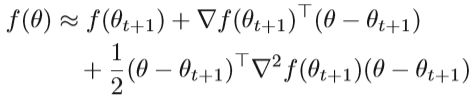
对上式左右两边同时求梯度,得出近似解:
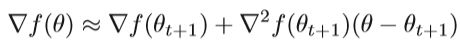
令θ=θt
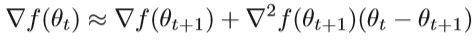
用B代表近似的黑森矩阵,st=θt+1-θt, ut= ∇ ∇ ∇ ∇\nabla ∇ ∇∇∇f(θt+1)- ∇ ∇ ∇ ∇ \nabla∇ ∇∇∇f(θt)
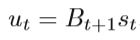
这个等式就是拟牛顿条件或者割线方程
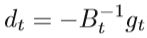
dt就是拟牛顿法的搜索方向,其中gt是f的梯度,拟牛顿法的更新为:
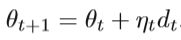
选择步长ηt以满足Wolfe条件,这是不精确线搜索minηtf(θt+ηtdt)的一组不等式。与牛顿方法不同,拟牛顿方法使用Bt近似真实的黑森矩阵。下式为Wolfe-Powell准则:
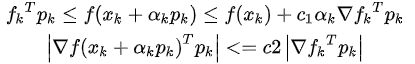
在下面的段落中,我们将介绍一些特殊的拟牛顿法,其中Ht用于表示Bt的逆。
DFP DFP是第一种拟牛顿法,以三位提出者的首字母命名,具体的公式如下:
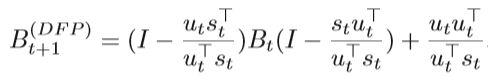
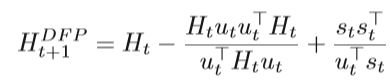
BFGS Broyden, Fletcher, Goldfarb and Shanno 提出了 BFGS method
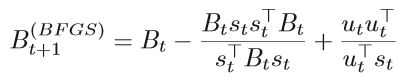
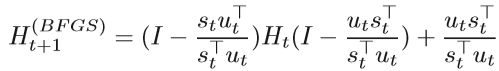
拟牛顿法仍然无法解决大规模数据优化问题,因为该方法会生成一系列矩阵以逼近Hessian矩阵。 存储这些矩阵需要消耗计算机资源,尤其是对于高维问题。 将这些矩阵保留在计算机的高速存储中也是不可能的,从而限制了它对中小型问题的使用。
L-BFGS Limited memory quasi-Newton methods,称为L-BFGS,是基于拟牛顿法的改进,在处理高维情况时是可行的。 该方法仅存储几个n维向量,而不是保留和计算Hessian 的全部n×n近似值。 L-BFGS的基本思想是在近似H~t + 1的计算中存储矢量序列,而不是存储完整的矩阵Ht~。 L-BFGS进一步合并了H~t + 1~的更新公式:
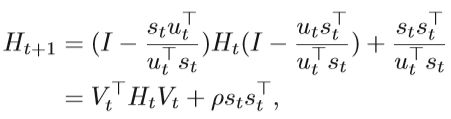
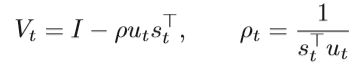
上面的等式意味着可以使用序列对{sl,ul} tl=t-p+1来获得逆海森近似Ht+1。 如果我们知道对{sl,yl} tl=t-p+1,则可以计算H~t + 1~。 换句话说,除了存储和计算完整的矩阵Ht+1之外,L-BFGS仅计算{sl,yl}的最新p对。根据等式,可以实现递归过程。 当保留最新的p步时,Ht+1的计算可表示为:
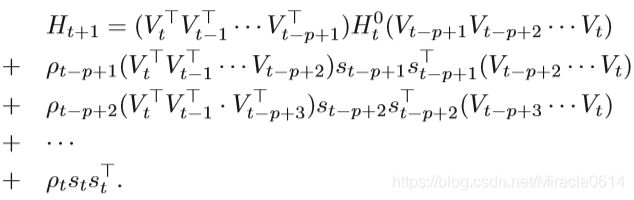
可以计算出更新方向dt= Htgt,其中gt是目标函数f的梯度。 详细的算法显示在算法3和4中。


3) Stochastic Quasi-Newton Method
在许多大型机器学习模型中,有必要使用随机近似算法,每个更新步骤都基于相对较小的训练子集。 随机算法通常在大规模学习系统中获得最佳的泛化性能。 拟牛顿法仅使用一阶梯度信息来近似Hessian矩阵。 将准牛顿法与随机法相结合是一个自然的想法,Online-BFGS和online-LBFGS是BFGS的两个变体。
考虑凸函数的最小化:
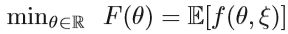
ξ是随机种子。假设ξ代表一个由输入输出对(x,y)组成的样本(或一组样本)。x表示输入,y是目标输出。 f通常具有以下形式:
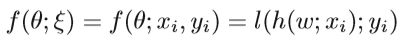
其中h是由θ参数化的预测模型,而l是损失函数。我们定义
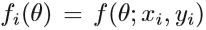
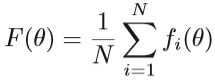
通常,如果使用大量训练数据来训练机器学习模型,则更好的选择是使用小批量随机梯度:
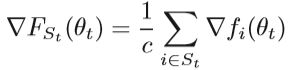
子集St是随机选择的,C<tH是训练样本的随机子集,那么Hessian矩阵的估计是:
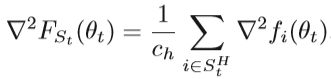
将ut,st修改为:
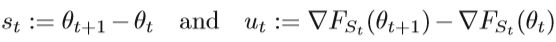
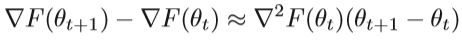
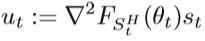
详细的算法如下Algorithm 5:

在上述算法中,V = {st,ut}是m对的集合,gt是当前随机梯度∇FSt(θt)
此外,在线L-BFGS提出,提出了一种线性收敛方法,该方法将L-BFGS方法与方差减少技术相结合。 除此之外,还提出了一种方差缩减块L-BFGS方法,该方法通过对一组随机向量采用二次采样Hessian的作用来工作。综上,讨论了在二阶优化中使用随机方法的技术。 随机拟牛顿法是随机方法和拟牛顿法的结合。
4) Hessian-Free Optimization Method
HF方法的主要思想类似于牛顿方法,后者采用二阶梯度信息。 不同之处在于,HF方法无需直接计算Hessian矩阵。它通过某些技术估算H,因此被称为“ Hessian free”。考虑对象F围绕参数θ的局部二次逼近Qθ(dt):
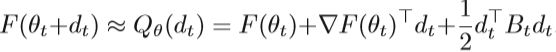
dt是搜索方向。 HF方法采用共轭梯度法来计算线性系统的近似解dt
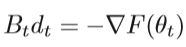
Bt=H(θt)是Hessian矩阵,但是实际上Bt经常被定义为Bt=H(θt)+λI, λ ≥ 0,具体的算法框架如下图:

使用共轭梯度法的优点是它可以计算Hessian向量乘积而无需直接计算Hessian矩阵。 因为在CG算法中,Hessian矩阵与向量配对,所以我们可以计算Hessian向量乘积来避免计算Hessian逆矩阵。 有多种计算Hessian向量积的方法,其中一种方法是通过有限差分计算:
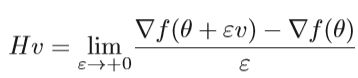
Sub-sampled Hessian-Free Method
HF在应用于具有大规模数据的深度神经网络时存在不足之处。 因此,在HF中采用了子采样技术,从而形成了一种有效的HF方法。 通过仅使用小的样本集S来计算Hv,可以减少每次迭代的成本。 目标函数具有以下形式:
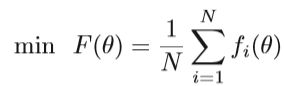
在第t次迭代中,随机梯度估计可以写为:
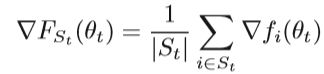
随机Hessian估计表示为:
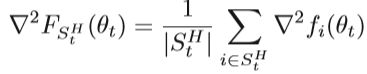
如上所述,可以通过使用CG方法求解线性系统来获得方向dt的近似解,其中使用了随机梯度和随机Hessian矩阵。
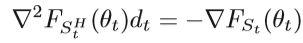
一个问题是如何确定StH的大小。 一方面,StH可以选择得足够小,以使CG迭代的总成本不会比梯度评估大多少。 另一方面,StH应该足够大以从Hessian矢量积中获得有用的曲率信息。 如何平衡StH的大小是一个正在研究的挑战。
Natural Gradient
传统的梯度下降算法基于欧式空间。 但是在许多情况下,参数空间不是欧式空间,并且可能具有黎曼度量结构。 在这种情况下,目标函数的最陡方向不能由普通梯度给出,而应由自然梯度给出。
设定模型分布为p(y | x,θ),π(x,y)为经验分布。 我们需要拟合参数θ∈RN。 假设x是观察向量,y是其关联的标签。 它的目标函数如下:
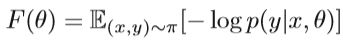
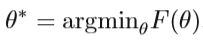
自然梯度可以从传统梯度乘以Fisher信息矩阵,即
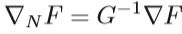
其中F是目标函数, ∇ ∇ ∇ ∇ \nabla∇ ∇∇∇NF是自然梯度, ∇ ∇ ∇ ∇ \nabla∇ ∇∇∇F是传统梯度, G − 1 G − 1 G − 1 G−1G^{-1} G−1 G−1G−1G−1是Fisher information
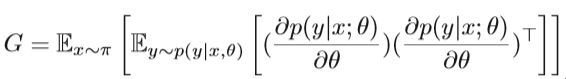
自然梯度的更新与传统梯度的更新类似:

不能忽视的是自然梯度的应用非常有限,因为计算量太大。 估计Fisher信息矩阵并计算其逆矩阵是庞大的计算量。 为了克服这一限制,开发了truncated Newton’s method,其中通过迭代过程计算逆,从而避免了直接计算Fisher信息矩阵的逆。 此外, factorized natural gradient (FNG)和 Kronecker-factored approximate curvature (K-FAC)方法被提出,该方法使用概率模型的导数来计算近似自然梯度更新。
6) Trust Region Method:
上面介绍的大多数方法的更新过程可以描述为θt+ηtdt。 点在dt方向上的位移可以写为st。 典型的信赖域方法(TRM)可用于无约束的非线性优化问题,其中位移st是直接确定的。对于问题minfθ(x),TRM 使用二阶泰勒展开来逼近目标函数fθ(x),表示为qt(s)。每次搜索均在半径为△t的信任区域范围内进行。 这个问题可以描述为:
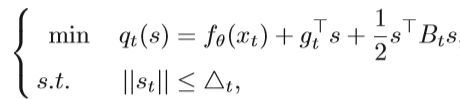
其中gt是目标函数f(x)在当前迭代点xt处的近似梯度,Bt是对称矩阵,是Hessian矩阵的近似值,且△t> 0是信任区域的半径,如果在约束函数中使用L2范数,它将成为Levenberg-Marquardt算法,在每个更新过程中,测量二次模型q(st)与目标函数fθ(x)的相似度,并动态更新△t。 第t次迭代的实际下降量为:
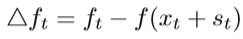
第t次迭代的预测下降为:
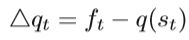
比率rt定义为测量两者的近似程度:
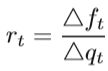
这表明,当rt接近1时,该模型比预期的更为实际,因此我们应考虑扩展△t。 同时,它表明当rt接近0时,该模型预测较大的下降,而实际下降较小,则应减小△t。 此外,如果rt在0到1之间,我们可以保持△t不变。
C. Derivative-Free Optimization
对于实际应用中的一些优化问题,目标函数的导数可能不存在或不容易计算。 在这种情况下,找到最佳点的解决方案称为无导数优化,无导数优化的思路主要有两种。一种是使用启发式算法。它以经验法则为特征,包括经典的模拟退火算法,遗传算法,蚁群算法和粒子群优化。这些启发式方法通常会产生近似的全局最优值。本节不关注此类技术。另一种是根据目标函数的样本来拟合一个函数。这种类型的方法通常将一些约束条件附加到搜索空间以得出样本。坐标下降法是一种典型的无导数算法。
坐标下降法是针对多变量函数的无导数优化算法。 其思想是可以沿每个轴方向顺序执行一维搜索,以获得每个维的更新值。 此方法适用于损失函数不可微的某些问题。普通方法是在线性空间中选择一组基数e1,e2,…,eD作为搜索方向,并在每个方向上最小化目标函数的值。 对于目标函数L(Θ),当已经获得Θt时,Θt+1的第j维可通过下式获得:
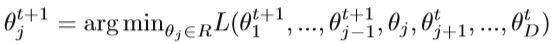
该方法的收敛性类似于梯度下降方法。 更新的顺序可以是每次迭代中从e1到eD的任意排列。 下降方向可以从坐标轴到坐标块进行概括,坐标下降与梯度下降之间的主要区别在于 梯度下降方法中的每个更新方向均由当前位置的梯度确定,该位置可能不平行于任何坐标轴。在坐标下降法中,优化方向从头到尾固定。它不需要计算目标函数的梯度。在每次迭代中,更新仅沿一个轴的方向执行,因此即使对于一些复杂的问题,坐标下降法的计算也很简单。对于不可分割的函数,可以使用适当的坐标系来加速收敛。例如,自适应坐标下降法采用PCA来获得新的坐标系,坐标之间的相关性越小越好。在执行非平滑目标函数时,坐标下降法仍然存在局限性,可能会落入非平稳点。
D. Preconditioning in Optimization
预处理是优化方法中非常重要的技术。 合理的预处理可以减少优化算法的迭代次数。 可以简单地认为预处理是将困难的线性系统Aθ= b转换为具有相同解但具有更好光谱特性的等效系统。 例如,如果M是系数矩阵A的非奇异近似,
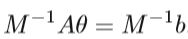
上式与Aθ= b具有相同的解,但是上式可能更容易求解,系数矩阵M-1A的求解可能更有利。
在大多数线性系统中,例如Aθ= b,矩阵A通常很复杂,很难求解该系统。 因此,需要进行一些转换以简化此系统,M就是预处理条件。前面提到的共轭梯度算法(CG)是预处理技术中最常用的优化方法,它可以加快收敛速度。
4、机器学习领域的发展和应用
面对不同的机器学习问题和特定的应用环境,进一步开发了许多优化方法。这一节主要包括deep neural networks, reinforcement learning, variational inference and Markov chain Monte Carlo.
A. Optimization in Deep Neural Networks
DNN的优化方法有很多,依然从一阶和高阶两个方面进行分析。
1) First-Order Gradient Method in Deep Neural Networks:
随机梯度优化方法及其自适应变量已在DNN中得到广泛应用,并取得了良好的性能。 SGD引入了学习率衰减因子,AdaGrad累积了所有以前的梯度,但是这两种方法的学习速度使优化的后期更新速度变慢。 AdaDelta,RMSProp,Adam和其他方法使用指数平均来提供有效的更新并简化计算。这些方法使用指数移动平均数来缓解由于学习率快速衰减而引起的问题,但限制了当前学习率只能依靠一些梯度。 几乎所有依赖过去梯度的固定大小的算法都会遇到此问题,包括AdaDelta和Nesterov加速自适应矩估计(Nadam)。最好依靠过去渐变的长期记忆,而不是渐变的指数移动平均值以确保收敛。 Adam的新版本称为AmsGrad,它使用一种简单的校正方法来确保模型的收敛性,同时保留原始的计算性能和优势。 与Adam方法相比,AmsGrad对一阶矩估计和二阶矩估计进行了以下更改:
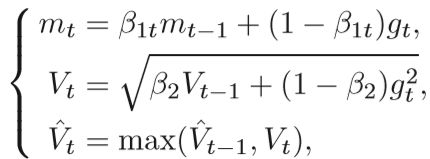
其中β1t是随时间减小的非常数,β2是恒定的学习率。 在二阶矩Vt中进行校正,使 V ^ t V t \widehat {V}~t~ V t V t V t 单调。 V ^ t V t \widehat {V}~t~V t V t V t 实际上用于目标函数的迭代中。 AmsGrad方法采用基于Adam方法的过去梯度的长期存储,保证了后期的收敛性,并且在应用中效果很好。同时更新β1、β2有利于一定程度的收敛,β1和β2可以设置为:β1t=β1/t,β1t≤t,β2t=1-1/t。
提出了将SGD和Adam结合使用的另一种想法,以解决自适应梯度算法的不收敛问题。 自适应算法(例如Adam)收敛速度很快,适合处理稀疏数据。 具有动力的SGD可以收敛到更准确的结果。 SGD和Adam的结合开发了两种方法的优势。 具体来说,它首先与Adam训练,然后根据先前的参数在适当的切换点快速切换到SGD以进行精确优化。 该策略被称为从Adam切换到SGD(SWATS)。 SWATS中存在两个核心问题。 一种是何时从Adam切换到SGD,另一种是在切换优化算法后如何调整学习率。 下文将详细介绍SWATS方法,Adam迭代t次时参数的运动dAdam为:
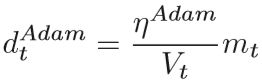
ηAdam 是Adam的学习速率
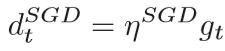
ηSGD是SGD的学习速率,gt是当前位置的梯度。SGD的运动可以分解为沿着Adam方向及其正交方向的学习率。 如果SGD将要完成轨迹,但在选择优化方向后由于动量而未完成Adam,则SWATS是一个不错的选择。 同时,SWATS还通过沿正交方向移动来调整其优化轨迹。使得:
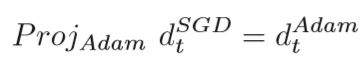
其中ProjAdam表示朝Adam方向的投影。
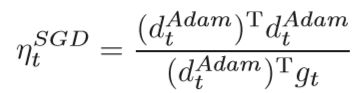
为了减少噪声,可以使用移动平均值校正学习率的估计值
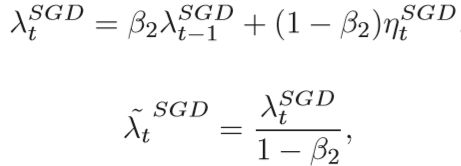
λtSGD是学习速率ηSGD的第一时刻,第二式是SGD收敛后的学习速率,转换点的选择,通常用一个简单的标准:
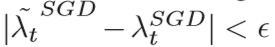
没有严格的数学证明可用于选择此转换标准,但它在各种应用程序中的性能都很好。SWATS基于Adam,此切换方法也适用于其他自适应方法,例如AdaGrad和RMSProp。 该过程对超参数不敏感,可以获得与SGD相当的最佳解决方案,但在深度网络的情况下具有更快的训练速度。
一般的完全连接的神经网络无法处理诸如文本和音频之类的顺序数据。 递归神经网络(RNN)是一种更适合于处理顺序数据的神经网络。 通常认为,使用一阶方法来优化RNN是无效的,因为SGD及其变体方法很难学习序列问题中的长期依赖性。近年来用于训练RNN的一阶优化方法已经得到发展,但是它们仍然面临着深度RNN收敛缓慢的问题。 采用曲率信息的高阶优化方法可以使收敛速度接近最佳值,并且被认为在优化DNN方面更为有效。
2) High-Order Gradient Method in Deep Neural Networks:
为了充分利用梯度信息,将二阶方法逐渐应用于DNN。主要介绍DNN中的Hessian-Free方法。前面已经对Hessian-free(HF)进行了研究,但它并不直接适用于处理神经网络。 由于DNN中的目标函数不是凸函数,因此精确的Hessian矩阵可能不是正定的。 因此,需要进行一些修改,以便将HF方法应用于神经网络。
The Generalized Gauss-Newton Matrix
广义高斯-牛顿(GGN)矩阵,可以将其视为Hessian矩阵的近似值,它是可证明的正半定矩阵,避免了负曲率的麻烦。 至少有两种方法可以得出GGN矩阵。 它们都要求f(θ)可以表示为两个函数的组合,写为f(θ)= Q(F(θ)),其中f(θ)是目标函数,Q是凸函数。 GGN矩阵G采用以下形式:
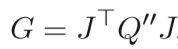
J是F的雅各比矩阵。
补充一个知识,什么是雅各比矩阵。雅可比矩阵是一阶偏导数以一定方式排列成的矩阵。其行列式称为雅可比行列式。假设F: Rn→Rm是一个从欧式n维空间转换到欧式m维空间的函数。这个函数F由m个实函数组成: y1(x1,…,xn), …, ym(x1,…,xn)。这些函数的偏导数(如果存在)可以组成一个m行n列的矩阵, 这就是所谓的雅可比矩阵
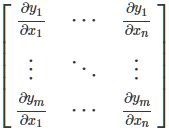
可以表示为:
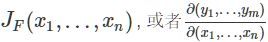
下面在维基百科上找了个例子:

Damping Methods
HF方法的另一种修改是使用不同的阻尼方法。 例如,Tikhonov阻尼是最著名的阻尼方法之一,它是通过将二次惩罚项引入二次模型来实现的。 将二次惩罚项λ/2*d⊤d添加到二次模型中。
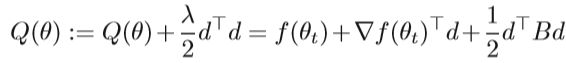
其中B = H +λI,并且λ> 0确定阻尼的“强度”,它是一个标量参数。因此,将Bv公式化为Bv =(H +λI)v = Hv +λv。实际上,基本的Tikhonov阻尼方法在训练RNN方面并不好。由于RNN的复杂结构,即使在很小的距离下,参数空间中某些方向上的局部二次逼近也可能非常不精确因此,提出了结构阻尼,提高系统的鲁棒性。下面介绍具有结构阻尼的HF方法。 令e(x,θ)表示θ的向量值函数,该函数可在计算f(x,θ)时解释为中间量,其中f(x,θ)是目标函数。 例如,e(x,θ)可能包含的激活函数
神经网络中某些隐藏层(例如RNN)。 结构阻尼可以定义为:
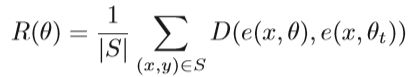
其中D是距离函数或损失函数。 通过惩罚e(x,θ)与e(x,θt)之间的距离,可以防止e(x,θ)的较大变化。 然后,阻尼局部目标可以写成
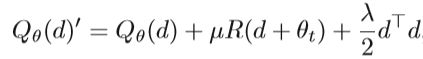
其中,μ和λ是两个要动态调整的参数。 d是第t次迭代的方向。此外,RNN中采用了许多二阶优化方法。 例如,提出了基于拟牛顿的优化和L-BFGS训练RNN。为了使基于惩罚的阻尼方法更好地工作, Levenberg-Marquardtstyle启发式方法用于直接调整λ。 方法描述如下:
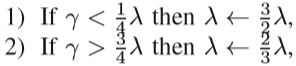
其中γ是具有以下形式的“还原率”:
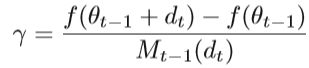
Sub-sampling
由于可以使用子采样Hessian矩阵处理大规模数据,它们使用了随机梯度或精确梯度。 这些方法使用Bt=∇2Stf(θt)作为Hessian近似,其中St是样本的子集。 意味着可以在每次迭代中节省大量计算。
Preconditioning
预处理可用于简化优化问题。 例如,预处理可以加速CG方法。 发现对角矩阵特别有效,可以使用以下预处理器:
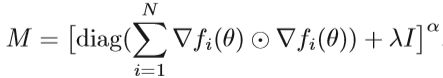
指数α选择小于1
B. Optimization in Reinforcement Learning
强化学习(RL)是机器学习的重要研究领域,使用深度强化学习在学习复杂的行为技能方面取得了巨大的成功,并解决了高维原始感知状态空间中具有挑战性的控制任务。 它通过试错机制与环境互动,并通过最大化累积奖励来学习最佳策略。它是基于惩罚和奖励的,与传统的机器学习不同。
首先介绍我们RL的几个概念,如下所示:
1)Agent(代理或者叫智能体):根据外部环境的状态采取不同的行动,并根据外部环境的收益调整策略。
2)Environment(环境):代理外部的所有事物都会受到代理动作的影响。 它可以更改状态并向代理提供奖励。
3) State s(状态): 对环境的描述。
4) Action a(行为):对代理行为的描述。
5) Reward rt(st−1,at−1,st)(奖励): 在时间t的及时返回值。
6) Policy π(a|s)(策略): 代理s根据当前状态决定动作a的功能。
7) State transition probability p(s′|s,a)(状态转移概率):在代理基于当前状态s选择动作a之后,环境在下一刻将转换为状态s’的概率分布。
8) p(s′,r|s,a):代理转变为状态s’并获得奖励r的概率,其中代理处于状态s并选择动作a。
加入一张图片方便理解:
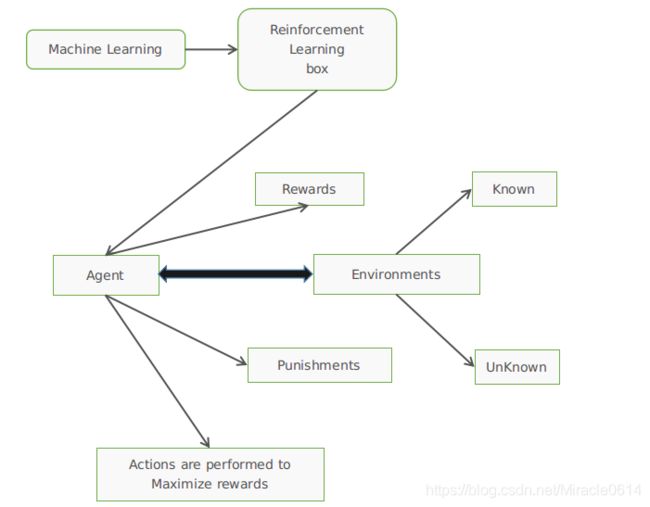
可以通过马尔可夫决策过程(MDP) 描述许多强化学习问题,其中S是状态空间,A是动作空间,P是状态转移概率函数,r是奖励函数,并且γ是折扣因子0 <γ<1。每次代理都接受一个状态,并根据策略从一个动作集中选择一个动作。MDP简单说就是一个Agent采取Action,从而改变自己的状态(State)获得奖励(Reward),与环境(Environment)发生交互的循环过程。
MDP 的策略完全取决于当前状态(Only present matters),这也是马尔可夫性质的体现代理从环境接收反馈,然后进入下一个状态。 强化学习的目的是找到一种策略,使我们能够获得最大的γ折扣累积奖励。 收益的计算公式为:
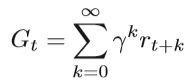
根据MDP问题的已知与未知,强化学习分为两类。 一种是基于模型的强化学习,它了解整个模型的MDP(包括转移概率P和奖励函数r),另一种是MDP未知的无模型方法。 在后一种方法中需要系统的探索。其中最常用的值函数是状态值函数:
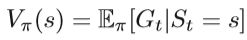
上式是从状态s执行策略π的预期收益。
状态作用值函数也是必不可少的,它是在状态s和策略π下选择作用a的预期收益,
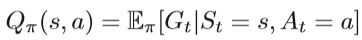
当前状态s的值函数可以通过下一状态s’的值函数来计算。Vπ(s)和Qπ(s,a)的Bellman方程描述为:
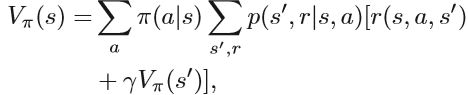
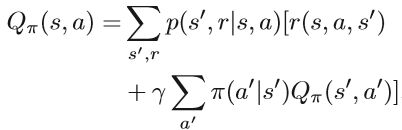
基于价值函数的强化学习方法很多。 它们被称为基于价值的方法,在RL中起着重要作用。 例如,Q-learning和SARSA是使用时差算法的两种方法。 基于策略的方法是直接优化策略πθ(a | s)并通过梯度下降更新参数θ。actor-critic算法是一种结合策略梯度和时间差分学习的强化学习方法,它同时估计两个结构的参数:
1)The actor 是一个策略函数,它学习策略πθ(a | s)以获得尽可能高的回报。
2)The critic参考学习的价值函数Vφ(s),它估计当前策略的价值函数,即评估actor。
在actor-critic方法中,critic解决了预测问题,而actor则关注控制。
基于价值的方法,基于策略的方法和actor-critic方法的概述如下:
1)基于价值的方法:它需要计算价值函数,并且通常得到一个确定的策略。
2)基于策略的方法:它在不根据值函数选择动作的情况下优化了策略π。
3)actor-critic批判方法:将上述两种方法结合起来,同时学习策略π和状态值函数。
深度强化学习(DRL)结合了强化学习和深度学习,可在RL框架中定义问题并优化目标,并使用深度学习技术解决诸如状态表示和策略表示之类的问题。DRL在许多具有挑战性的控制任务中都取得了巨大的成功,并使用DNN来表示控制策略。 对于神经网络训练,通常选择简单的随机梯度算法或其他一阶算法,但是这些算法在权重空间的探索上效率不高,这使得DRL方法通常需要几天的时间来训练。 因此,提出了一种分布式方法来解决这个问题,其中并行的角色学习者在训练过程中具有稳定作用。
C. Optimization in Meta Learning
元学习是机器学习领域中流行的研究方向。 它解决了学习怎样学习的问题。 在过去的认知中,机器学习的研究是首先获取特定任务中的大量数据,然后使用这些数据来训练模型。 但是如果只需几个训练样本就可以很好地处理新任务,这比传统的机器学习方法要有效得多。 元学习的目标是设计一个模型,该模型可以使用尽可能少的样本来很好地训练新任务,而不会过度拟合。 适应新任务的过程本质上是元测试中的学习过程,但仅限于来自新任务的有限样本。 元学习方法在监督学习中的应用可以解决小样本学习问题,通常将元学习概括为三个方向:基于度量的方法,基于模型的方法和基于优化的方法。
在本小节中,我们重点介绍基于优化的元学习方法。 在元学习中,通常有一些任务具有足够的训练样本,而新任务只有少数训练样本。主要思想可以描述如下:在元训练步骤中,从包含(Dtrainτ,Dtestτ)的总任务集T中采样任务τ。 对于任务τ,用训练样本Dtrainτ训练和更新优化器参数θ,用测试样本Dtestτ更新元优化器参数φ。 采样任务和更新参数的过程会重复多次。 在元测试步骤中,已训练的元优化器用于学习新任务。
由于元学习的目的是实现快速学习,因此关键是要在优化中更准确地进行梯度下降。 在某些元学习方法中,优化过程本身可以视为学习预测梯度的学习问题,而不是确定的梯度下降算法。 具有原始梯度作为输入和预测梯度作为输出的神经网络通常用作元优化器。 使用来自其他任务的训练和测试样本来训练神经工作,并将其用于新任务。 训练过程中的参数更新如下:
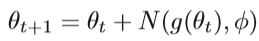
其中θt是迭代t次的模型参数,N是具有参数φ的元优化器,用于学习如何预测梯度。 训练后,根据测试样本中的损耗值更新元优化器N及其参数φ。 实验证明,学习神经优化器比自适应随机梯度优化方法更具优势。 由于反向传播中的梯度更新与长短期记忆(LSTM)中的单元状态更新之间的相似性,LSTM通常用作元优化器。关于LSTM模型的相关知识感兴趣的可以自行学习。
模型不可知的元学习算法(MAML) 是另一种用于元学习的方法,它适用于不同的学习问题,包括分类,回归和强化学习。模型不可知算法的基本思想是同时开始多个任务,然后获取不同任务的综合梯度方向,从而学习一个通用的基础模型。 主要过程可以描述如下:在元训练步骤中,从总任务集T中提取包含(Dtraini,Dtesti)的多个任务批τi。对于所有τi,训练并更新参数θ 'i与通过Dtraini:
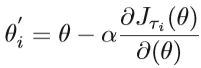
其中α是训练过程的学习率,Jτi(θ)是任务i中训练样本为Dtraini的损失函数。 在训练步骤之后,在相应任务的测试样本Dtesti上使用这些参数θ’i的合成梯度方向来更新参数θ:
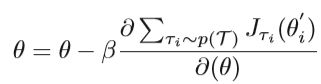
其中β是测试过程的元学习速率,Jτi(θ)是具有测试样本Dtraini的任务i中的损失函数。重复多次训练以获得好的初始参数θ。MAML不会为元学习引入其他参数,也不需要特定的学习器体系结构。 该方法的发展对基于优化的元学习方法具有重要意义。
D. Optimization in Variational Inference
在机器学习中,有许多概率模型具有复杂的结构和难以理解的后验,因此使用了一些近似方法,例如变分推断VI和马尔可夫链蒙特卡洛(MCMC)采样。 变分推断广泛用于近似贝叶斯模型的后验密度,将复杂的推理问题转换为高维优化问题。与MCMC相比,变分推断更快,更适合处理大规模数据。回顾一下VI的原理,VI通过尝试最小化潜在的因式分布和真实后验之间的KL差异来逼近真实后验。
令Z = {zi}表示模型中所有潜在变量和参数的集合,而X = {xi}是所有观测数据的集合。 X和Z的联合分布为p(Z,X)= p(Z)p(X | Z)。 在贝叶斯模型中,应计算后验分布p(Z | X)以作进一步推断。我们需要做的是用属于约束分布族的分布q(Z)近似p(Z | X)。 目的是使两个分布尽可能相似。 变分推论选择KL散度来度量两个分布之间的差异,即最小化q(Z)和p(Z | X)的KL散度。 这是q和p之间的KL散度的公式:
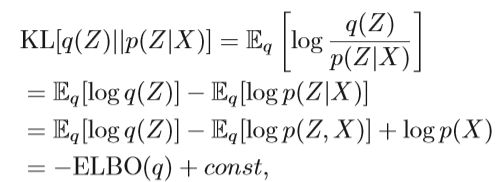
其中logp(X)被常量(const)替换,因为我们只对q感兴趣。 通过上述公式,可以知道KL散度很难优化,因为它需要知道我们试图近似的分布。 另一种方法是最大化证据下界(ELBO),这是观察值的边际概率的对数的下界。 我们可以得到ELBO的公式为
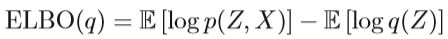
VI可以视为一个优化问题,目的是使ELBO最小化。 一种直接方法是使用坐标上升来解决此优化问题,称为坐标上升变分推断(CAVI)。 CAVI迭代优化平均场变异密度的每个因子,同时保持其他因子固定,变分分布q具有平均场的结构,即q(Z)= ∏ i = 1 M ∏ i = 1 M \prod ^{M}_{i=1}∏i=1M ∏i=1M∏i=1M qi(zi)。 在此假设下,可以通过一些推导将分布q引入ELBO,并获得以下公式,具体见Algorithm 8 :
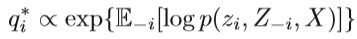

在传统的坐标提升算法中,处理大数据的效率非常低,因为每次迭代都需要计算所有数据, 随机优化使机器学习能够扩展到海量数据上。 通过将随机优化引入变分推断,提出了随机变量推论(SVI)。高斯过程(GP)是一种基于统计学习和贝叶斯理论的重要机器学习方法,有强大的泛化能力。然而,针对GP的精确解决方案的复杂性和存储要求很高,这阻碍了GP在大规模数据下的发展。本节介绍的随机变分推理方法可以在大规模数据集上推广变分推理,但只能应用于具有分解结构的概率模型。对于其观测值相互关联的GP,可以通过引入全局归纳变量作为变化变量来适应SVI。
E. Optimization in Markov Chain Monte Carlo
MCMC是一类采样算法,用于模拟难以直接采样的复杂分布。 是贝叶斯后验推断的实用工具。 传统和常见的MCMC算法
包括 Gibbs sampling, slice sampling,Hamiltonian Monte Carlo (HMC) (HMC),Reimann manifold variants 等。本节以HMC为例,介绍MCMC中的优化。 HMC的瓶颈在于,对于大型数据集梯度计算成本很高。首先介绍HMC的派生,考虑可以从后验分布中采样的随机变量θ,
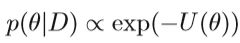
其中D是观测值集合,U是势能函数,具有以下公式:
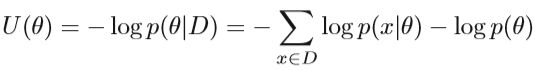
在HMC中,从 Hamiltonian dynamic中引入了一个独立的辅助动量变量r。 Hamiltonian function以及θ和r的联合分布描述为:
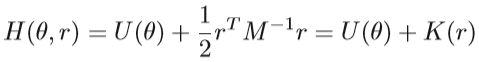
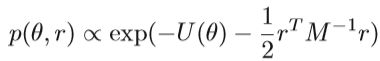
其中M表示质量矩阵,K(r)是动能函数。 通过模拟Hamiltonian动力学系统得出HMC采样过程,多写一句,其实上式的H(θ,r) 就是物理学中的动能+势能=总能量。
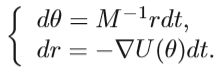
Hamiltonian方程描述了物体在某个时刻的运动状态,这个时间点时连续变量,为了模拟Hamiltonian在动力学上的数值运算,有必要将时间离散化从而实现Hamiltonian的近似估计,基本的方法是在T时间间隔内,分割成一系列长度为 ε ε \varepsilon ε εε的小区间,如果将 ε ε ε处理成很小,这样时间间隔T也是近似连续的。
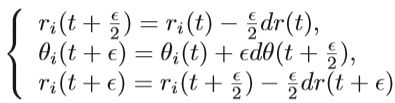
为了提高效率,使用了随机梯度法来计算∇U(θ),并从D均匀小批样采样,从而降低了计算成本。 但是,以小批量而不是完整数据集计算的梯度会引起噪声。 根据中心极限定理,该噪声梯度可近似为:
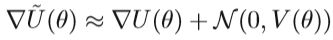
梯度噪声服从正态分布,其协方差为V(θ)。 如果我们将∇U(θ)用上式替换,则Hamiltonian dynamics将变为:
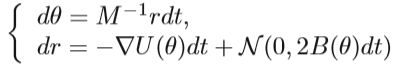
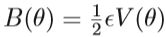
由于动力系统的离散化会引入噪声,因此,Metropolis-Hastings(MH)校正步骤应在跳过步骤之后完成。 这些MH步骤需要在每次迭代中进行大量计算。 除此之外,HMC的随机梯度变量中存在不正确的平稳分布。 因此,对Hamiltonian动力学进行了进一步的修改,实现不变分布并消除MH阶跃。 具体来说,将摩擦项添加到动量更新的动力学过程中。
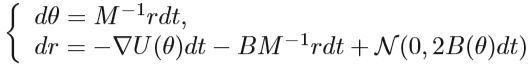
引入的摩擦项有助于降低动能更新阶段的总能量H(θ,r)并减弱噪声的影响。 此外,HMC对路径长度(步数)L和步长 ε ε ε等超参数高度敏感,最好的方法是优化这两个参数,而不是手动调参:
1) Path Length L: L太小,则所得采样点之间的距离将非常接近; 如果L太大,则生成的采样点将循环返回。Matthew et al提出了HMC方法的扩展,称为No-U-Turn采样器(NUTS),该方法使用递归算法有效地生成一组可能的独立样本,并通过自动区分回溯来停止模拟。 无需手动设置步骤参数L。 在具有多个离散变量的模型中,NUTS能够自动选择轨道长度,从而使其能够生成比原始HMC更多的有效样本并更有效地执行。
2) Adaptive Step Size ε ε ε: 如果 ε ε ε太小,更新将变慢,计算成本会很高; 如果 ε ε ε太大,则拒绝率会很高,从而导致无用的更新。可以在HMC中使用对偶平均算法的消失适应。 具体来说,在双重平均方法中采用统计量Ht =δ-αt,其中δ是期望的平均接受概率,而αt是迭代t的当前 Metropolis-Hasting接受概率。 统计Ht的期望h( ε ε ε)定义为:
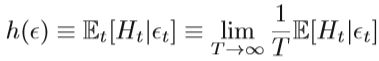
其中 ε ε ε是跨越式积分器中迭代t的步长。 为了满足h( ε ε ε)≡Et [Ht |ǫt] = 0,我们可以导出 ε ε εt+1 = ε ε ε-ηtHt。 通过消失的自适应算法进行调整 ε ε ε,可以确保Metropolis的平均接受概率接近固定值。
除了二阶SGHMC之外,随机梯度Langevin动力学(SGLD)是结合随机优化的一阶Langevin动力学技术。 SGLD和SGHMC的有效变体仍然有效。
挑战和开放性问题
A. Challenges in Deep Neural Networks
1) Insufficient Data in Training Deep Neural Networks
通常,深度学习基于大数据集和复杂模型。 需要大量的训练样本才能达到良好的训练效果。 但是在某些特定领域,很难找到足够数量的训练数据。 如果我们没有足够的数据来估计神经网络中的参数,则可能导致高方差和过度拟合。 神经网络中有一些技术可用于减少方差。 向目标添加L2正则化是降低模型复杂度的一种方法。 另一种常见的方法是 dropout 。 在训练过程中,允许每个神经元以p的概率停止工作,这可以防止某些神经元之间的协同作用。 M个子网可以像装袋一样通过多次放入和放回进行采样。 输出层的每个预期结果计算如下:
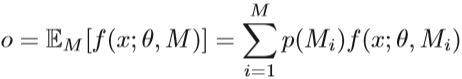
其中p(Mi)是第i个子网的概率。dropout可以防止过拟合并提高泛化能力,但缺点是增加了训练时间。
由于DNN的复杂性,不仅过度拟合而且某些训练细节也会影响模型的性能。 SGD中学习速率和迭代次数的选择不当将使模型无法收敛。 此外,采用不合适的神经网络构建黑匣子可能导致训练无法继续进行,当数据不足时,这些影响会更大。
在数据不足的情况下,迁移学习技术可用于构建网络。 它的想法是,经过某些修改和改进,可以从其他数据源训练的模型在相似的目标领域中重复使用,从而极大地缓解了因数据集不足而引起的问题。 此外,还可以避免有效地过度拟合并总体上获得更好的性能。但是数据之间要保证相关性。
元学习方法可用于系统地学习参数初始化,从而确保训练始于合适的初始模型。 在具有相似数据源进行训练的模型的前提下,转移学习和元学习可以克服新数据源中训练数据不足所造成的困难,但是这些方法通常会引入大量参数或复杂的参数调整机制,因此,使用不足的数据来训练DNN仍然是一个挑战。
2) Non-convex Optimization in Deep Neural Network:
凸优化具有良好的属性,但是,许多机器学习问题被表述为非凸优化问题。 例如,DNN中几乎所有优化问题都是非凸的。 非凸优化是优化问题中的难题之一。 与凸优化不同,在非凸问题中的可行域中可能存在无数的最优解。 搜索全局最优值的算法的复杂性是NP-hard。
解决非凸优化问题的方法可以大致分为两种。 一种是将非凸优化问题转化为凸优化问题,然后使用凸优化方法。 另一种是使用一些特殊的优化方法直接求解非凸函数。 从机器学习的角度,有一些工作总结了解决非凸函数的优化方法。
1)Relaxation method:有许多松弛技术,称为αBB凸松弛,该方法在每一步都使用凸松弛来计算区域的下限。 凸松弛法已在许多领域中使用。
2) Non-convex optimization methods:包括投影梯度下降,交替最小化,期望最大化算法和随机优化及其变体。
B. Difficulties in Sequential Models with Large-Scale Data
在处理大规模时间序列时,通常的解决方案是使用随机优化,以小批量处理数据或利用分布式计算来提高计算效率。对于顺序模型,对序列进行分段会影响相邻时间索引上数据之间的依赖性。如果序列长度不是小批量大小的整数倍,则通常的操作是将一些从先前数据中采样的项目添加到最后一个子序列中。此操作将在训练模型中引入错误的依赖性。因此,分析获得的近似解与精确解之间的差异是值得探索的方向。特别地,在RNN中,也容易发生梯度消失和梯度爆炸的问题。到目前为止,通常可以通过LSTM和GRU的特定交互模式或梯度裁剪解决。更好的解决RNN问题的合适解决方案仍然值得研究。
C. High-Order Methods for Stochastic Variational Inference
高阶优化方法利用曲率信息,从而快速收敛。 尽管很难计算和存储黑森州矩阵,但是随着研究的发展,黑森州矩阵的计算取得了长足的进步,并且二阶优化方法变得越来越多。最近,随机方法也被引入到二阶方法中,将二阶方法扩展到大规模数据。本文介绍了一些有关随机变分推断的工作。这使得变分推理能够处理大规模数据。一个自然的想法是,我们是否可以将二阶优化方法(或更高阶)纳入随机变异推断中。
D. Stochastic Optimization in Conjugate Gradient
随机方法在处理大规模数据时表现出强大的功能,尤其是对于一阶优化而言。然后相关专家学者也将此随机思想引入了二阶优化方法,并取得了良好的效果。共轭梯度法是一种很好的算法,具有一阶和二阶优化方法的优点。共轭梯度的标准形式不适用于随机近似。通过使用快速的Hessian梯度积,随机方法也被引入到共轭梯度中,其中一些数值结果证明了该算法的有效性。随机共轭梯度法的另一种形式采用方差减少技术,并且只需几次迭代即可快速收敛,并且在运行过程中需要较少的存储空间。共轭梯度的随机形式是一种潜在的优化方法,仍然值得研究。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()