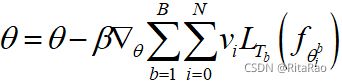元学习论文解读 | How to train your MAML , In ICLR 2019.

目录

motivation

contribution

核心内容

Related Work

Problems of MAML

训练不稳定性

二阶导数代价

缺少批处理归一化统计量的积累

共享(跨步)批处理规范化偏差

共享内部循环(跨步和跨参数)学习率

固定的外环学习率

Stable,automated and improved MAML: MAML++

梯度不稳定性→多步损失优化(MSL)

二阶导数成本→导数退火DA

缺少Batch Normalization统计信息累积→Per-Step Batch Normalization运行统计信息（BNRS）

共享（跨步骤）Batch Normalization偏差→Per-Step Batch Normalization权重和偏差（BNWB）

共享的inner loop学习率（跨步和跨参数）→学习每层每步学习率和梯度方向（LSLR）

固定outer loop学习率→元优化器学习率的余弦退火（CA）：

Results

总结

---

motivation

MAML是目前通过元学习进行小样本学习的最佳方法之一。它很简单,非常强大,但是,它有各种各样的问题：①训练过程中的不稳定性,②二阶导数一阶近似代价（限制模型的泛化性能）,③批处理规范化使用当前批处理的统计信息 ④内部循环及外部循环中固定的学习率（固定意味着更复杂的超参数调优）

contribution

本文基于上述问题提出对MAML的各种改进，不仅使系统稳定，而且大大提高了MAML的泛化性能、收敛速度和计算量，称之为MAML++。

核心内容

Related Work

基于度量的元学习方法（原型网络、匹配网络等）;Meta-LSTM;Meta-SGD

Problems of MAML

训练不稳定性

优化外部回路涉及到通过一个展开的内部回路反向传播导数，内部回路由相同的网络组成多次，同时模型架构是一个标准的没有跳转连接的4层卷积网络，没有任何跳转连接意味着每个梯度必须通过每个卷积层多次，也就是乘相同的参数集多次。在经过多次反向传播后，未展开网络的深度结构大和缺少跳跃连接分别会导致梯度爆炸和梯度消失问题。

二阶导数代价

MAML使用一阶近似来加速过程，但是可能会对最终的泛化误差产生负面影响。在reptile中在基础模型上应用标准SGD，然后在N步之后从初始化参数向基础模型的参数迈进一步，但只在某些情况下超过MAML。在不牺牲泛化性能的情况下减少计算时间的方法还没有被提出。

缺少批处理归一化统计量的积累

将当前批处理的统计信息用于批处理规范化效率较低，因为学到的偏差须适应各种不同的平均值和标准偏差。若使用积累的运行统计信息，它最终将收敛到某个全局平均值和标准偏差。

注：归一化特征将导致更平滑的优化场景(Santurkar et al., 2018)

共享(跨步)批处理规范化偏差

批处理规范化偏差不会在内部循环中更新，在基础模型的所有迭代中使用相同的偏差。这样做隐含地假设在整个内部循环更新过程中所有的基础模型都是相同的。这是错误的，因为在每次内部循环更新时，会实例化一个与前一个不同的新的基础模型（经过任务适应得到任务特定的模型）。

共享内部循环(跨步和跨参数)学习率

影响泛化和收敛速度(在训练迭代方面)的一个问题是对所有参数和所有更新步骤使用共享学习率的问题。这样做会带来两个主要问题——需要做多个超参数搜索，以找到一个特定数据集的学习率;计算成本可能很高。

固定的外环学习率

MAML中使用具有固定学习率的Adam来优化元目标。使用阶跃函数或余弦函数对学习速率进行退火已被证明是在多种设置下实现先进的泛化性能的关键。因此使用静态学习率有可能降低了MAML的泛化性能和优化速度。固定的学习率也意味着须花费更多的时间调整。

Stable,automated and improved MAML: MAML++

梯度不稳定性→多步损失优化(MSL)

MAML是在完成对支持集的内部循环更新后，将基网络计算出的集损失最小化。本文提出在内部循环的每一步都考虑测试集的损失最小化，也就是说一个任务的经验风险是每步support set loss更新后query set loss的加权总和：

 

每一步的基网权值既可以直接(对于当前步的loss)和间接(来自后续步的loss)接收梯度。原始方法中基于反向传播，除了最后一步，每一步的基础网络权值都被隐式地优化，导致许多不稳定性问题，使用多步骤丢失可以缓解这个问题。此外采用退火加权每步损失（i越大，vi越大）。

二阶导数成本→导数退火DA

MAML在整个训练阶段都采用了一阶近似，我们随着训练的进行对微分阶数进行退火。如在训练阶段的前50个epochs使用一阶梯度，然后在训练阶段的其余时间使用二阶梯度。

缺少Batch Normalization统计信息累积→Per-Step Batch Normalization运行统计信息（BNRS）

更好的替代方法是按步骤收集统计信息。要按步骤收集运行统计信息，需要实例化网络中每个批正则化层的N组运行平均值和运行标准偏差集（其中N是inner loop更新步骤的总数），并使用优化过程中采取的步骤分别更新running统计信息。per-step batch normalization方法应加快MAML的优化速度，同时潜在地提高泛化性能。

共享（跨步骤）Batch Normalization偏差→Per-Step Batch Normalization权重和偏差（BNWB）

在inner-loop更新过程中每步学习一组偏差。这样做意味着Batch Normalization将学习特定于在每个集合处看到的特征分布的偏差，这将提高收敛速度，稳定性和泛化性能。

共享的inner loop学习率（跨步和跨参数）→学习每层每步学习率和梯度方向（LSLR）

Meta-SGD方法证明了学习基础网络中每个参数的学习率和梯度方向可以提高系统的泛化性能，但参数数量、计算开销将增加。因此，本文改为学习网络中每一层的学习率和方向，以及随着基础网络的逐步适应而学习不同的学习率。学习每层而不是每个参数的学习率和方向应该减少所需的内存和计算，同时在更新步骤中提供更多的灵活性。

固定outer loop学习率→元优化器学习率的余弦退火（CA）：

余弦退火调度应用于元模型的优化器（即元优化器）。退火学习率可使模型更有效地拟合训练集，结果可能会产生更高的泛化性能。

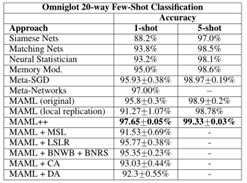
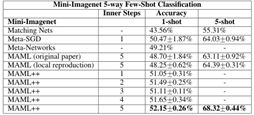
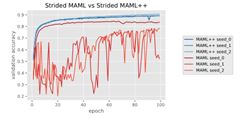
Results

     

 ​​​​​​​

总结

感觉做了很多角度的优化，单个角度的效果不是特别明显，组合拳虽然有效果，牺牲了很多计算量和内存量，单步目标损失优化稳定性能提升很多，但计算量是个问题。